経済統計の使い方
統計初心者の社会人向けに、経済データの解説をしています。「まとめページ」をご覧くだされば、全体的な内容がわかると思います。
R

【R】最小二乗法の推計と予測法を徹底解説｜lm関数

  /
かえで

Rで、最小二乗法は　lm(y ~ x1+x2) と指定します。

さくら

なぜコマンド名は　lm　なんですか？

かえで

linear models （線形モデル）の略です。

この記事では、Rを使った簡単な最小二乗法の推定法を説明します。lm関数を使うと最小二乗法が推定でき、summary関数で結果が見られます。predict関数を使うと予測ができます。

経済統計の使い方では、統計データの入手法から分析法まで解説しています。

【R】Rのまとめ 経済統計の使い方では、統計データの入手法から分析法まで解説しています。 https://officekaisuiyoku.com...
Contents
  1. データフレームの作成
  2. 最小二乗法
  3. 予測
  4. 最小二乗法による係数の求め方

データフレームの作成

cp <- data.frame("GDP95"=c(311988.0 ,320726.7 ,330912.0 ,338991.9 ,352924.7 ,368211.9 ,379845.5 ,398927.2 ,424294.1 ,444876.0 ,469567.2 ,480855.2 ,483022.6 ,485298.3 ,489588.5 ,504827.3 ,521364.8 ,522220.9 ,518706.4 ,520765.6 ,539161.1 ,532444.5 ,541200.0 ), "CP95"=c(174234.2 ,176912.6 ,184665.6 ,189188.9 ,194156.2 ,201565.5 ,208975.1 ,217229.6 ,229047.3 ,238716.3 ,249355.1 ,257141.5 ,261717.7 ,266382.5 ,272215.1 ,279472.3 ,286514.5 ,282965.3 ,286104.1 ,288346.2 ,290585.4 ,294798.9 ,298974.3 ))
Copy

実質GDPと実質民間最終消費支出のデータを入力し、cpというデータフレームに格納しました。

matplotコマンドでグラフを描くと以下のようになります。1が実質GDP,２が実質民間最終消費です。

matplot(cp,type="l")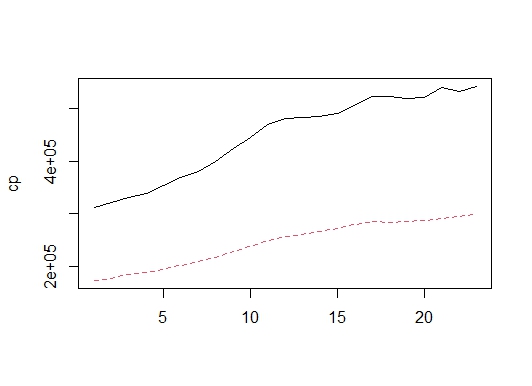
Copy

最小二乗法

最小二乗法のコマンドは lm です。被説明変数を最初に置き、～マークの次に説明変数を置きます。2つ以上説明変数がある場合は、＋記号を使って並べます。 y ~ x1 + x2 のような形です。

被説明変数がCP95、説明変数がGDP95の場合は以下の式になります。推計結果はresultという名前にしていますが、名前は任意に決められます。

result<−lm(GP95 GDP95,data=cp)

結果を見るには、summary関数を使います。summary(result)で以下の結果が表示されます。

 summary(result)

Call:
lm(formula = CP95 ~ GDP95, data = cp)

Residuals:
   Min     1Q Median     3Q    Max 
 -7565  -2393    411   2672   4505 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) 3.845e+03  4.316e+03   0.891    0.383    
GDP95       5.390e-01  9.514e-03  56.646   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 3531 on 21 degrees of freedom
Multiple R-squared:  0.9935,	Adjusted R-squared:  0.9932 
F-statistic:  3209 on 1 and 21 DF,  p-value: < 2.2e-16
Copy

最小二乗法の推定結果を検討するために必要な、係数、ｔ値、p値、Ｆ値、自由度修正済み決定係数などが入手できます。推定された式は以下です。

CP95＝3.845e+03+5.390e−01×GDP95+e

指数表示を普通の表示に直すと以下の通りです。

CP95＝3845+0.5390×GDP95+e

定数項である3845に対するt値は0.89でp値は0.383、GDP95に係る係数の0.539に対するt値は56.646で、ｐ値は2e-16（ほぼゼロ）です。F値は自由度（1，21）で3209で対応するp値は 2.2e-16になります。自由度修正済み決定係数は0.9932となります。

そのほかにも、様々な出力ができます。推定結果をresultとした場合の表です。

関数内容例
fitted推定値result$fitted
predict予測値result$predict,fitted(result)
print簡単な結果の要約print(result)
summary結果の要約summary(result)
plot回帰診断plot(result)

推計値は、result$fittedで得ることが出来ます。fitted(result)とすると、推定値が表示されます。

fitted(result)
       1        2        3        4        5        6        7        8 
171992.1 176701.9 182191.3 186546.0 194055.1 202294.1 208564.1 218848.2 
       9       10       11       12       13       14       15       16 
232519.8 243612.4 256919.8 263003.5 264171.6 265398.1 267710.3 275923.3 
      17       18       19       20       21       22       23 
284836.3 285297.6 283403.5 284513.3 294427.6 290807.7 295526.5
Copy

printコマンドでは、式の形と係数が表示されます。

> print(result)

Call:
lm(formula = CP95 ~ GDP95, data = cp)

Coefficients:
(Intercept)        GDP95  
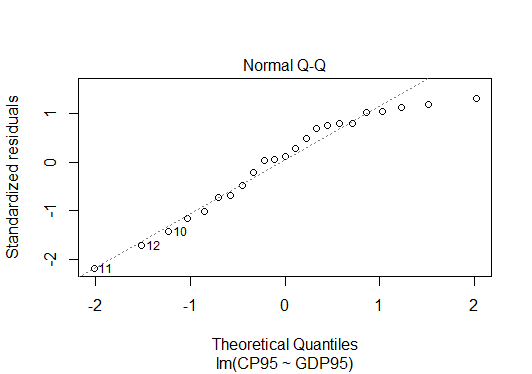
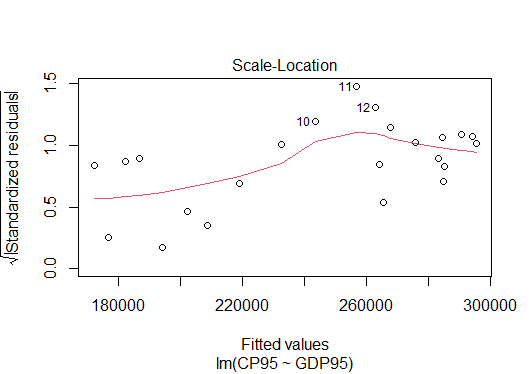
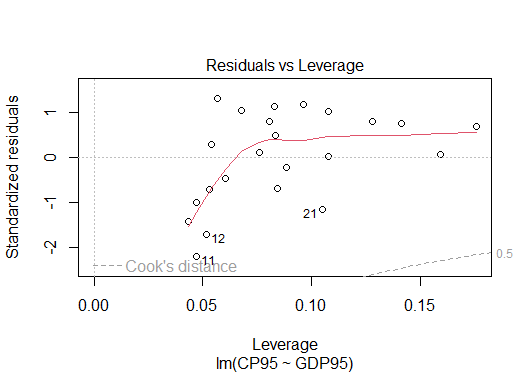
   3845.475        0.539
Copy

回帰診断は、plot(result)で実行できます。4種類のグラフがリターンキーを押すと次々に出てきます。

  > plot(result)
Hit <Return> to see next plot: 
Hit <Return> to see next plot: 
Hit <Return> to see next plot: 
Hit <Return> to see next plot: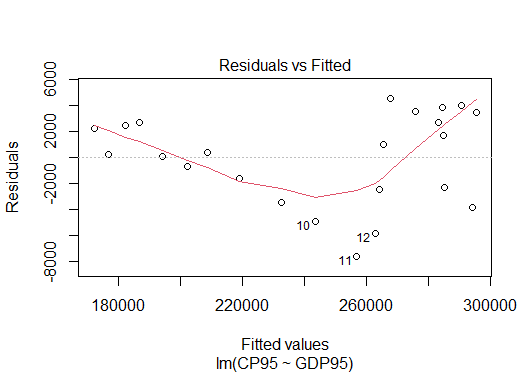
Copy

予測

次に予測の方法を説明します。推定した方程式が以下の場合で説明します。

CP95＝3845+0.5390×GDP95+e

右辺のGDP95に新たなデータを入れ、誤差項はゼロとすると、CP95の予測値が得られます。最小二乗法による予測は、右辺にあるGDP95 はあらかじめ何らかの形で予測しておかないとできません。

現在データは23期目まであるので、24期目のGDP95が3％増えたとして、それに対応したCP95を予測します。まず新たなデータフレームとしてcpをコピーしてcpfを作成し、24期目のデータを23期目の３％増加したものとします。

> cpf <- cp
> cpf[24,1] <- cpf[23,1]*1.03
Copy

この新たなデータに予測するためのpredcit関数を適用すると予測ができます。lm関数の時はdata＝としてデータフレームを指定しましたが、predict関数ではnewdata=とするところがポイントです。予測値をCP95fという名前でデータフレームcpfに格納します。

 cpf$CP95f <- predict(result,newdata=cpf）
Copy

予測値を含めたデータが以下のように作成されました。23期より前は推定値、24期が予測値になります。

> cpf
      GDP95     CP95    CP95f
1  311988.0 174234.2 171992.1
2  320726.7 176912.6 176701.9
3  330912.0 184665.6 182191.3
4  338991.9 189188.9 186546.0
5  352924.7 194156.2 194055.1
6  368211.9 201565.5 202294.1
7  379845.5 208975.1 208564.1
8  398927.2 217229.6 218848.2
9  424294.1 229047.3 232519.8
10 444876.0 238716.3 243612.4
11 469567.2 249355.1 256919.8
12 480855.2 257141.5 263003.5
13 483022.6 261717.7 264171.6
14 485298.3 266382.5 265398.1
15 489588.5 272215.1 267710.3
16 504827.3 279472.3 275923.3
17 521364.8 286514.5 284836.3
18 522220.9 282965.3 285297.6
19 518706.4 286104.1 283403.5
20 520765.6 288346.2 284513.3
21 539161.1 290585.4 294427.6
22 532444.5 294798.9 290807.7
23 541200.0 298974.3 295526.5
24 557436.0       NA 304276.9
Copy

実績値と予測値のグラフを描くと以下のようになります。実線が実績値、点線が推定値（実績がある23期まで）と予測値（24期）です。

matplot(cpf[,2:3],type="l")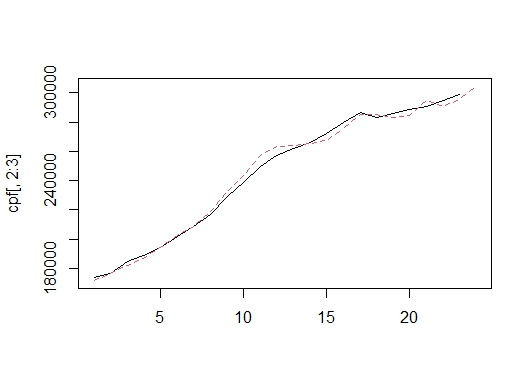
Copy

最小二乗法による係数の求め方

lm関数を使えば、係数は簡単に計算されます。実際にどのような手順で作成されているかを考えると以下の式になります。重回帰の分析の場合にも使えます。

yは被説明変数のベクトル、Xは、定数項を表す要素が1の列と、説明変数の列を合わせた行列です。説明変数が1つの場合は2列で、説明変数が増えると列が増えます。

行列の計算式として、Xを例にとると逆行列はsolve(X)、行列の積は%*％、行と列を入れ替えた転置行列　X′　はt (X)で表します。

β=(X′X)−1X′y

> y  <- cp$CP95 
> x   <- cbind(1, cp$GDP95)  
> solve( t(x) %*% x ) %*% t(x) %*% y  
　　　　 [,1]
[1,] 3845.4748610
[2,]    0.5389523
Copy

計算の結果、定数項が3845.4748610、GDP95 に係る係数が0.5389523と計算されます。

R
RELATED POST

COMMENT

メールアドレスが公開されることはありません。 ※ が付いている欄は必須項目です

CAPTCHA