説明変数が外生変数(ほかの変数から影響を受けない)であることが最小二乗法が最適な推定値になる条件ですが、それが満たされていない場合です。説明変数に内生性があるというのは、説明変数と誤差項に相関がある場合です。
説明変数に内生性がある場合は、操作変数を使うことが有効です。操作変数を使うことで、内生性の問題は解決できます。ただ、適切な操作変数を探すことが容易でないのが問題です。
経済統計の使い方では、統計データの入手法から分析法まで解説しています。

説明変数の内生性
説明変数に内生性があるとは、説明変数が誤差項と相関している場合です。最近では、因果関係の推定の際に、必要な変数を落とした場合(脱落変数)に生じることが問題になっています。説明変数と誤差項に相関が生じる原因として以下の例があります。
- 需要曲線と供給曲線の推定
- 同時方程式モデル
- 計測誤差がある場合
- 欠測値がある場合
需要曲線と供給曲線
最初に問題にされたのは、需要曲線と供給曲線の推計です。需要曲線、供給曲線は以下のように書けます。
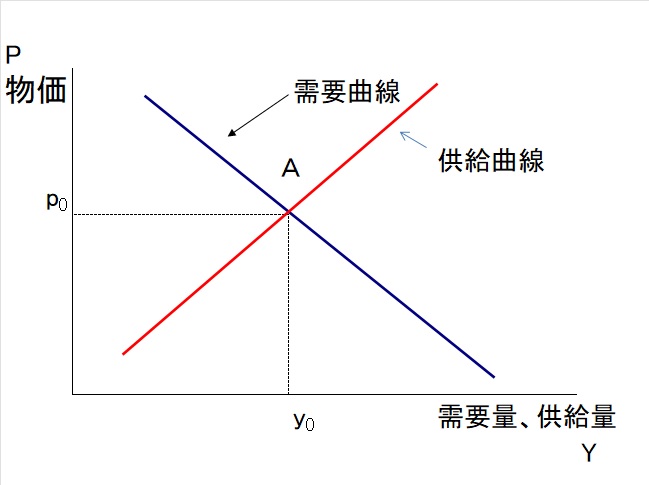
需要曲線の傾きは負、供給曲線の傾きは正となります。
価格と供給量のデータを得ることはできますが、取引が成立した点のデータしかわかりません。価格$P_i$を被説明変数、需要量、供給量$Y_i$を被説明変数とすると、以下の式が成り立ちます。推計上難しいのは、需要曲線は右下がりなので$\beta^d$は負、供給曲線は右上がりなので$\beta^s$は正という結果が出ないといけないことです。しかしデータは同じですから、異なる2つの結果は出てきません。両方が混ざった$\beta$が推定されることになります。
$需要曲線 P_i=\alpha^d+\beta^d Y_i +e^d_{i}$
$ 供給曲線 P_i=\alpha^s +\beta^s Y_i+e^s_{i} $
また、この推計式は説明変数と誤差項が相関しているケースでもあります。取引が成立するのは、需要と供給の価格が等しくなった時なので、以下が成り立ちます。
$\alpha^d+\beta^d Y_i +e^d_{i}=\alpha^s +\beta^s Y_i+e^s_{i} $
これを$Y_i$について解くと以下の式になります。
$ Y_i= \dfrac{(e^d_i-e^s_i)-(\alpha^d – \alpha^s )}{\beta^d – \beta^s} $
説明変数$Y_i$は、誤差である$e^d_i$と$e^s_i$の影響を受けていることがわかります。
同時方程式モデル
計量経済モデルでが、ある式では説明変数、他の式では被説明変数になっている変数があります。こういう場合は、説明変数が内生変数となります。
消費関数と国民所得からなる、簡単なケインズモデルを考えてみます。
$C_i=a+bY_i+e_i$
$Y_i=C_i+I_i$
消費$C_i$の説明変数である国民所得$Y_i$は、他の変数から影響を受けない外生変数ではありません。以下のように、説明変数$Y_i$と誤差項$e_i$は相関しています。
$Y_i=a+bY_i+e_i+I$
$Y_i= \dfrac{a+e_i+I}{1-b}$
計測誤差
計測誤差がある場合は、$X_i$が確定的に決まらないことで、$Y_i$の回帰係数が小さ目に推定されます。理論モデルとして以下の式が成り立っているとします。
$Y_i=\alpha+\beta X_i+e_i$
ただ、$X_i$は入手することができず、観測誤差のある$X^*_i+u_i$しか入手することが出来ないとします。この場合、以下の式を推計することになります。
$ Y_i= \alpha+ \beta (X^*_i+u_i)+e_i=\alpha+ \beta X^*_i+ \beta u_i+e_i $
誤差には$\beta$が含まれているので、$\beta$と誤差に相関があることになります。
脱落変数がある場合
最近操作変数が頻繁に使われるようになったのは、脱落変数バイアス(Omitted variables bias:OVB)を除去するためです。
真の変数の関係が以下であるとします。
$Y_i=\alpha+\beta X_i + \gamma A_i +e_i$
しかし、変数$A_i$は観察することができず、$X_i$のみに回帰するしかないとします。また、$A_i$と$X_i$は相関しているとします。$A_i$を除いて推定すると、$A_i$は誤差に含まれることになり、$X_i$と誤差項は相関します。
また、$A_i$と$X_i$には以下の関係があるとします。
$A_i=a+ b X_i + u_i $
この式を真の関係の式に代入すると以下の式となります。
$ Y_i=\alpha+a + (\beta+b)X_i +e_i+u_i $
つまり、本来の係数は推計されずに$\beta+b$が推計されることになります。これが脱落変数バイアスと呼ばれるものです。
操作変数法
説明変数と誤差項に相関がある場合、最小二乗法による推定値は、不偏性も一致性もないものになります。しかし、操作変数法を使うことで、一致性のある推定ができます。
操作変数は、$e_i$と相関していないけれど、$X_i$と相関している変数のことです。
年収と就学年数の例
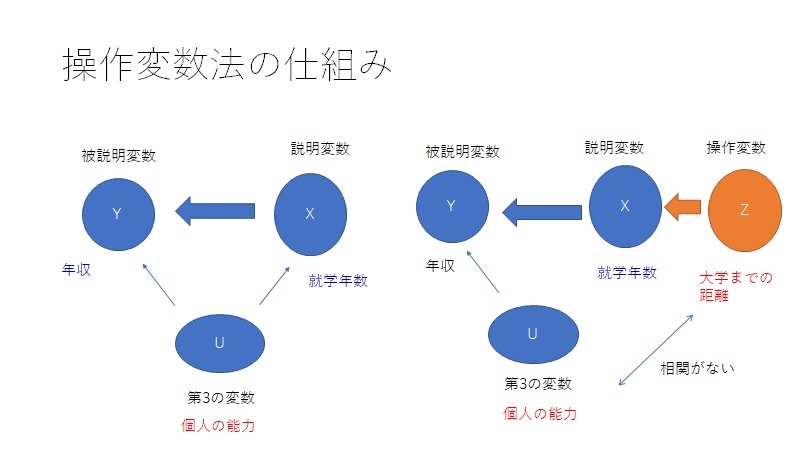
「脱落変数バイアス」がある場合について説明します。年収に与える影響は就学年数と個人の能力である場合です。しかし、個人の能力が推計できないとします。
個人の能力が脱落変数となり、もし、個人の能力が就学年数と相関がある場合、年収を就学年数だけで回帰すると脱落変数バイアスが生じてしまいます。
就学年数が個人の能力に影響を受けてしまうのが問題なので、個人の能力とは相関がないが、就学年数には影響がある変数を操作変数として捜します。
下の例では、大学までの距離を操作変数としています。大学までの距離は、個人の能力とは相関しないけれど、大学へ行きやすいことから就学年数を伸ばすことが考えられるためです。
通常の推計では就学年数は個人の能力の影響を受けますが、操作変数はその影響を断つ効果があります。
操作変数法の係数
まず、通常の最小二乗法の係数の推定値を単回帰の場合で表すと以下の式になります。
$ \beta=\dfrac{\Sigma \color{red}(X_i-\bar{X}) \color{black} (Y_i-\bar{Y})}{\Sigma \color{red}(X_i-\bar{X}) \color{black} (X_i-\bar{X})} $
操作変数法の係数の推定値は以下で表せます。分子と分母でそれぞれ一つずつ$X_i-\bar{X}$が$Z_i-\bar{Z}$に変わっているということです。
$ \beta_{IV}=\dfrac{\Sigma \color{red}(Z_i-\bar{Z})\color{black}(Y_i-\bar{Y})}{\Sigma \color{red}(Z_i-\bar{Z})\color{black}(X_i-\bar{X})}$
ただ、その意味するところは直感的にはわかりにくいです。
2段階最小二乗法
操作変数法は、2段階最小二乗法として計算されると考えるのがわかりやすいと思います。被説明変数を$Y_i$、説明変数を$X_i$、操作変数を$Z_i$とします。
まず、$X_i$に$Z_i$を回帰して$X_i$の理論値$\hat{X_i}$を作ります。
$ X_i= \alpha + \beta Z_i + u_i $
上記式の推計結果$\hat{X_i}$を$Y_i$に回帰させます。
$ Y_i= \gamma + \lambda \hat{X_i} + v_i $
この推定結果$\lambda$が操作変数法による推定値になります。
- 【時系列分析】課題3 ドリフト付きランダムウォーク
- 【時系列分析】課題2 グレンジャーの因果関係
- 【時系列分析】課題1 為替レートの予測
- 「回帰分析から学ぶ計量経済学」を使ったセミナーを行います(2024年3月8日)
- 正誤表 回帰分析から学ぶ計量経済学