【時系列分析】課題３　ドリフト付きランダムウォーク

ドリフト付きランダムウォーク

ドリフト付きランダムウォークとは、ランダムウォークの式に定数項（ドリフト項）を付けたものです。時間が進むごとに、ドリフト項分増えるので、上方トレンドのある系列になります。

$X_t=\alpha +X_{t-1}+u_t$

データを生成する

ドリフト付きランダムウオークを作るには以下の３つが必要です。

• 初期値（ｔ＝0の値）
• ドリフト項の値
• $u_t$系列

初期値は適当な数字を入力すればよいです。オーム社のホームページのダウンロードファイルでは$X_t$の初期値を10、$Y_t$の初期値を20としています。ドリフト項の値は、両系列とも0.5です。

$u_t$については、平均ゼロ、標準偏差１の正規分布をする系列とします。まず、エクセルのRAND()関数で、乱数を発生させます。乱数とは、０から１の間の数値を等確率で不規則に発生させるものです。あくまでも例ですが、以下のような系列です。

0.44、0.80、0.90、0.75、0.34…

これを正規分布をする系列に変換するために、NORM.INV(確率、平均、標準偏差)関数を使います。確率のところに、上のRAND()関数を入れ、平均は０、標準偏差は１とします。以下の関数です。

=NORM.INV(RAND(),0,1)

これをエクセルシートの$u_t$のすべてのセルに入れると、$u_t$ができます。

グラフに描くと以下の系列（ランダムに変化するので同じ系列にはなりません）です。

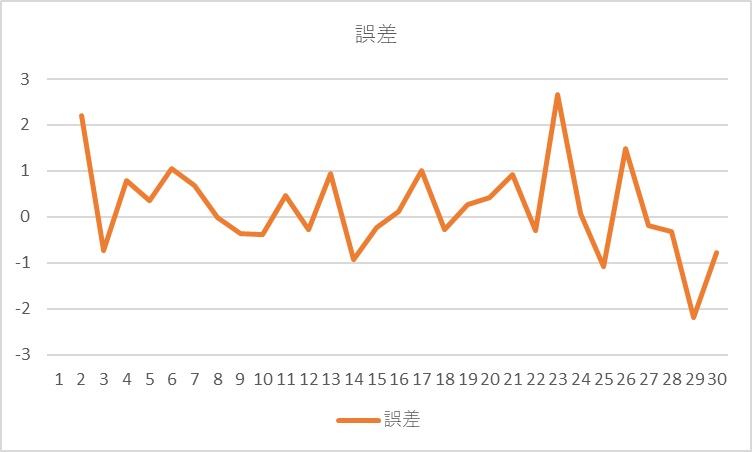
$u_t$ができたので、これを使ってドリフト付きランダムウォークを計算します。ドリフト項は、0.5とした場合は以下になります。

$X_t=0.5+X_{t-1}+u_t$

エクセルでは以下の式をセルに入力することで計算できます。

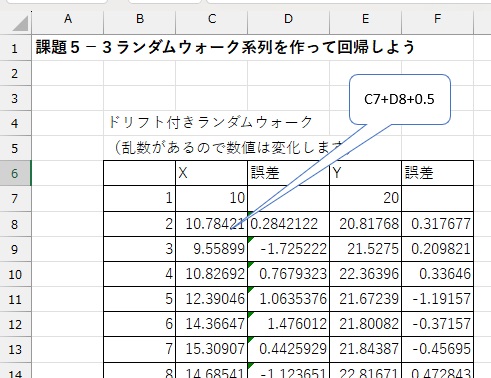
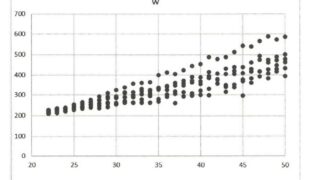
$X_t$と$Y_t$の系列は以下のようになります。

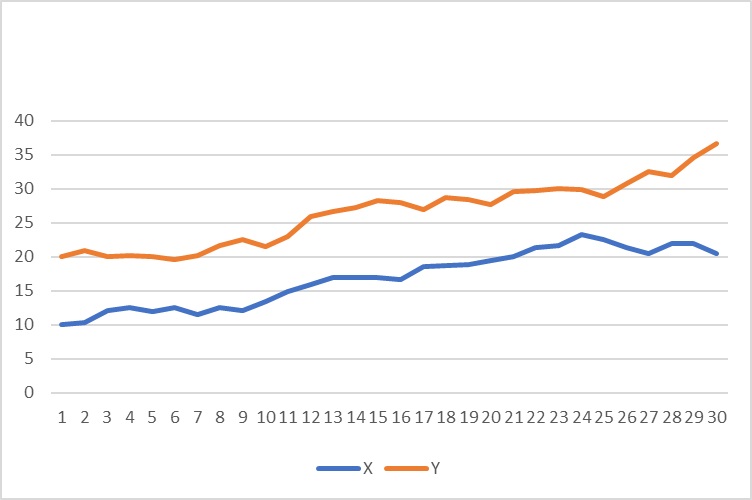
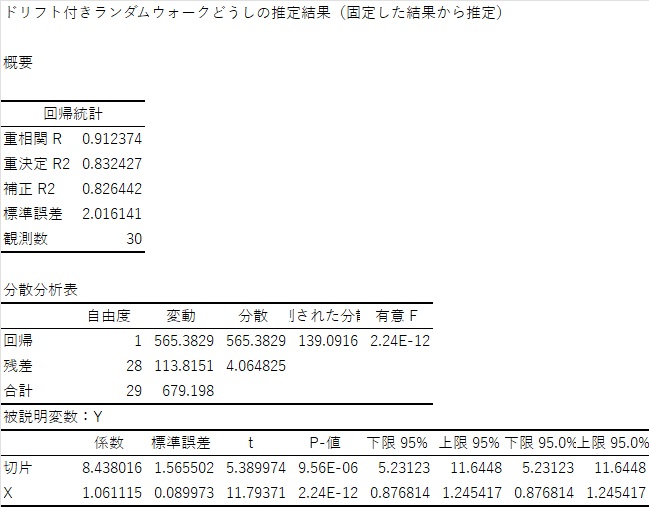
回帰分析

上の系列について、以下の式を推定します。

$Y_t=\alpha +\beta X_t+u_t$

エクセルの推定結果は以下のようになります。人工的に作成した系列ですが、ｔ値は高く、決定係数も高いことが分かります。

• 【python】 クラスとインスタンス
• 【python】関数の作成
• AI関連の分析ツールの紹介ーー生成AIなど
• 【Python】Pythonの基本操作
• 経済学Q＆A（試験編）

検索

検索