確率分布として代表的なものは正規分布ですが、ほかにも二項分布やポアソン分布があります。ポアソン分布については、「不吉な分布」というイメージを持っているんですが、「稀にしか起こらない」ということが関係しているようです。
正規分布に関するエクセルの確率分布関数はこちらをご覧ください。
経済統計の使い方では、統計データの入手法から分析法まで解説しています。


確率分布の種類
確率変数とは、通常の変数と同じように様々な値をとるものですが、値と確率が対応しているところが違います。通常の変数ですと、変数Xには1や2などの数値が入るわけですが、確率変数Xには1や2など数値が入るうえ、1は10%、2は30%など確率が対応しています。
サイコロの場合だと、確率変数は1から6までの値をとり、それぞれの確率は1/6ということになります。
確率変数と確率の対応を現したものが確率分布となります。グラフで描くと、横軸が確率変数、縦軸が確率になります。
| 特徴 | 確率変数の例 | パラメーター | |
| 一様分布 | 同じ確率 | サイコロを振った時の目 | |
| ベルヌーイ分布 | 2つの結果しか生じない 違う確率の場合も | コインの表裏、動物の雌雄 | 成功確率p |
| 二項分布 | ベルヌーイ試行を複数回行った時の成功回数 | コインを10回投げた時の表の回数 | 試行回数N 成功確率p |
| ポアソン分布 | 試行回数が多く、成功確率が少ないケース | 交通事故の死者数 草原での動物の発見個数 不動産の販売個数 | 平均値λ=Np |
| 正規分布 | 平均値に対して左右対称 | 身長 体重 テストの点数 | 平均と分散 |
ベルヌーイ分布
ベルヌーイ分布は、確率変数が2つだけの場合で、コインの表と裏、試合の勝ち負け(引き分けがない場合)、成功と失敗などが例になります。
どちらか一方がとる確率のことを成功確率pと呼びます。ベルヌーイ分布ではコインの表と裏などが代表的ですが、成功確率が同じである必要はないです。
ヤコブ・ベルヌーイは1654年生まれのスイスの数学者です。
二項分布
コイン投げなどのベルヌーイ試行を複数回行った場合の、表がでる回数が二項分布です。ベルヌーイ分布の確率変数は、表と裏ですが、二項分布の確率変数は表の出る回数です。試行回数Nと成功確率pがパラメーターになります。
ポアソン分布
ポアソン分布は、2項分布の試行回数Nを無限に大きくし、成功確率pを無限に小さくしたときに得られる分布です。試行回数と成功確率を掛け合わせた期待値λがパラメーターになります。
試行回数が多いわりに、成功確率が少ない場合ということで、稀に起こる事象の分布になります。
シメオン・ドニ・ポアソンは1781年生まれのフランスの数学者です。
正規分布
正規分布は、自然界に多い分布で、平均を中心に対称の分布になります。身長や体重、テストの点数の分布などを考えるとわかりやすいでしょう。平均と分散を決めると分布が決まります。
二項分布とポアソン分布の比較
離散確率分布で代表的な二項分布とポアソン分布をグラフを描いて比較しましょう。
| 二項分布 | ポアソン分布 | |
| 10回 | 成功確率が0.2,0.5,0.8 | 平均が2,5,8 |
| 100回 | 成功確率が0.02,0.2,0.5,0.8 | 平均が2,20,50,80 |
二項分布で試行回数が10回の場合です。成功確率が0.5の時は左右対称の分布ですが、0.2、0.8の場合は正規分布とは異なります。
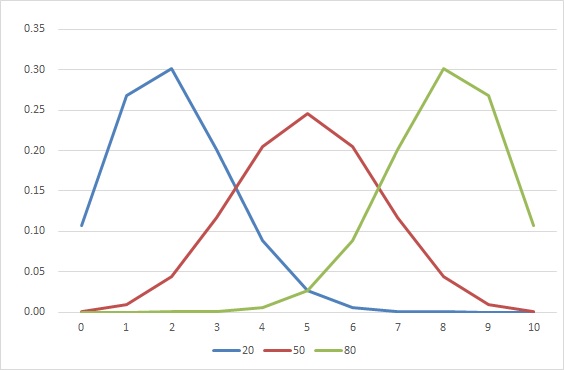
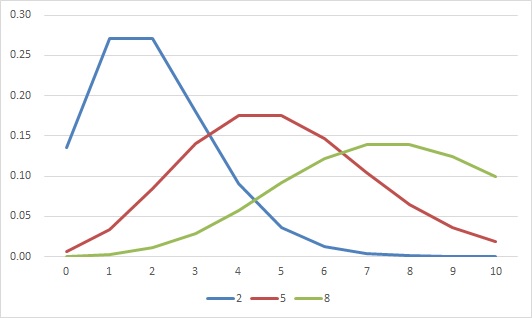
ポアソン分布で試行回数が10回の場合です。平均値が小さい場合は二項分布と似ていますが、平均値が大きくなるにつれ、分散が大きくなります。
二項分布で試行回数が100回の場合です。成功率が0.02の時は、分布の形は違いますが、試行回数が増えていくと正規分布に近くなります。分散は、Np(p-1)で計算でき、pが0.5 の時の標準偏差は5になります。
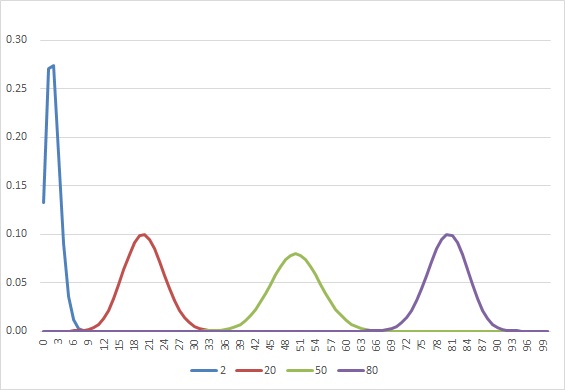
ポアソン分布で試行回数が100回の場合です。特徴的なのは、平均値が大きくなると分散も大きくなるところです。ポアソン分布のパラメーターλは試行回数N×成功確率pで、これが平均値でもあり、分散の大きさにもなります。
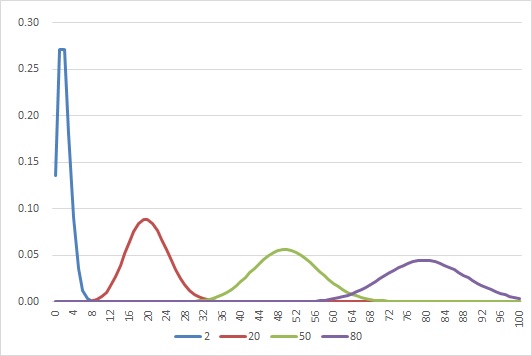
エクセルの関数では
上記のグラフを描いたエクセルの関数を紹介しておきます。
二項分布
$ =BINOM.DIST(確率変数,試行回数,成功率,FALSE) $
ポアソン分布
$ =POISSON.DIST(確率変数,平均値,FALSE) $
- 【時系列分析】課題3 ドリフト付きランダムウォーク
- 【時系列分析】課題2 グレンジャーの因果関係
- 【時系列分析】課題1 為替レートの予測
- 「回帰分析から学ぶ計量経済学」を使ったセミナーを行います(2024年3月8日)
- 正誤表 回帰分析から学ぶ計量経済学