最小二乗法では、t値やF値が出力されます。t値は係数の有意性を調べるもの、F値は式全体に意味があるかどうかを調べるもの、と覚えている人も多いと思います。
ただ、t値やF値は、検定した結果の統計量を表すという一般的な言葉です。t検定やF検定はさまざまな検定に利用されています。この記事では、t検定やF検定といった切り口でさまざまな検定をまとめて見ます。
経済統計の使い方では、統計データの入手法から分析法まで解説しています。

統計的検定とは
統計的な検定とは、棄却すべき帰無仮説をたてて、検定統計量を計算し、帰無仮説を棄却できるかどうかを検定します。有意水準としては1%、3%、5%が使われます。
有意水準とは、「偶然ではおこらないような稀な水準」のことなので、10%だと少し高いですが、10%が使われることもあります。検定は以下の手順で行います。
- 帰無仮説をたてる
- 有意水準を決める(5%など)
- 検定統計量(t値など)を計算する
- 検定統計量の出現する確率(p値)を計算する
- p値が有意水準よりも小さいことを確認
- 帰無仮説を棄却する
p値が有意水準よりも大きければ、稀な水準ではないということで、帰無仮説が受容されることになり、想定していた主張ができないことになります。
t検定
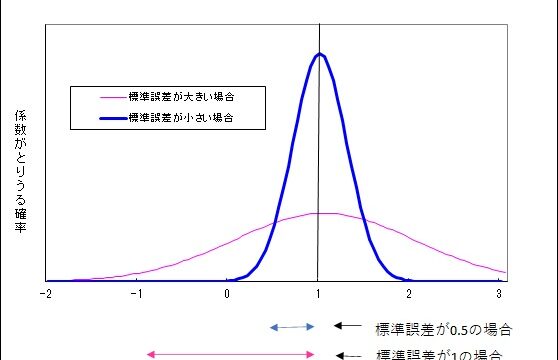
t検定は、統計学では平均値の差の検定に使われます。計量経済学では、これを利用して、係数(平均値)がゼロと有意に異なるかどうかを検定します。

係数の有意性の検定
t検定として最もよく使われるのが、係数が有意かどうかの検定です。係数がゼロであると仮定してt値を計算し、その出現する確率(p値)を計算します。p値が小さければ、「係数がゼロである」ことが棄却され、係数がゼロ以外の値であることが主張できます。
帰無仮説:係数=0である。
最小二乗法で推計すると、係数ごとにt値が計算されます。2以上あれば有意と考えられます。
係数がある値であるかどうかの検定
よく使われるのは、係数=0の検定ですが、係数が1や2であるかどうかの検定もできます。$ Y_i=\alpha+\beta X_i+e_i $で $ \beta=K $の検定をする場合は、以下の検定をすればよいです。
$t=\dfrac{\beta-K}{\beta の標準誤差}$
帰無仮説:係数は$K$である
単位根検定
単位根検定でもt値が使われます。$ \Delta X_t=\rho X_{t-1}+e_t $の$\rho$に関する検定です。ただ、棄却水準は通常のt分布とは異なることに注意が必要です。
帰無仮説:$\rho$ がゼロ
F検定
2つの残差二乗和は、nをサンプル数、pを無制約モデルの定数項を含めた説明変数の数、qを制約の数として、以下のF分布に従います。これを利用して検定をします。
$F= \dfrac{(SSR_r-SSR)/q}{( SSR )/(n-p-q)}$
「係数制約がある」という帰無仮説のもとで、F値を計算し、それが偶然起こるには程遠いほど確率(p値)が低ければ、帰無仮説を棄却し、「係数制約がない」という結論を導き出します。
- 帰無仮説 係数制約がある
- 対立仮説 係数制約がない
- F値が大きい(p値が小さい) 係数制約がない
式に意味があるかどうかの検定
式に意味があるかどうかの検定とは、推計された係数のうち、少なくとも一つはゼロではないということです。帰無仮説は、「すべての係数がゼロ」です。帰無仮説のもとでは、その式に含まれる説明変数は被説明変数に影響を与えないことを示します。
帰無仮説:回帰係数がすべてゼロである
係数制約の検定
係数が制約がある場合と無い場合の検定です。係数に制約がない場合の残差二乗和と、係数に制約があるばあいの残差二乗和を計算し、これに大きな違いがある場合は係数制約に意味があるということになります。「係数が等しい」という帰無仮説のもとでF値を計算し、規約できれば係数の制約に意味があるということになります。
帰無仮説:係数が等しい
構造変化の検定
構造変化の検定は、構造変化前と構造変化後の残差二乗和が変わらないかどうかを調べます。構造変化の前後で、残差二乗和が大きく変わる場合は構造変化があるものとします。
帰無仮説:構造変化前と構造変化後の残差二乗和に変化がない
グレンジャーの因果関係の検定
グレンジャーの因果関係は、過去の変数が有意かどうかを検定するものです。帰無仮説「過去の係数がゼロ」のもとでF値を計算し、棄却できるかどうかを検討します。
帰無仮説:過去の係数がゼロである。
F検定について詳しくは以下の記事をご覧ください。

χ(カイ)二乗検定
ホワイトテスト
ホワイトテストは、不均一分散の検定です。残差の二乗を説明変数や説明変数どうしの積に回帰してその係数を調べます。それらが残差の二乗に影響を与えていたら、不均一分散があると判断します。帰無仮説は「残差の二乗推計の係数がすべてゼロである」で、検定統計量を計算します。p値が小さければ、帰無仮説が棄却され、不均一分散が疑われます。
帰無仮説:残差の二乗推計の係数がすべてゼロである
J検定
GMM(一般化モーメント法)で、推定がうまくいっているかどうかの検定です。
一般化モーメント法はモーメント条件を使って推定する手法です。「操作変数と誤差項に相関がない」という条件を使う場合がありますが、操作変数が説明変数よりも多い場合は過剰識別となります。それでもうまく推定できているかどうかをJ検定によって検定します。
帰無仮説:モーメント条件はゼロと等しい。
この場合のモーメント条件とは「操作変数と誤差項の相関がゼロ」なので、この帰無仮説にそって検定統計量を計算します。この場合は、帰無仮説が棄却されれば、推定がうまくいっていないということなります。推定がうまくいっていることを主張するには帰無仮説が受容されないといけません。
ハウスマン検定
ハウスマン検定は、パネルデータで、固定効果と変量効果を選択する場合の検定です。帰無仮説は、「ランダム効果と説明変数に相関がない」で、これを前提に検定統計量を計算します。ランダム効果と誤差項に相関がない場合は、変量効果モデルで推定した方が望ましいです。
帰無仮説:ランダム効果は説明変数と相関がない
これを前提に検定統計量を計算して、p値が小さければ帰無仮説が棄却され、固定効果モデルを選択します。
まとめ
- この記事ではさまざまな検定についてまとめました
- t検定は係数が有意かどうかなどの検定です
- F検定は係数制約などの検定です
- χ(カイ)二乗検定は不均一分散などの検定です
- 【時系列分析】課題3 ドリフト付きランダムウォーク
- 【時系列分析】課題2 グレンジャーの因果関係
- 【時系列分析】課題1 為替レートの予測
- 「回帰分析から学ぶ計量経済学」を使ったセミナーを行います(2024年3月8日)
- 正誤表 回帰分析から学ぶ計量経済学