回帰分析をすると、係数は簡単に計算できます。問題はその数字をどのように解釈するかということです。検討するポイントベスト3をまとめておきました。
回帰分析は被説明変数を$y_i$説明変数を$x_{1i}$、$x_{2i}$とした時、以下の式の係数$\alpha$、$\beta_1$、$\beta_2$を求めることです。
$ y_i=\alpha + \beta_1 x_{1i} +\beta_2 x_{2i} +e_i $
経済統計の使い方では、経済統計の入手法から分析法まで解説しています。

第1位 符号条件
推定しようとする式には、理論的なモデルが背景に必要です。そのモデルから期待される符号条件と合っていないと統計的には正しくても、使えない式になります。
たとえば、所得が消費によって決まると考える場合、期待される符号条件はプラスです。これがマイナスになってしまうと、理論モデルを否定することになってしまいます。
第2位 t値
t値は、$\beta_1$や$\beta_2$が統計的に有意かどうかを調べるものです。帰無仮説は$\beta_1$に関しては、「$\beta_1$はゼロ」なので、t値が低いということは、$\beta_1$はゼロである($x_{1i}$が$y_i$に影響を与えない)ことが否定できないということになります。
棄却域の設定にもよりますが、t値が2以上あれば、その係数は有意に被説明変数に影響を与えていると考えられます。
F値の帰無仮説は、「$\beta_1=\beta_2=0$」です。帰無仮説が棄却されるということは、$\beta_1$か$\beta_2$の少なくとも一つはゼロではない、ということです。式全体として、意味があるかどうかを判断する場合に使います。
第3位 決定係数
決定係数は、当てはまりを表す指標で、0から1までの値をとり、高ければ高いほど、当てはまりが良いことを示します。0だと説明変数が被説明変数を全く説明しておらず、1であればすべて説明していることを表します。
決定係数は、通常の決定係数と自由度修正済み決定係数が出力されますが、自由度修正済み決定係数だけみていれば大丈夫です。決定係数はサンプル数が少ない場合や説明変数が多い場合に高めにでるので、それを修正したものです。修正後の方が低めになるので、こちらで判断する方が慎重な判断と言えます。
予測に使う場合では、決定係数は高ければ高いほどよく、0.9以上の高さは欲しいところです。
分析に使う場合は決定係数が特に高い必要はなく、むしろ変数のt値に注目する場合が多いです。t値が高ければ、その説明変数が被説明変数に影響与えることが主張できるためです。ただ、決定係数が低い場合は、必要な説明変数が式に入ってない場合が多いので、決定係数を高める努力は必要でしょう。
ダービン・ワトソン比も
時系列データでは、ダービン・ワトソン比も調べておいた方が良いでしょう。残差に自己相関があるかどうかを調べることができます。残差に自己相関がある場合は、必要な説明変数が入っていない場合が多いです。
具体例
実際の為替レートを購買力平価で回帰した場合の例です。被説明変数が実際の為替レート、説明変数がGDPデフレーターで測った購買力平価(世界銀行のデータ)です。
$ 為替レート=78.8+0.23×購買力平価(GDPデフレーター)$
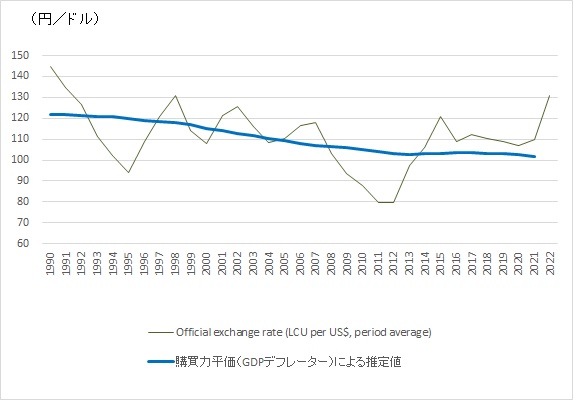
エクセルを使って推計しました。推定期間は1990年から2021年です。
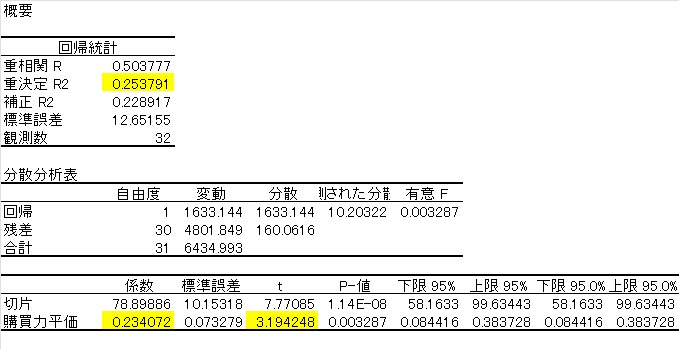
まず、符号条件を見ます。係数は0.23なので、プラスです。購買力平価と為替レートが同じ方向に動くということです。t値は3.19なので2以上あり、購買力平価が為替レートに影響を与えていることがわかります。自由度修正済み決定係数(重決定R2)は0.25で1には程遠いです。グラフをみても、ほぼ当てはまっていないことがわかります。
それでも、購買力平価からみた為替レートの水準を計算することができ、有用な情報を提供してくれます。