最小二乗法はさまざまな仮定のもとに最も優れた推定値（BLUE)になります。
最小二乗法の仮定が満たされない場合とその問題点、解決法を解説します。
経済統計の使い方では、統計データの入手法から分析法まで解説しています。
わかりやすくまとめました。
| 仮定 | 満たされない場合 | 問題 | 解決法 |
| 線形関数 | 双曲線、対数関数など | 変数を加工しなければ推計できない。 | 説明変数を変形する |
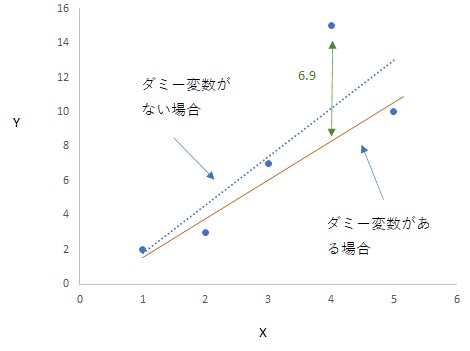
| 残差の平均はゼロ | 定数項がない場合 | 決定係数が使えない | 特に問題はない |
| 残差の分散は均一 | 不均一分散 | 係数に不偏性はあるが効率性がない | ホワイト、一般化最小二乗法 |
| 〃 | 誤差項の自己相関 | 〃 | コクラン・オーカット法など |
| 説明変数は誤差と無相関 | 説明変数の内生性 | 係数に不偏性も有効性もない | 操作変数法、2段階最小二乗法 |
| 説明変数に相関がない | 多重共線性 | 係数の分散が大きい | 変数を減らしたり、加工したりする。 |
線形関数
線形関数でなくても、説明変数を加工することで、推計できる場合があります。詳しくはこちらをご覧ください。
残差の平均はゼロ
残差の平均をゼロにするには、定数項があれば事足ります。残差の平均がゼロでないのは定数項がない場合の推計です。ｔ値などは問題ないですが、決定係数に関しては注意が必要です。
通常の決定係数は以下の式で計算されます。
$決定係数＝\dfrac{ \Sigma(\hat{Y_i}-\bar{Y} )^2}{\Sigma(Y_i-\bar{Y} )^2}$
残差の平均がゼロでないと、推定値の平均と本来の値の平均とにずれが生じます。残差の平均がゼロでない場合の決定係数は、次の方法で計算することが適当です。分子の部分が、$Y$の平均から推定値$\hat{Y}$の平均へと変わっています。
$決定係数＝\dfrac{ \Sigma(\hat{Y_i}-\bar{\hat{Y}} )^2}{\Sigma(Y_i-\bar{Y} )^2}$
しかし、統計ソフトによっては最初の式で計算する場合もあり、注意が必要です。
さまざまな決定係数の計算法があることについては、以下の記事の最後のあたりをご覧ください。
不均一分散
残差が均一でない場合は、不偏性はありますが、効率性はありません。通常の最小二乗法で計算すると、t値が本来よりも小さ目に計算されて、有意なものを有意でないとする場合があります。誤差項に系列相関がある場合も不均一分散の一種です。
不均一分散があっても、不偏推定量ではあるので、係数はそのまま使えます。標準誤差に関してはホワイトの推定量などを使います。
誤差項の系列相関の場合は、コクランオーカット法などにより、処理します。
説明変数の内生性
説明変数が誤差と相関していないというのが仮定ですが、それが満たされない場合です。具体的には以下のケースです。
- 需要曲線と供給曲線の推定
- 同時方程式モデル
- 計測誤差がある場合
- 欠測値がある場合
操作変数法を使うことで対処できます。
さらに詳しくは、以下の記事をご覧ください。
説明変数が相関
説明変数が相関している場合は多重共線性があると呼ばれます。
最小二乗法の統計的な特性として何か問題があるわけではないですが、係数の分散が大きくなることが問題です。サンプルが少し増えただけで大きく係数が変わる可能性があります。
対処法としては、説明変数の選び方を工夫する必要があります。
まとめ
- この記事では、最小二乗法がBLUEであるための仮定とそれが満たされない場合の対処方にについて解説しました。特に以下の２つが重要です。
- 不均一分散の場合は、有効性がなくなる。対処法としては、一般化最小二乗法など。
- 説明変数に内生性がある場合は、不偏性も有効性もみたされない。対処法としては、操作変数法など。
- 【時系列分析】課題３ ドリフト付きランダムウォーク
- 【時系列分析】課題２ グレンジャーの因果関係
- 【時系列分析】課題１ 為替レートの予測
- 「回帰分析から学ぶ計量経済学」を使ったセミナーを行います(2024年３月８日）
- 正誤表 回帰分析から学ぶ計量経済学
