ダミー変数とは擬似変数とも呼ばれ、1とゼロからなる変数です。
大きく分けると
- 1時点の異常値を処理する異常値ダミー
- 定数項を調整する定数項ダミー
- 係数を調整する係数ダミー
があります。
経済統計の使い方では、統計データの入手法から分析法まで解説しています。

異常値ダミー
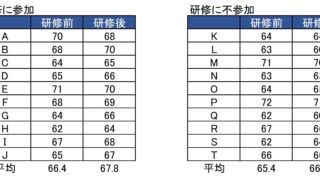
最小二乗法は、異常値に弱い推計法でもあります。たとえば、以下のデータを仮想例として使ってみましょう。
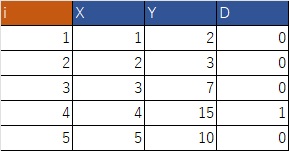
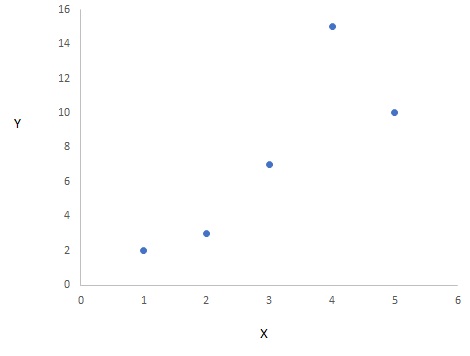
$X_i$と$Y_i$はだいたい相関していますが、第4期のx=4、Y=15のデータは異常値になっています。散布図で描くとよくわかります。
異常値は、戦争やストライキ、天候不順、政策変更などが原因で発生します。
このまま最小二乗法を適用すると以下の式になります。自由度修正済み決定係数は0.59です。
$ Y_i=-1.0+2.8X_i$
第4期の$Y_i$の値が異常値と考え、第4期であるX=4の時1,それ以外は0のダミー変数$D_i$を説明変数に加えます。そうすると、本来の係数が推定できます。
$X_i$にかかる係数が2.8から2.1へと減少し、決定係数は0.97に上がりました。ダミー変数にかかる係数は6.9なので、第4期は理論値より6.9だけ上に上がったことがわかります。
$ Y_i=-0.3+2.1X_i+6.9D_i$
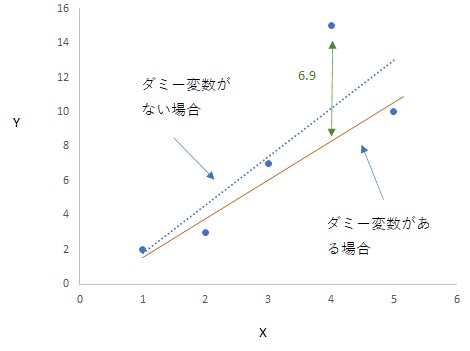
このように、ダミー変数を利用することにより、適切な推定が行われます。
定数項ダミー
最小二乗法の定数項や係数にもダミー変数を使うことができます。まず、定数項ダミーです。
二つのカテゴリーがあって、傾きは同じだけれど水準が違う場合に使えるものです。ここでは、男女の身長を並べたデータを使ってみましょう。1年間の身長の伸びは同じと考え、男女の身長差をダミー変数で測るとします。
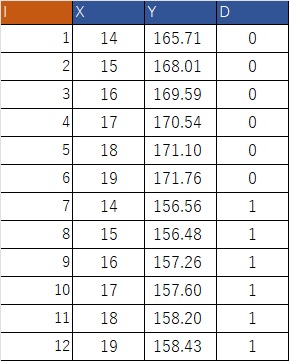
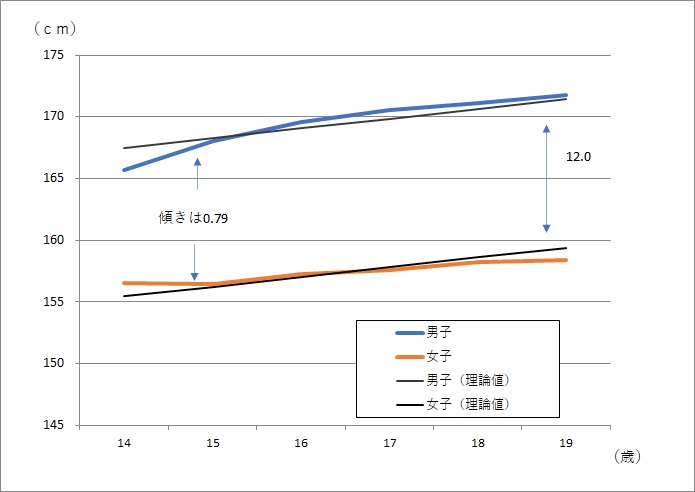
$X_i$は年齢、$Y_i$は身長です。$D_i$はダミー変数で男子の場合は0、女子の場合は1にしています。最小二乗法で係数を推定すると以下の式となります。
$Y=156.4+0.79 X-12.0D $
男女とも年間0.79cm身長が伸び、男女の差は12.0cmあることがわかります。
係数ダミー
係数ダミーは、カテゴリーによって傾きが変わる場合です。サラリーマンの昇給ペースは、一般職と総合職、正規職員と非正規職員など職種によって違います。こうした例では係数ダミーを使って両者を統合して分析することができます。以下の仮想的なデータを使います。
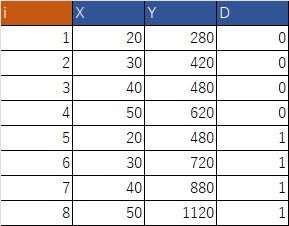
散布図で表すと以下のデータです。
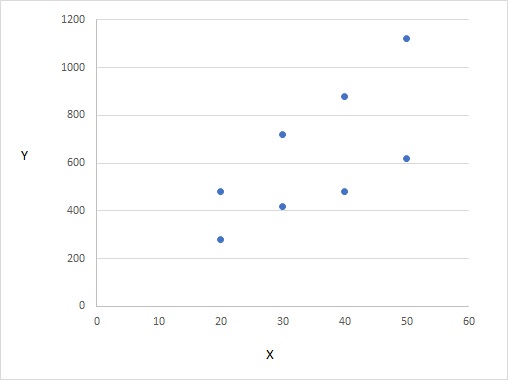
$X_i$は年齢、$Y_i$は年収を表しているとします。ダミー変数$D_i$は一般職は0、総合職は1とします。両方とも、年齢とともに収入が増えますが、増え方が違うモデルで、以下の式になります。
$Y_i=\alpha+\beta_1 X_i+\beta_2 D_i X_i+e_i$
ダミー変数が0の時、傾きは$\beta_1$、ダミー変数が1の時傾きは$\beta_1+\beta_2$ということです。
実際の推計結果は以下になります。一般職は年間10万円収入が増え、総合職では年間20万円収入が増えるという結果になっています。
$Y_i=72.0+10.8X_i+10.0 D_i*X_i $
仮説検定に利用できる
ダミー変数を用いた推定は、さまざまな仮説検定に利用できます。
たとえば、定数項ダミーのケースでは、
男女の身長に差があるかどうか
の検定ができ、係数ダミーのケースでは、
一般職と総合職の昇給ペースに違いはあるか
という検定ができます。ダミー変数の係数のt値を調べればよいです。
t値は、「係数がゼロ」の対する仮説検定なので、t値が有意だということは、「ダミー変数の係数がゼロ」という帰無仮説を棄却できることを表します。「男女の身長に差がある」という帰無仮説を棄却でき、男女の身長に差があると結論づけられます。
被説明変数の場合は質的従属変数に
被説明変数に1,0の変数を使う場合があります。就職している=1、就職していない=0といった変数を使う場合です。この場合は、質的従属変数と呼び、特有の推定法が考案されています。
EViewsで異常値ダミーを使う
EViewsで、一時点ダミーを使って例を説明します。使うのは、農林水産省の「作物統計」です。2000年から水稲の作付面積と収穫量を使いました。
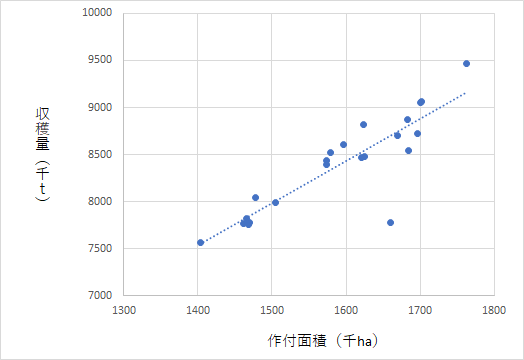
近似曲線を引くと、一つだけ大きく外れた点があります。2003年で、記録的な冷夏だったため、作付面積に比べて、収穫量が大きく落ち込んでいます。
作付面積から収穫量を予測する場合、2003年の異常値に引きずられる可能性があるため、ダミー変数を使って処理することにします。

- 【時系列分析】課題3 ドリフト付きランダムウォーク
- 【時系列分析】課題2 グレンジャーの因果関係
- 【時系列分析】課題1 為替レートの予測
- 「回帰分析から学ぶ計量経済学」を使ったセミナーを行います(2024年3月8日)
- 正誤表 回帰分析から学ぶ計量経済学