多重共線性とは、説明変数どうしの相関が高いと起こる現象で、相関している変数それぞれの係数の標準誤差が大きくなる現象です。
サンプルを変えただけで係数が大きく動き、正負の符号が反対になる場合もあります。
多重共線性があるかどうかの検定にはVIF（Variance Inflation Factor)を使います。10以上であると多重共線性があると判断されます。
多重共線性がある場合は、相関している変数のいずれかを除くのがよいですが、両方使いたい場合は平均をとったり、主成分分析を使って、相関の無い変数に変化する方法があります。
経済統計の使い方では、統計データの入手法から分析法まで解説しています。
多重共線性＝説明変数どうしの相関が高いこと
最小二乗法が優れた結果をもたらす条件として、「説明変数に相関がない」があります。
多重共線性（multicollinearity）は、説明変数どうしに相関がある場合のことです。
英語の略で「マルチコがある」などと呼ばれることもあります。相関が高い場合は通常線形の関係にあるので、共線性と呼びます。
標準誤差が大きくなる
多重共線性がある場合、係数の標準誤差が大きくなります。係数が最小二乗法によって推定できたとしても、確率的に存在する範囲が広いということです。その結果以下のような症状が出てきます。
- サンプルを少し変えただけで結果が大きく変わる
- 標準誤差が大きいのでｔ値は小さくなる
- 想定された符号と反対になる場合もしばしばある
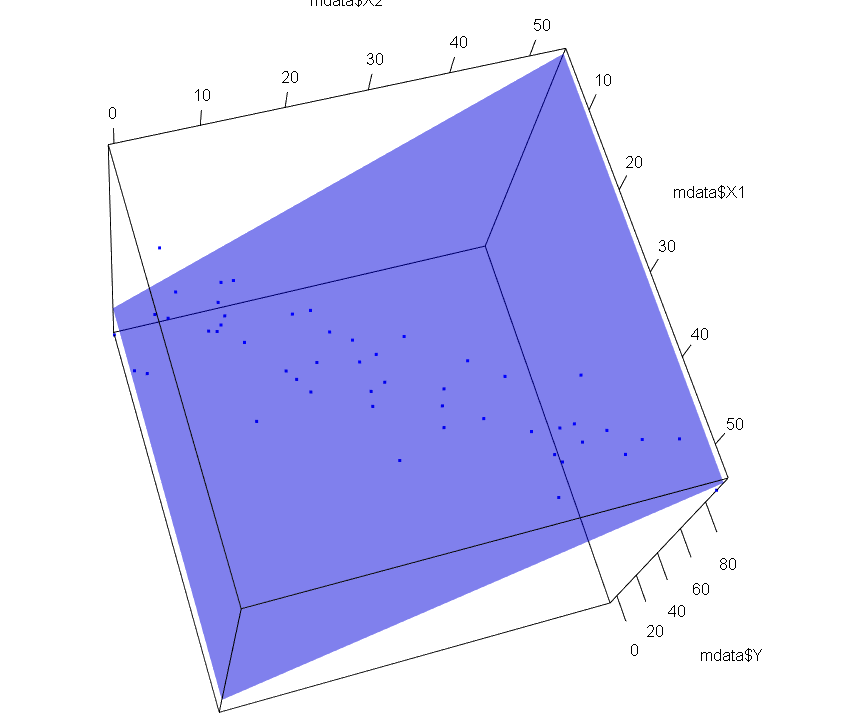
3Dグラフでみると
３Dグラフでみると、説明変数がX1とX2が相関していない場合、Yを推計した平面はどっしり落ち着いています。多少サンプルが増えても減っても係数が揺らがないです。
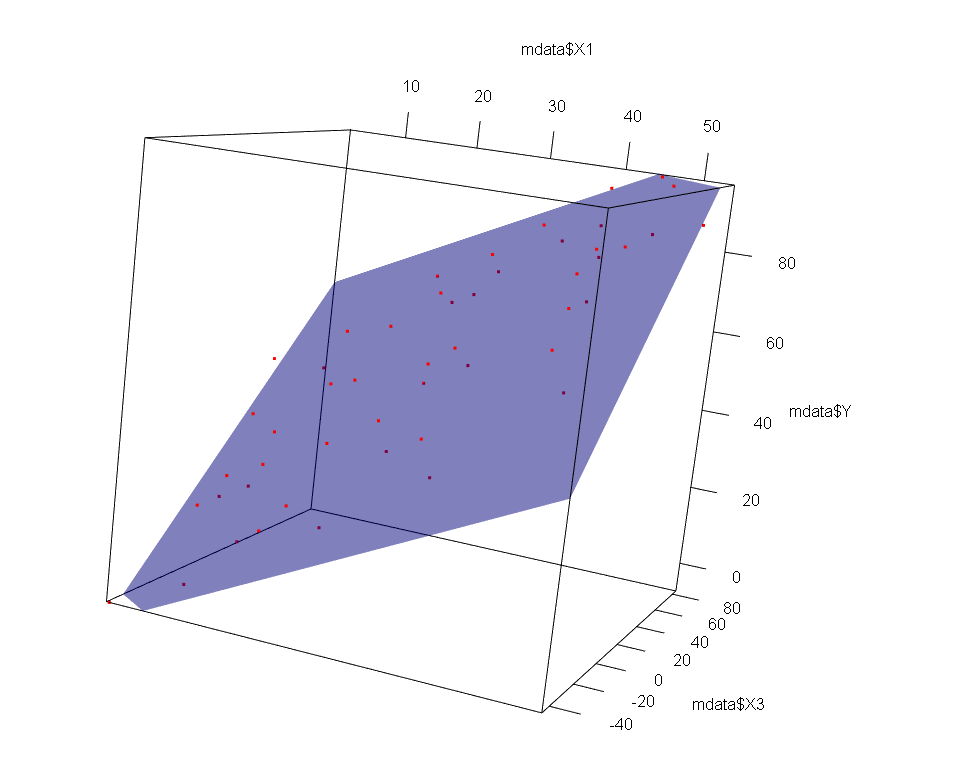
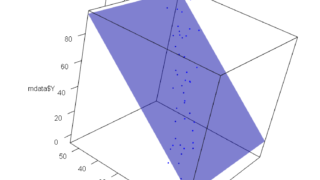
下のグラフは、説明変数X1とX2が相関している場合です。Yに回帰した平面は定まらず、サンプル数が少し増えただけで大きく平面の傾きが変わりそうです。
多少わかりにくいと思いますので、動画もみて下さい。点が平面を支えていない様子がわかると思います。
３Dグラフの描き方は最後を参考にしてください。
発見にはVIF
多重共線性があるかどうかを発見するには、VIF（Variance Inflation Factor）を使います。分散膨張要因という意味ですが、係数の誤差を広げる要因ということです。
変数同士に相関があるかどうかを見つけるという意味では相関係数でよいのではないかという気もします。確かに、２変数であれば相関係数を見ても多重共線性があるかどうかはわかります。しかし、３変数以上になると、それぞれの組み合わせを計算する必要があります。場合によっては、ある変数とほかの変数２つの組み合わせで相関が高い可能性もあります。そこで、３変数$X_1$、$X_2$、$X_3$の場合、たとえば$X_1$に$X_2$、$X_3$を回帰して、その決定係数を調べます。
$ X_1=\alpha+ \beta_1 X_2 + \beta_2 X_3 $
VIFはその決定係数$R^2$を加工したもので、以下の式になります。
$ VIF= \dfrac{1}{1-R^2} $
決定係数が高いということは、$X_1$が$X_2$と$X_3$に相関しているということを表し、VIFは大きくなります。
多重共線性の目安として、VIFが10以上だと多重共線性が疑われるといわれています。
2変数の場合で相関係数とVIFの関係をみるとVIFが10ということは以下の式が成り立つとういことです。
$ 10= \dfrac{1}{1-R^2} $
決定係数が0.9、相関係数に直すと平方根をとって0.95ということになります。
多重共線性への対処
多重共線性は相関の高い変数が入っているということなので、VIFが最も高い変数を外すことが有効です。その変数を除いても、ほかに相関が高い変数が入っているので、推定結果は大きな影響を受けないはずです。
相関の高い変数がわかっていて、しかも両方の変数を入れたい場合は、平均をとって新たな説明変数とすることが考えられます。
別の方法として、相関の高い変数群を主成分分析にかけて、第1主成分、第2主成分などを説明変数とすることが考えられます。主成分どうしは相関がないので、多重共線性の問題は生じません。
具体例
以下の仮想データを使って多重共線性の影響を見ていきましょう。使ったデータはここにあります。サンプル数は50です。
- $X_１$と$X_２$には高い相関関係
- $X_３$は$X_１$と$X_２$と低い相関関係
- $Y$は $ Y＝１＋0.5X_１＋0.5 X_２＋0.5X_３＋e $で計算する。
推定結果
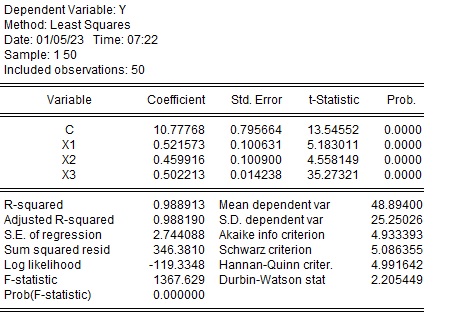
推定結果は以下の結果になりました。
$ Y＝\alpha ＋\beta_1 X_１＋ \beta_2 X_２＋ \beta_3 X_３＋e $の結果です。
$\beta_1$と$\beta_2$の標準偏差が$\beta_3$に比べて大きいことがわかります。また、係数が真の値の0.5から外れており、$\beta_1$は0.52、$\beta_2$は0.46です。一方、$\beta_3$は真の値の0.50が推定されています。
| 変数 | 係数 | 標準誤差 | t値 |
| $\alpha$ | 10.78 | 0.80 | 13.5 |
| $\beta_1$ | 0.52 | 0.10 | 5.2 |
| $\beta_2$ | 0.46 | 0.10 | 4.6 |
| $\beta_3$ | 0.50 | 0.014 | 35.3 |
サンプル数を変えた場合
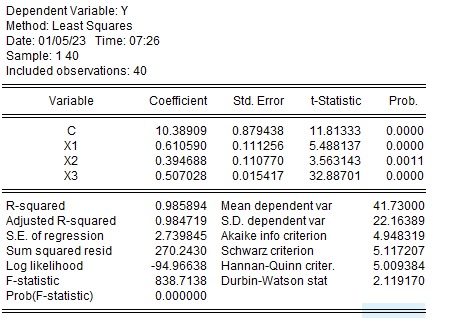
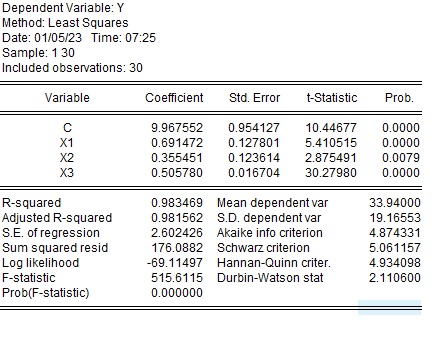
サンプルを1～40、1～30に変えた場合の$X_1$、$X_2$の係数は以下のように大きく変わります。一方で、$X_3$は0.5で変化がありません。
| サンプル数 | 1－50 | 1－40 | 1－30 |
| $\alpha$ | 10.78 | 10.39 | 9.97 |
| $\beta_1$ | 0.52 | 0.61 | 0.69 |
| $\beta_2$ | 0.46 | 0.39 | 0.36 |
| $\beta_3$ | 0.50 | 0.51 | 0.51 |
VIFの計算
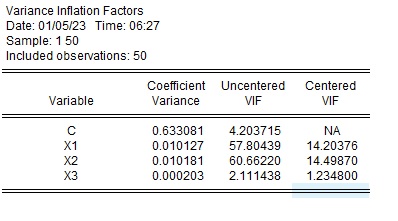
VIFを計算すると、各変数は以下の結果になりました。
- $X_1$ 14.2
- $X_2$ 14.2
- $X_3$ 1.2
$X_1$と$X_2$は10を超えているので多重共線性が疑われますが、$X_3$は1.2で多重共線性の心配はなさそうです。
$X_2$を除いた推定
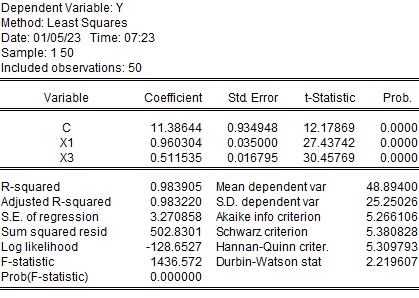
多重共線性が疑われるX2を除いて推定すると以下の結果となります。$X_1$の係数は$X_1$と$X_2$を合わせた係数となっていて、標準誤差が小さくなっています。
| 変数 | 係数 | 標準誤差 | t値 |
| $\alpha$ | 11.4 | 0.93 | 12.2 |
| $\beta_1$ | 0.96 | 0.035 | 27.4 |
| $\beta_3$ | 0.51 | 0.017 | 30.5 |
EViewsの出力例
詳しいデータが見られるようにするため、EViewsの推定結果も載せておきます。
基本的な推計
サンプル数40の場合
サンプル数30の場合
VIFの結果
$X_2$を除いた推定
３DグラフのRプログラム
library(rgl)
Y <- c(-7.382379268,10.04525675,11.43096839,-2.812232976,38.9330499,4.644860325,37.95110956,30.30746641,21.27520163,27.88925466,16.53575991,40.74465021,15.5376137,48.02570672,38.51752886,51.98384109,11.98476026,13.76414091,18.38622325,30.27168343,64.05342122,59.22072479,61.44983601,36.11994684,67.68128579,44.77814685,31.05747307,49.25653848,62.18772392,54.38183721,71.79613648,37.70836203,29.32894718,77.46744851,82.79381373,50.33937402,80.98123632,78.73075469,73.62877477,67.897976,76.59519218,51.08151006,91.43375427,58.89134899,83.52355582,66.96390632,94.82950387,96.55055589,81.85841498,88.26169446)
X1 <- c(2.440188768,4.450849014,5.629768867,8.793044504,2.0706635,10.9611757,7.881501783,6.406220668,10.79006802,10.30987915,6.095221446,16.66030781,9.360227339,10.18875588,13.41652702,16.74947306,16.2894293,22.10108461,18.80799965,19.37111184,19.1402202,22.88767096,21.70260041,23.8411326,27.10879985,26.97347737,26.61440853,27.03063463,25.73741696,30.3637381,26.15907211,32.36210448,33.73917947,34.35108284,39.18631761,31.66614607,32.18503124,41.30349935,40.9818104,42.9754795,41.3596405,45.72965915,38.46156947,42.83157635,46.97401773,42.26308488,47.34501729,45.67811674,46.61572207,53.80333624)
X2 <-c(-0.649703042,4.493575454,5.983626582,0.461643678,5.627072867,1.627813163,6.091999065,12.66643753,11.05267876,12.08547826,12.66915342,12.45544232,10.42762015,12.74102875,10.41128824,18.22320224,19.20548891,13.29104572,19.60461483,21.64448102,19.23488657,23.60684303,20.9627053,19.1454012,22.62386547,25.57150781,26.81270623,27.04142292,25.49155051,33.21011217,28.17270435,33.94906067,28.21355524,37.37001122,32.52217023,32.89338169,33.17757392,37.9961197,42.21963883,41.50432474,43.53122471,43.01734653,43.56971181,43.63719754,46.8202558,45.42813934,47.10403215,43.28874187,53.88970072,54.57135611)
X3 <- c(-45.80872048,-8.952935398,-1.290361542,-32.9463509,44.67597214,-13.32017372,50.94585171,11.85265613,-0.561481231,7.558929224,0.056794708,26.20078517,-1.482391723,53.31512712,27.00599607,48.90952857,-27.02091851,-18.87992427,-24.22718792,-4.393970993,68.05196374,59.12177835,56.37379808,5.06963622,68.87348076,17.0229676,-3.422655184,18.47155988,58.55552171,16.78902121,68.06196792,-14.26081439,-13.42009307,73.0689982,72.11210165,20.3252936,69.81355273,53.04143587,39.29810837,35.90801218,55.84833646,2.791433035,84.24168066,10.43529196,60.9668567,25.33556029,74.39033474,75.36707129,36.62491456,52.10444109)
mdata <- data.frame(cbind(Y,X1,X2,X3))
plot3d(mdata$X1,mdata$X2,mdata$Y,type="p",col="blue")
fit <- lm(Y ~ X1+X2 , mdata)
coefs <- coef(fit)
planes3d(coefs, coefs, -1, coefs, col="blue", alpha=0.5)
library(rgl)
plot3d(mdata$X1,mdata$X2,mdata$Y,type="p",col="blue")
fit <- lm(Y ~ X1+X2 , mdata)
coefs <- coef(fit)
planes3d(coefs[2], coefs[3], -1, coefs[1], col="blue", alpha=0.5)次にもう一つグラフを描きます。
plot3d(mdata$X1,mdata$X3,mdata$Y,type="p",col="red")
fit <- lm(Y ~ X1+X3 , mdata)
coefs <- coef(fit)
planes3d(coefs[2], coefs[3], -1, coefs[1], col="blue", alpha=0.5)
そのほかにもいろいろと問題がある
