GDPを生産関数の形で推定してみましょう。労働と資本を生産要素として、コブ・ダグラス型生産関数で推定してみてください。
経済統計の使い方では、経済統計の入手法から分析法まで解説しています。

コブ・ダグラス型生産関数
GDPの生産関数を推計してみましょう。コブダグラス型の生産関数は以下の式で表されます。Yは実質GDP、Aは全要素生産性、Kは資本ストック、Lは労働投入量を表します。
$ Y=AK^αL^{1-α} $
両辺を対数にすることで、最小二乗法でも推計できるようになります。
$ log(Y)=αlog(K)+(1-α)log(L)+log(A) $
αについてまとめます。
$ log(Y)-log(L)=α(log(K)-log(L) )+log(A)$
Log(A)の部分は全要素生産性と呼ばれますが、この中には時間ともに進歩する技術進歩の部分があるので、定数項に加え、トレンド変数(T=1,2,…,i)も説明変数とします。
最小二乗法で推定するのは以下の式です。
$ Z_i=a+bX_i+cT_i $
ただし
$ Z_i=log(Y)-log(L) $
$ X_i=log(K)-log(L) $
データ
Yは実質GDPです。資本ストックKは、内閣府の「固定資本ストック速報」の2022年10-12月期速報値の民間資本ストックを使いました。
Lは就業者数に労働力時間をかけたものとして計算しました。就業者数は総務省の「労働力調査」を使います。
e-Statでは、労働力調査→データベース→年度次→1-1-2農林業・非農林業、従業上の地位別就業者数(1953年度~)
労働力時間は厚生労働省「毎月勤労統計」の総労働時間(5人以上)を使います。
e-Statでは、毎月勤労統計調査 全国調査→長期時系列表 →月次・年次・年度次・半期・四半期→29 総労働時間 指数及び増減率ー就業形態計(5人以上)
課題としてのデータは以下を使ってください。
データの推定結果は以下の通りです。
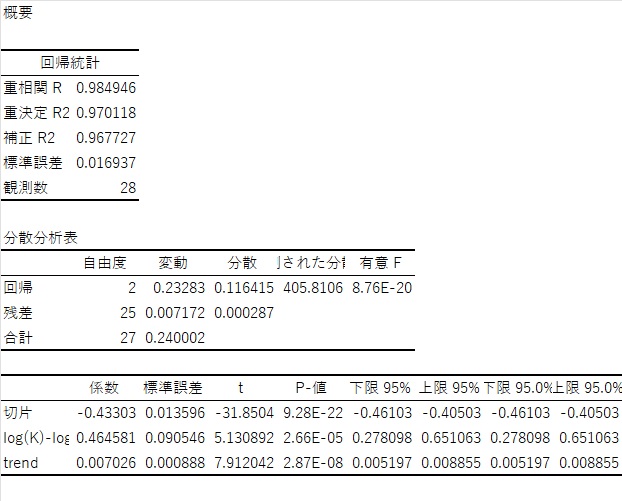
この結果を式に表すと以下になります。
$ log(Y)=0.46log(K)+0.54log(L)-0.43+0.007T $
コブ・ダグラス型生産関数の性質から、労働分配率が54%、資本の労働分配率が46%で、技術進歩率は0.7%ということがわかります。
- 【時系列分析】課題3 ドリフト付きランダムウォーク
- 【時系列分析】課題2 グレンジャーの因果関係
- 【時系列分析】課題1 為替レートの予測
- 「回帰分析から学ぶ計量経済学」を使ったセミナーを行います(2024年3月8日)
- 正誤表 回帰分析から学ぶ計量経済学















