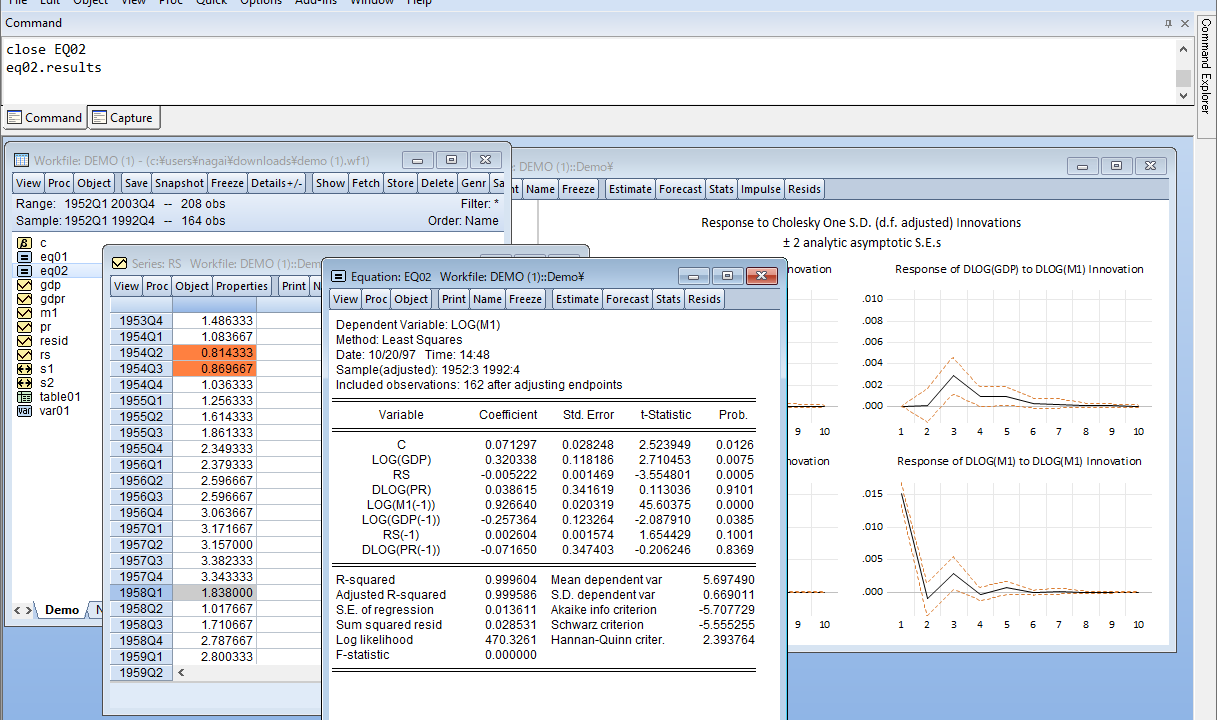
EViewsでのプログラムの書き方を説明します。
これを読めば簡単な回帰分析ができるようになります。
「経済統計の使い方」では、さまざまな分析手法の解説をしています。
EViewsのさまざまな使い方については、EViewsのまとめをご覧ください。

回帰分析
まず、回帰分析のプログラムについてです。プログラムというよりはコマンドですが、これが回帰分析の基本になります。最小二乗法はlsの後に変数を続けて書きます。定数項はCで表します。
最小二乗法
ls 被説明変数 c 説明変数
操作変数法
tsls 被説明変数 c 説明変数 @inst 操作変数
表
推定結果は、表の形で表すことが多いです。表を作成するには、
table table名
table名(1,1)= 数字
| (1,1) | (1,2) | … |
| (2,1) | (2,2) | … |
| : | : |
結果の保存
最小二乗法を推定すると、係数や決定係数など様々な変数が計算されます。これらはデータメンバーと呼ばれます。これらを表にすれば、分析結果がわかりやすくなります。
基本的には直前の推定を参照しますが、方程式名を明示的に書く方が安心です。以下は表の1行1列に、推定式の1番目の係数を入れた場合です。
equation 方程式名
方程式名.ls 被説明変数 C 説明変数
tab(1,1)=方程式名.@coefs(1)データメンバーの主要なものは以下になります。さらに詳しいものは下記記事を参照してください。
| 項目 | 記号 | 説明 |
| AIC | @aic | |
| 係数 | @coefs(i) | i番目の係数 |
| t値 | @tstats(i) | i番目の係数のt値 |
| 自由度修正済み決定係数 | @rbar2 | |
| サンプル数 | @regobs | |
| 係数の数 | @ncoef |

p値の計算
p値は直接参照できないので、t分布から計算します。
@tdist(t値,自由度)
具体的な計算式は以下の通りです。自由度は、サンプル数‐係数の数です。
@tdist( 方程式名.@tstats(i),@regobs-@ncoef)
期間を変えて推計
期間を変えて推計するには、tという変数を作成し、for next 文を使って繰り返し代入することで計算できます。推計期間を変えるには、単に数字を足せばよいので便利です。
以下の例では、最初のターンで1994年から2004年の期間で推計します。次は、1995年から2005年の期間で推計します。これを17まで繰り返します。
scalar t
for t=0 to 17
smpl 1994+t 2004+t
next
具体例
以下のデータを使って、推計期間をずらしながら計算した結果を示します。
1994年度から2021年度までの実質GDPと実質民間最終消費の年次データです。
scalar t
equation eqcp15
table tab
for t =0 to 17
smpl 1994+t 2004+t
eqcp15.ls cp15 c gdp15
tab(1+t,1)=eqcp15.@coefs(1)
tab(1+t,2)=eqcp15.@tstats(1)
tab(1+t,3)=@tdist(eqcp15.@tstats(1),@regobs-@ncoef)
tab(1+t,4)=eqcp15.@coefs(2)
tab(1+t,5)=eqcp15.@tstat(2)
tab(1+t,6)=@tdist(eqcp15.@tstats(2),@regobs-@ncoef)
tab(1+t,7)=eqcp15.@rbar2
next
この結果は以下の表になります。
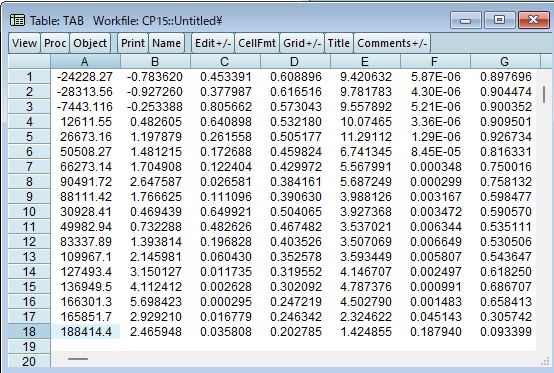
これをわかりやすく表側をつけると以下になります。
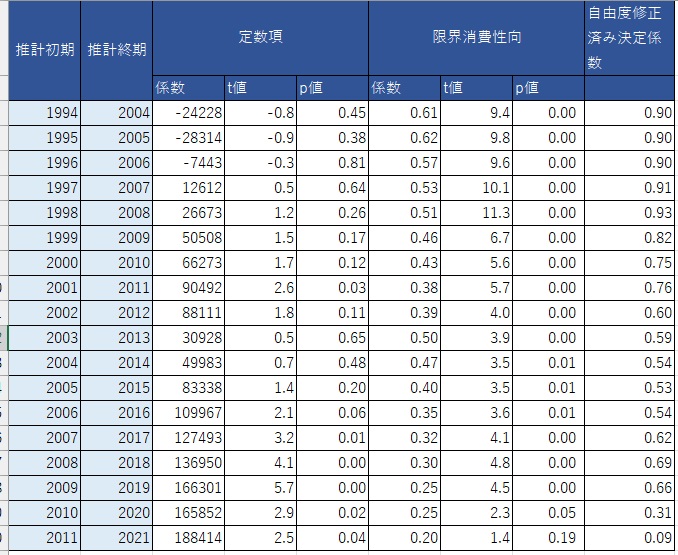
都道府県別に推計
都道府県別に同じ式を推定することもできます。
- 置換変数 {%X}
- コントロール変数 !counter
- サブルーチン subroutine
を使います。詳しくは以下を参照してください。

- 【時系列分析】課題3 ドリフト付きランダムウォーク
- 【時系列分析】課題2 グレンジャーの因果関係
- 【時系列分析】課題1 為替レートの予測
- 「回帰分析から学ぶ計量経済学」を使ったセミナーを行います(2024年3月8日)
- 正誤表 回帰分析から学ぶ計量経済学