母集団から抜き取った標本の分散(不偏分散)から、母集団の分散(母分散)を推定する方法です。不偏分散がχ(カイ)二乗分布に従うことを使って、推定します。
経済統計の使い方では、統計データの入手法から分析法まで解説しています。

不偏分散の分布
母集団の分散を$\sigma^2$とし、標本から計算した分散(不偏分散)を$U^2$とすると、以下の式は、自由度n-1のχ(カイ)二乗分布に従います。χは、ギリシャ文字のカイです。
$T=\dfrac{ (n-1)U^2}{\sigma^2}$
χ二乗分布
まず、χ二乗分布について説明します。標本平均を$\bar{X } $ 、母集団の分散を$\sigma^2$とすると、χ二乗分布はXを標準化したものの二乗和で表されます。
$ T=( \dfrac{X_1-\bar{X} }{\sigma})^2+( \dfrac{X_2-\bar{X}}{\sigma})^2 +\dots+(\dfrac{X_n-\bar{X}}{\sigma})^2 $
$ =\dfrac{(n-1)}{\sigma^2} \lbrack \dfrac{(X_1-\bar{x} )^2+(X_2-\bar{x})^2 + \dots +(X_n-\bar{X})^2)}{n-1} \rbrack$
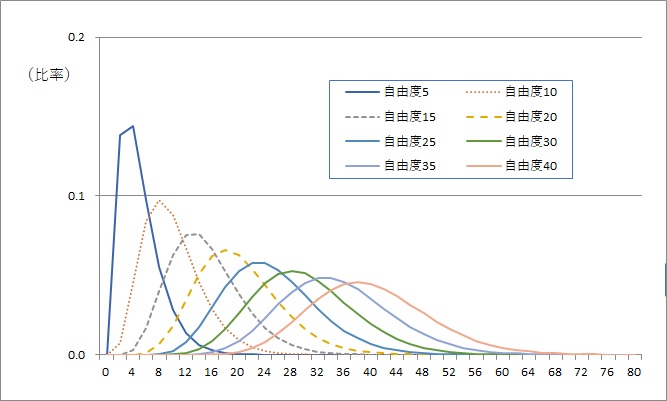
χ二乗分布の特徴
χ二乗分布には以下の特徴があります。
- 二乗和なので正の値
- 左右非対称
- 自由度で形が変わる
- 自由度を指定すれば形は決まる
χ二乗分布の信頼区間
χ二乗分布の信頼区間は、エクセルの関数で調べることができます。
$ CHISQ.INV(確率,自由度)$
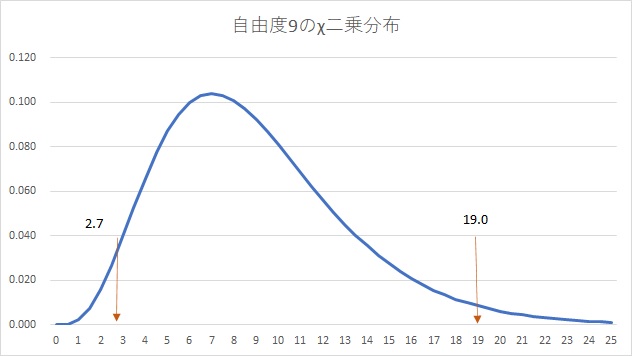
例えば、自由度9で95%信頼区間を調べる場合は、以下の関数を入力します。
$=CHISQ.INV(0.025,9)=2.7$
$=CHISQ.INV(0.975,9)=19.0$
95%の信頼区間は、2.7以上19.0以下だということがわかります。
区間推定の手順
•不偏分散($U^2$)を加工したものは、自由度n-1のχ二乗分布に従う。
•標本数10、信頼区間95%の場合、
$ 2.7≤ \dfrac{(n-1)U^2}{\sigma^2} ≤ 19.0 $
•その式を母集団の分散に関する式に変形する。
$ \dfrac{(n-1)U^2}{19.0}≤ \sigma^2≤ \dfrac{(n-1)U^2}{2.7} $
計算例
- サンプル数 10
- 標本平均 9.90
- 不偏分散 0.25
この時95%信頼区間で母分散を推定してみましょう。
不偏分散($U^2$)を加工したものは、自由度n-1のχ二乗分布に従います。
標本数10、信頼区間95%の場合、以下の式が成り立ちます。
$2.70≤ \dfrac{(n-1)U^2}{\sigma^2} ≤ 19.0$
この式を母集団の分散に関する式に変形します。
$ \dfrac{(n-1)U^2}{19.0} ≤ \sigma^2≤ \dfrac{(n-1)U^2}{2.7} $
答えは、母分散の95%信頼区間は0.118以上 0.833以下となります。
- 【時系列分析】課題3 ドリフト付きランダムウォーク
- 【時系列分析】課題2 グレンジャーの因果関係
- 【時系列分析】課題1 為替レートの予測
- 「回帰分析から学ぶ計量経済学」を使ったセミナーを行います(2024年3月8日)
- 正誤表 回帰分析から学ぶ計量経済学