【統計学】統計的検定の考え方｜やっかいですが、いろいろなことがわかります

経済統計の使い方では、統計データの入手法から分析法まで解説しています。

統計学・計量経済学のまとめ 統計学に関するまとめのサイトです。 回帰分析の基本 記述統計 記述統計の説明動画（エクセル） 平均 分...

仮説検定の手順

仮説検定には、統計学独特の論証法をします。

• 主張したいことと反対の仮説（帰無仮説）をたてます。
• 帰無仮説をもとに検定統計量を計算します。
• あらかじめ帰無仮説を棄却する水準を決めておきます。通常１％か５％です。
• 計算してでてきた検定統計量が棄却水準より大きければ帰無仮説を棄却します。
• または、検定統計量の出現する確率（p値）が棄却水準より小さければ、稀なことだとして棄却します。

帰無仮説を棄却するとは

帰無仮説を棄却する、というのはどういうことでしょうか。コインの裏表をあてることを観察して、予知能力があるかどうかを判定することを例にします。

コインの裏表を５回連続で当てた人がいる。この人に予知能力はあるか？

という問題を考えます。直感的には、予知能力がありそうだ、と思いますがどうでしょう？帰無仮説をたて、検定統計量を計算します。

•帰無仮説を「予知能力がない」とします。

•棄却域（通常ではありえないくらい小さい確率）を５％とします。

•検定統計量の計算です。ここでは、「予知能力がない」ことが前提なので、偶然５回連続で当たる確率を計算します。すると…

(1/2)^5=1/32=0.03125=３.125％

になります。

・通常ではありえないくらい稀な確率を５％と仮定したうえで、それより低い３％という数字が観察されました。５％ですら珍しいことなのに、さらに低い３％という稀な確率です。これは、帰無仮説である「予知能力がない」という前提が間違っていることを意味し、「予知能力がある」ということを否定できない、という結論になります。

ただ、棄却水準を１％とすると、「予知能力がない」という帰無仮説は棄却できず、「予知能力がない」という仮説が受容できることになります。

このように棄却域によって結論が変わるので、どの水準に棄却域を設定するのは非常に重要です。

帰無仮説と対立仮説

帰無仮説の反対の仮説として対立仮説があります。（両側検定）

• 帰無仮説(H₀)　μ＝０　　無に帰する仮説。棄却したい仮説。
• 対立仮説（H₁)　μ≠０

という関係が導け出せますが、対立仮説は、帰無仮説の否定の一部でもよいです。例えば以下の例です。（片側検定）

• 帰無仮説(H₀)　μ＝０
• 対立仮説（H₁)　μ＜０

片側検定の場合、μ＞０の場合は考えずに、棄却水準を決めるので、同じ棄却水準なら、両側検定の時よりも、棄却域が大きい（棄却しやすい）ことを示しています。

簡単にいうと、片側検定の方が主張が通りやすいです。

仮説検定（背理法に似ている）

仮説検定は、背理法に似ています。背理法とは以下のような論証法です。

$\sqrt{2}$が無理数であることを証明せよ

背理法では、以下のプロセスで、論証します。ちなみに、有理数とは$a/b$　(a,bは整数）で表されるものです。無理数は、$\pi$、$\sqrt{2}$、$\sqrt{3}$など、$a/b$で表されないものです。

• 「 $\sqrt{2}$が無理数である」を証明したい
• 「 $\sqrt{2}$が無理数である」を否定する、つまり「 $\sqrt{2}$が有理数である」という仮説を立てる
• 「 $\sqrt{2}$が有理数である」という仮定を立てたことで起こる矛盾を論証する
• 「 $\sqrt{2}$が有理数である」はおかしい、と言える
• 「 $\sqrt{2}$が無理数である」と言える

$\sqrt{2}$が無理数であることの証明

具体的な背理法の手順を示します。

$\sqrt{2}$が有理数であるとします。

このとき、 $\sqrt{2}$は整数ｍ、ｎを用いて、以下のように表せます。ただし、ｎは≠０です。

 $ \sqrt{２}  ＝ \dfrac{m}{n} $

両辺を二乗すると

 $ ２＝m^2／n^２　　⇔　　  ２n^2=m^2　　　$

この式の両辺を素因数分解したとき、左辺は素因数を奇数個持つのに、右辺は偶数個持ちます。矛盾が生じるので、 $\sqrt{２}$が有理数であるという仮定は否定されま、$\sqrt{2}$は無理数であるということになります。

背理法と仮説検定

背理法と仮説検定の類似性を示します。

背理法

• $\sqrt{２}$は有理数である（帰無仮説）
• $\sqrt{２}$は無理数である（対立仮説）
• $\sqrt{２}$を有理数であると仮定すると矛盾が生じる
• 仮定が間違い
• $\sqrt{２}$は無理数である

統計的検定

• 帰無仮説をたてる
• 対立仮説をたてる
• 帰無仮説を前提とした検定統計量が棄却域に入る
• 帰無仮説が間違い
• 対立仮説が正しい

なぜ仮説検定という方法をとるのか

母集団を調べれば、「ＡはＢである」という論証はできますが、標本からの論証だと不確かなところがあって断定的なことが言えないのが根本的な問題点です。

また、仮説検定では、重要な誤りを回避できます。「薬の効果がない」という帰無仮説を検定する場合、誤りを侵す確率（棄却水準）を分析者が設定できます。  

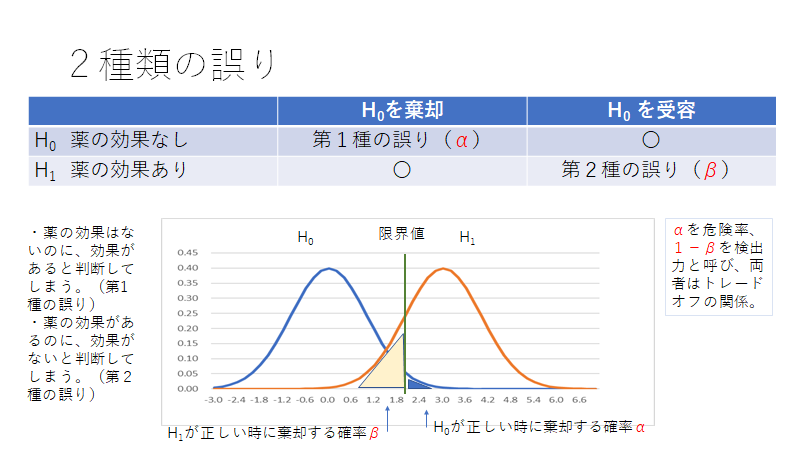
「薬の効果があるかどうかの検定」で可能性がある過ちには2種類あります。

• 第１種の誤り：薬の効果がないのに、あると判断してしまうこと
• 第２種の誤り：薬の効果はあるのに、ないと判断してしまうこと

この2つのうち、どちらが問題でしょうか？第1種の誤りの方が致命的です。この誤りを侵すと、重病人に対して効果のない薬を処方する可能性が出てくるからです。

仮説検定では、この誤りを侵す水準を決めることができます。もし厳密にこの誤りを減らそうとすると、棄却域を狭くする（例えば、棄却域を１％水準とする）ことで実現できます。

• 【時系列分析】課題３　ドリフト付きランダムウォーク
• 【時系列分析】課題２　グレンジャーの因果関係
• 【時系列分析】課題１　為替レートの予測
• 「回帰分析から学ぶ計量経済学」を使ったセミナーを行います(2024年３月８日）
• 正誤表　回帰分析から学ぶ計量経済学

検索

検索