【計量経済学】パネルデータの推定｜時系列データと横断面データの統合

パネルデータとは、時系列データとクロスセクション（横断面）データが両方あるものです。

時系列には2時点しかなくても、クロスセクションデータが多くあれば、両者を合わせてサンプル数を増やすことができます。

ただ、時系列データ、クロスセクションデータともに、個体別、時点別に違いがあるのかないのかを判別する必要があります。違いがあれば、それをダミー変数などで処理します。

経済統計の使い方では、統計データの入手法から分析法まで解説しています。

統計学・計量経済学のまとめ統計学に関するまとめのサイトです。回帰分析の基本記述統計記述統計の説明動画（エクセル）平均分...

Contents

パネルデータとは
プーリングモデル
固定効果モデル
変量効果モデル
差分法
まとめ

パネルデータとは

以下のデータはパネルデータの例です。データは高齢化比率とその後の10年間の成長率の平均です。時系列としては、1970年、1980年、1990年の3期間があり、クロスセクションとしては、カナダ、米国、英国、フランス、ドイツ、イタリア、日本の6つがあり、計18サンプルのものです。

	高齢化比率	成長率（その後10年の平均）	年
カナダ	7.90	4.26	1970
米国	9.84	3.26	1970
英国	12.94	1.94	1970
フランス	12.87	3.31	1970
イタリア	10.89	3.61	1970
日本	7.07	4.46	1970
カナダ	9.40	2.77	1980
米国	11.19	3.17	1980
英国	15.07	2.67	1980
フランス	13.97	2.47	1980
イタリア	13.15	2.26	1980
日本	9.04	4.09	1980
カナダ	11.27	2.84	1990
米国	12.39	3.26	1990
英国	15.72	2.30	1990
フランス	13.99	1.87	1990
イタリア	15.32	1.57	1990
日本	11.99	1.41	1990

横軸に高齢化比率、縦軸に成長率をとると以下のグラフになります。大まかには、高齢化比率が低いほど成長率が高いという分布になっています。

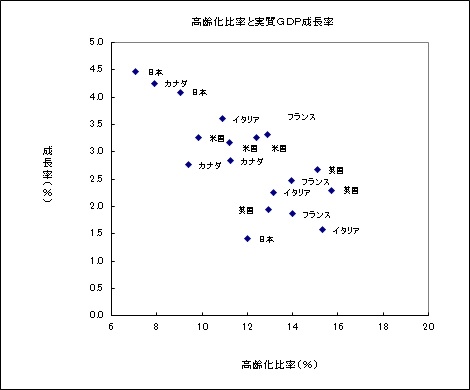
パネルデータを推計するには以下の方法が考えられます。クロスセクションごとの違いを考える場合は以下の分類になります。プーリングモデルは、国ごとに個別の効果がない場合に使います。固定効果は、国ごとに異なる効果がある場合に使います。変量効果も国ごとに異なる効果がある場合に使いますが、説明変数との相関が無い場合に使います。

$プール推計 Y_{it}= \alpha+ \beta X_{it} + e_{it} $

$固定効果 Y_{it}=\alpha_i + \beta X_{it} + e_{it} $

$変量効果 Y_{it}= \alpha + \beta X_{it}+ v_i + e_{it} $

時点ごとの違いに着目して、それぞれの効果を入れることもできます。

$プーリングモデル Y_{it}= \alpha+ \beta X_{it} + e_{it} $

$固定効果モデル Y_{it}=\alpha_{1i} + \alpha_{2t} + \beta X_{it} + e_{it} $

$変量効果モデル Y_{it}= \alpha + \beta X_{it}+ v_{1i} +v_{2t}+ e_{it} $

プーリングモデル

プーリングモデルは、すべてのデータを使って、定数項と係数を推計する方法です。個体差がない場合はこの推計で問題ありません。

$y=6.1-0.27x$

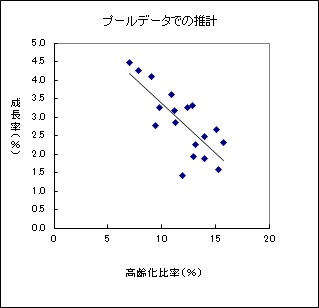
固定効果モデル

固定効果モデルによる推計は、ダミー変数による推計です。

固定効果は、個体差と時間による差の2通りが考えられます。国ごとに差があると考える場合は、国ごとにダミー変数を入力します。

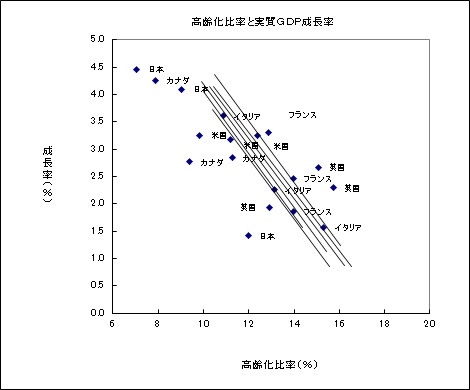
下のグラフは、個体効果ごとにダミー変数を入れた場合の推計値の例です。

$ y=-0.40x+7.15CAN+7.77USA+8.19GBR+8.08FRA+7.80ITA+7.12JPN $

CAN(カナダ)、USA(米国)、GBR(英国)、FRA(フランス)、ITA(イタリア)、JPN (日本)それぞれダミー変数です。

変量効果モデル

変量効果モデルは、個体効果がそれぞれ違うけれど、説明変数との相関が無いことを想定するものです。

$ Y_{it}= \alpha + \beta X_{it}+ v_i + e_{it} $

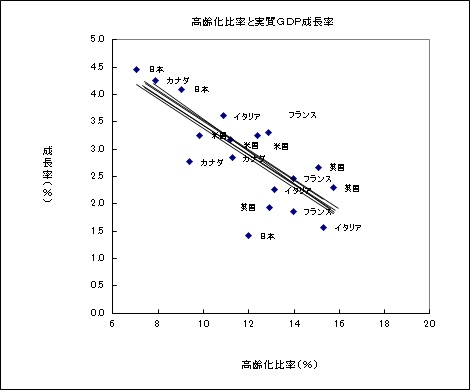
個体ごとの動きが確率変数$v_i$になっており、プーリングモデルに近いため、係数はプーリングモデルと固定効果モデルの間の値になります。この例では、個体効果の大きさは固定効果モデルに比べてかなり小さく推計されています。

$ y=6.17-0.28x-0.024CAN+0.018USA+0.017GBR-0.004FRAー0.025ITA+0.019JPN $

差分法

差分法は、因果推論をするために使うもので、個体別に効果を与える観察できない変数$A_i$（脱落変数）の効果を考慮するものです。パネルデータを推計する際に、説明変数、被説明変数とも差分で推計するものです。被説明変数に与える脱落変数の効果を除去することができます。被説明変数に影響をあたえるけれど、観察できない変数を$A_{i}$とすると、以下の式が考えられます。

$ Y_{it}=\alpha_i + \beta X_{it} + A_{i} + e_{it} $

1期前の式は以下の式になります。

$ Y_{it}=\alpha_i + \beta X_{it} + A_{i} + e_{it} $

差分をとると、$A_{it}$の効果を取り除くことができます。

$ \Delta Y_{it}= \alpha_i + \beta \Delta X_{it} + \Delta e_{it} $