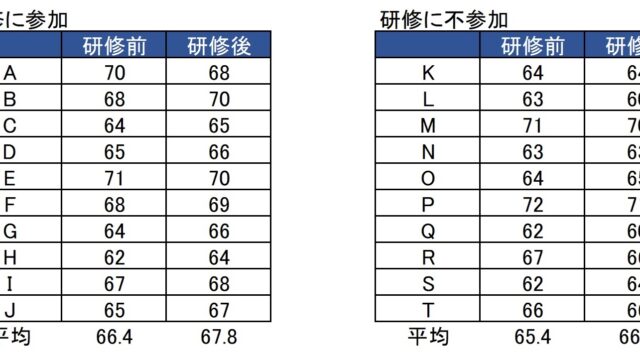
回帰分析は計量経済学の基本となるものです。変数に$Y_i=\alpha+\beta X_i$といった関係を付けます。
経済統計の使い方では、統計データの入手法から分析法まで解説しています。

回帰とは
回帰とは、もともと「元に戻る」という意味です。
イギリスの統計学者ゴールトン(1822-1911)のさやえんどうの観察から始まっています。表はゴールトンの観察結果です。大きな豆の子は親よりは小さくなり、小さな豆の子は親よりは大きくなる傾向があり、これを「平均への回帰(regression toward the mean)」と呼びました。
| 親 | 子(中心値) |
| 15 | 15.4 |
| 16 | 15.7 |
| 17 | 16.0 |
| 18 | 16.3 |
| 19 | 16.6 |
| 20 | 17.0 |
| 21 | 17.3 |
これは人間の身長にも当てはまり、背の高い親の子供には、親よりは少し低い身長の子供が生まれ、背の低い親の子供には、少し高い子供が生まれることが観察されました。
regression
回帰は英語ではregressionと言います。というか、regressionの訳が回帰です。
Rao教授によると、ゴールトンが使ったのは先祖返り(reversion)という言葉で、reversionが後になって回帰(regression)と呼ばれるようになったと書いてありますが、いつからそう呼ぶようになったのかは不明です。
まず彼は、親の身長が極端に高くなった場合、子供の身長の条件付き平均値は、親の身長から離れて全体の平均に近づく、先祖がえり(reversion)の現象を発見した。このreversionが後になって回帰と呼ばれれたもで、ゴールトンはその強さを表すための指標としてrを導入した。
C.Radhakrishna Rao 訳 柳井晴夫・竹内啓「多変量解析ーその起源と発展に関する回想ー」応用統計学Vol.12,No.2(1983)
regressionという言葉は、逆行とか退行などと訳される場合が多いですが、それに回帰という言葉を当てたのは素晴らしいと思います。
「原点への回帰」「伝統への回帰」などと使ったり、「南回帰線Tropic of Capricorn」「北回帰線Tropic of Cancer」という言葉もあり、回帰という言葉のイメージはいいです。
2変数の例
回帰分析は、複数の変数を関係づけるものです。まず、2つの変数で考えます。
$X_i$と$Y_i$のデータがあるとします。iはクロスセクション(横断面)データであれば、個人や企業を表す個体番号、時系列データであれば時刻を示します。
| i | $X_i$ | $Y_i$ |
| 1 | 4 | 4 |
| 2 | 8 | 5 |
| 3 | 12 | 6 |
| 4 | 2 | 1 |
| 5 | 6 | 3 |
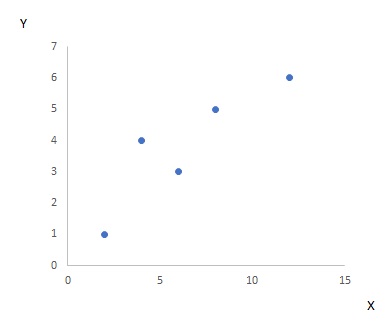
この2つのデータの関係を表す直線を考えると、以下の直線が考えられます。
$Y_i=\alpha+\beta X_i$
こうした式を作ることをYにXを回帰する、YのX上への回帰を求めるなどと言います。
両方の点になるべく近いように直接を引くと以下グラフになります。この直接の切片や傾きを求めるために、最小二乗法という方法を使います。
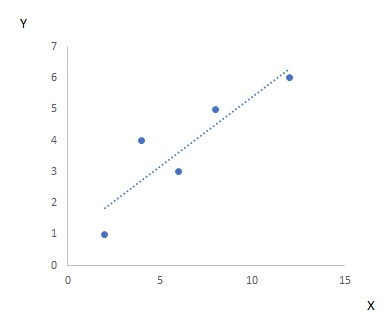
最小二乗法
最小二乗法による係数の求め方を説明します。
上のグラフのように変数の間に直線は引けますが、ぴったりと一致しているわけでないです。残差が生じています。残差を$u_i$とすると以下のように書けます。
$ u_i=Y_i-\alpha – \beta X_i $
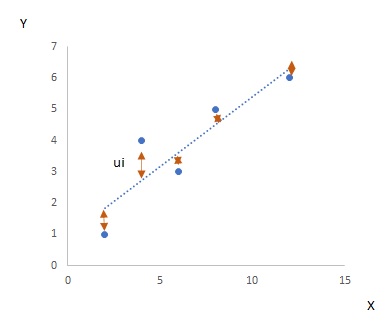
最小二乗法では、この残差の二乗和を最小にするように計算します。結果を載せると、以下の式になります。
$Y = 0.9459+0.4459X $
なぜ単純に誤差を最小にしないのでしょうか。誤差を単純にすべて加えると、プラスのものもマイナスのもあるので、ゼロに近い値になり、意味がありません。
誤差の絶対値を足して、それを最小にするという方法も考えられますが、絶対値は計算がやっかいなので、使われません。
エクセルによる具体的な回帰分析のやり方は、以下の記事を見て下さい。

説明変数と被説明変数
残差も含めて式に書くと以下のようになります。
$Y_i=\alpha+\beta X_i+u_i$
Y_iのことを被説明変数、Xiを説明変数と呼びます。回帰分析はさまざまな分野で使われているので、いろいろな呼び方がありますが、同じものです。
| 被説明変数 | 説明変数 |
| 従属変数 | 独立変数 |
| 応答変数 | 予測変数 |
| 目的変数 | 特徴量 |
- 【時系列分析】課題3 ドリフト付きランダムウォーク
- 【時系列分析】課題2 グレンジャーの因果関係
- 【時系列分析】課題1 為替レートの予測
- 「回帰分析から学ぶ計量経済学」を使ったセミナーを行います(2024年3月8日)
- 正誤表 回帰分析から学ぶ計量経済学