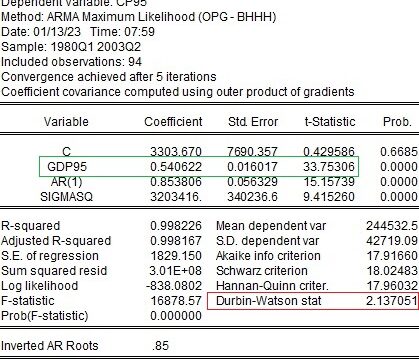
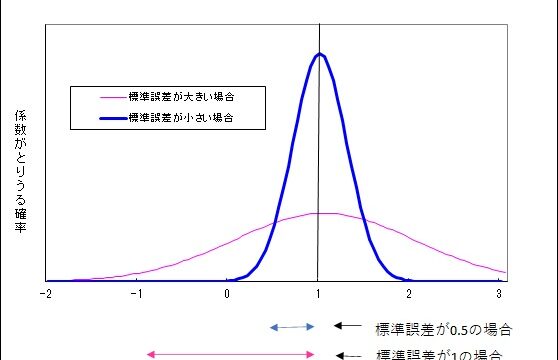
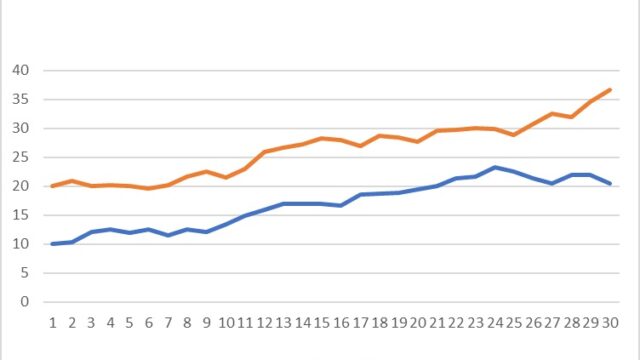
どういう時に使うんですか?
95%信頼区間を求めたりする時ですね。
経済統計の使い方では、統計データの入手法から分析法まで解説しています。


確率分布とは?
確率分布とは、ある確率変数のそれぞれの値に対する確率(連続変数の場合は確率密度ですが、確率と表記します)をグラフにしたものです。
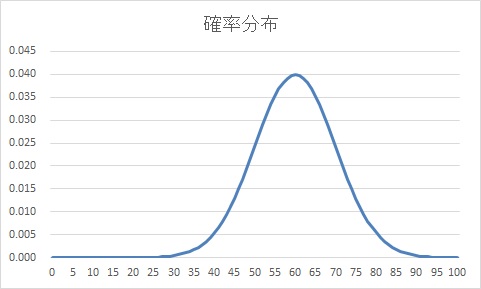
例えば、確率変数Xが試験の得点で、確率分布が正規分布に従うとした時のグラフは以下のようになります。平均点60点、標準偏差10点の場合です。
NORM.DIST関数
確率分布に関する計算はエクセルの関数を使うと便利です。
たとえば、
平均点が60点、標準偏差10点の時、80点の確率はいくらか
という問題に対しては、NORM.DIST関数を使います。最後の項目は、確率(密度)を出力する場合はFALSEにします。TRUEにすると、累積確率関数になります。
$ =NORM.DIST(調べる数,平均,標準偏差,FALSE)$
平均点60点、標準偏差10点の場合で、80点の確率を調べる場合は以下になります。
$ =NORM.DIST(80,60,10,FALSE)=0.005399 $
で計算できます。約5%です。
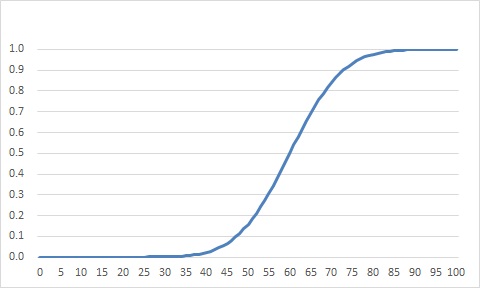
最後の項目をTRUEにすると、累積確率関数になります。
$ =NORM.DIST(80,60,10,TRUE)=0.97725 $
この試験で80点を取るということは、全学生を成績順に並べた場合、97.7%に位置することを意味します。
NORM.INV関数
また、
平均点が60点、標準偏差10点の時、有意水準が片側だけで5%の位置は何点になるか?
という問題に対しては、NORM.INV関数で計算できます。
$ =NORM.INV(確率,平均,標準偏差)$
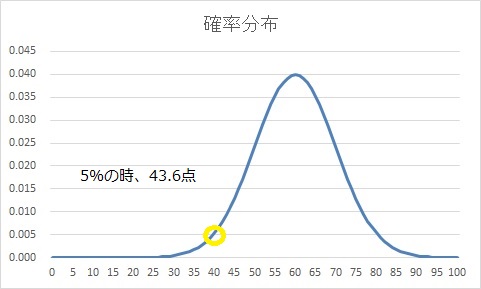
$ =NORM.INV(0.05,60,10)=43.55146 $
で計算できます。全学生の下位5%に入るのは、43.6点以下の学生だということを意味します。
その他の分布関数
その他の分布についても基本的には同じです。
| 分布関数 | 逆関数 | |
| 正規分布 | NORM.DIST() | NORM.INV() |
| t分布 | T.DIST() | T.INV() |
| χ二乗分布 | CHISQ.DIST() | CHISQ.INV() |

- 【時系列分析】課題3 ドリフト付きランダムウォーク
- 【時系列分析】課題2 グレンジャーの因果関係
- 【時系列分析】課題1 為替レートの予測
- 「回帰分析から学ぶ計量経済学」を使ったセミナーを行います(2024年3月8日)
- 正誤表 回帰分析から学ぶ計量経済学