次の表は、2人以上世帯の食器洗い機の普及率です。ロジスティック曲線を当てはめて、2050年までの普及率を予測してみましょう。
経済統計の使い方では、経済統計の入手法から分析法まで解説しています。

データ
以下の表が食器洗い機の普及率です。
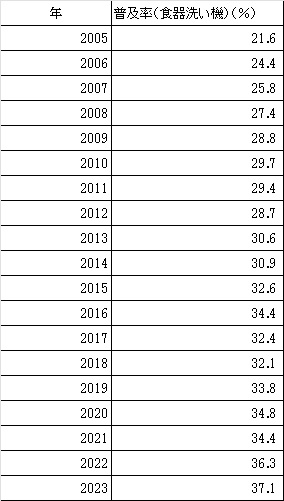
データは、内閣府の『消費動向調査』とったもので、毎年3月分に載っています。
統計表番号3総世帯の「主要耐久消費財等の普及・保有状況」にさまざまな耐久消費財の普及率が載っています。
ロジスティック曲線
ロジスティック曲線は以下の式で表されます。
$ Y_i=\dfrac{1}{1+e^{-X_i}} $
$\alpha$と$\beta$を使い、当てはまりを良くします。上記式は飽和点が1の場合ですが、飽和点をSとすれば以下の式です。
$ Y_i=\dfrac{S}{1+e^{-(\alpha+\beta X_i)}} $
$e=$の式になるように変形します。
$ \dfrac{Y_i}{S}=\dfrac{1}{1+e^{-(\alpha+\beta X_i)} } $
$ \dfrac{Y_i}{S}(1+e^{-(\alpha+\beta X_i)})=1 $
$ 1+e^{-(\alpha+\beta X_i)}=\dfrac{S}{Y_i} $
$ e^{-(\alpha+\beta X_i)}=\dfrac{S}{Y_i}-1 $
$ -(\alpha+\beta X_i)=log(\dfrac{S-Y_i}{Y_i}) $
対数をとります。
$ log(e^{-(\alpha+\beta X_i)})=log(\dfrac{S-Y_i}{Y_i}) $
$ -(\alpha+\beta X_i)=log(\dfrac{S-Y_i}{Y_i}) $
被説明変数、説明変数を以下のように加工すれば、最小二乗法で推定できます。
$ -log(\dfrac{S-Y_i}{Y_i}) =\alpha+\beta X_i $
被説明変数をエクセルで加工するには、$-1*ln((S-Y_i)/(Y_i))$と入力します。
説明変数$X_i$は西暦とし、Sは飽和点なので、100として計算します。
推定結果は以下のようになります。
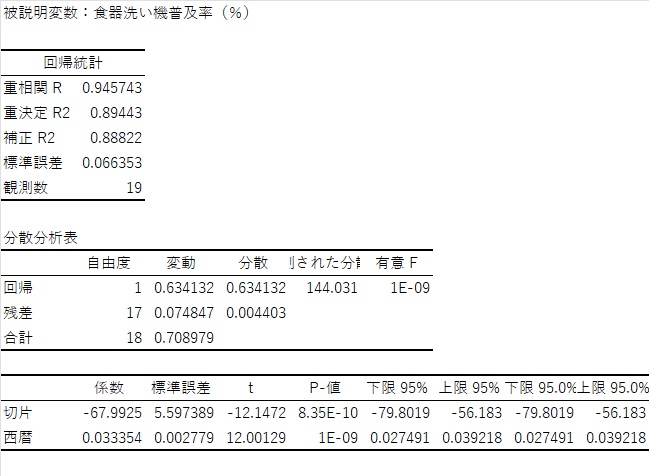
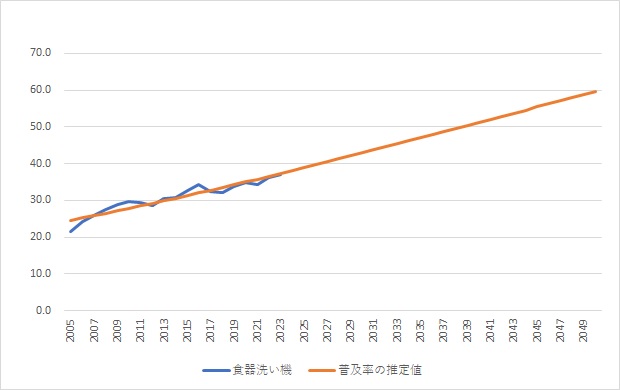
実績値と2050年までの普及率予測値のグラフです。
- 【時系列分析】課題3 ドリフト付きランダムウォーク
- 【時系列分析】課題2 グレンジャーの因果関係
- 【時系列分析】課題1 為替レートの予測
- 「回帰分析から学ぶ計量経済学」を使ったセミナーを行います(2024年3月8日)
- 正誤表 回帰分析から学ぶ計量経済学