経済指標には、季節性を持ったものが多いです。季節性は天候、年中行事、慣行などから生まれてきます。そのままのデータだと季節変動が大きくて、実態を把握することができません。季節性を除く方法を考えます。
季節性を除くには、前年同期比をみることが一つの方法です。前年の同じ期なら季節性も同じだからです。
もう一つは季節調整値を作る方法です。系列に移動平均をとることで、季節変動がならされます。前年同期比に比べて、季節調整値は、直近の動きを把握するうえで便利な指標です。
経済統計の使い方では、統計データの入手法から分析法まで解説しています。

季節性とは
経済指標は、季節性を持ったものが多いです。季節性の要因としては以下のものが挙げられます。
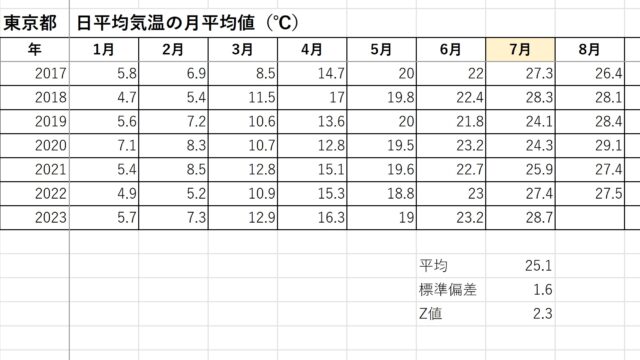
- 天候要因 気温や降雨量・降雪量は経済活動に直接影響を与えます。気温が上がれ夏には、アイスクリームやビールの消費が増え、冬にはスキーなどのウインタースポーツへの支出が増えます。
- カレンダー要因 1ヵ月の日数や祝日の数の違いです。年末年始、ゴールデンウィーク、お盆など、休日が続くと、工場の稼働日数が少なくなり、生産が減ります。2月は他の月よりも日数が少ないので、生産が少なくなります。一方、小売店の売り上げは休日が増えると増えます。
- 制度・習慣要因 夏にはお中元、12月にはお歳暮の習慣があります。ボーナスが支給される7月や12月には消費が増えます。
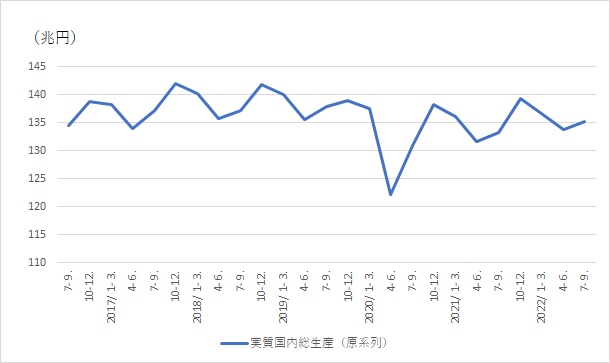
実質GDPの原系列も季節性があります。最も経済活動が高まるのは10-12月期で、最も低いのは4-6月期です。クリスマスなどのイベントがあり、ボーナスが支給されるため、10-12月の経済活動が活発だということでしょう。
前年同期比
季節性のあるデータは、季節変動が大きいため、趨勢的に増えているのか減っているのかがわかりにくいです。最も簡単に季節性を除く方法は、前年同期(前の年の同じ期)と比べることです。当期が10-12月期なら前年の10-12月期と比べるということです。前年同期比は以下の式で計算できます。月次データの場合は前年同月比ともいいます。
$ 前年同期比=\dfrac{今期の値-前年同期の値}{前年同期の値}×100 $
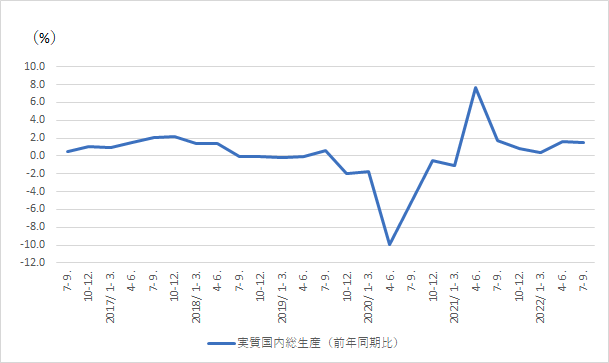
季節調整値
季節性を除く方法として、季節調整値を使う方法があります。季節調整にはさまざまな方法がありますが、政府が採用しているのは米国商務省センサス局が開発したX12-ARIMAです。
四半期の場合、基本的には4四半期(1年)分の移動平均をとることで季節性を取り除くことができます。ただ、中心移動平均をとる場合、当期が真ん中にあるので、奇数期の移動平均をとる必要があります。
X12-ARIMAでは、ヘンダーソン移動平均を使って、加重平均しています。ウエートは以下のようになっています。真ん中が当期です。
-0.073, 0.294, 0.558, 0.294, -0.073
たとえば、2020年1-3月期の場合は、2019年7-9月期の値に-0.073をかけ、2019年10-12月期の値に0.294をかけ、2020年1-3月期の値に0.558をかけ、2020年4-6月期の値に0.294をかけ、2020年7-9月期の値に-0.073をかけ、すべて足します。
ウエートをすべて加えると1になります。月次には月次のウエートがあります。
実質GDPに関してヘンダーソン移動平均を計算すると、以下のグラフのようになります。これが季節調整値の基本的な形です。
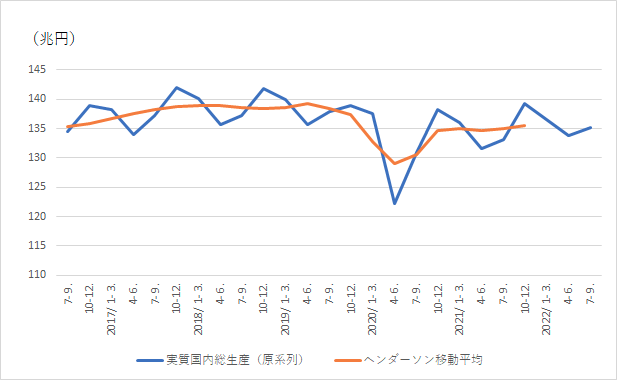
しかし、中心移動平均をとっただけでは、最も知りたい最新の数字がわかりません。5期中心移動平均をとるためには現在より2期先までのデータが必要になります。
X12-ARIMAでは、将来の値をARIMAモデルで予測して、それを使って季節調整をします。ARIMAモデルについては以下を参考にしてください。
季節調整自体は移動平均でおおむね達成できますが、政府が発表する季節調整値は、ARIMAモデルによる予測のほか、曜日調整、うるう年調整、不規則変動の調整などさまざまな微調整を行っています。
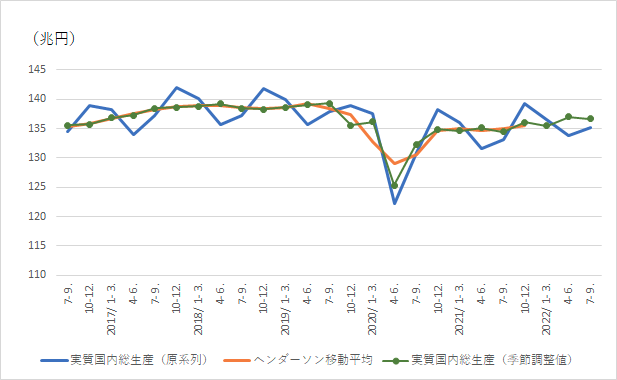
最終的な内閣府が発表した季節調整値は以下の緑の線になります。
前年同期比との違いを考えると、前年同期比は動きがゆっくりとしていて趨勢をとらえるにはいいと思います。季節調整値の前期比は、直近の動きを細かく捉える場合に向いています。
X12-ARIMAについてさらに詳しく知りたい方は以下の記事を参考にしてください。
まとめ
- 経済指標には季節性があります
- 季節性を除くには前年同期比をみることが有効です
- 季節調整値を使うと、直近の動向が細かく把握できます
- 【時系列分析】課題3 ドリフト付きランダムウォーク
- 【時系列分析】課題2 グレンジャーの因果関係
- 【時系列分析】課題1 為替レートの予測
- 「回帰分析から学ぶ計量経済学」を使ったセミナーを行います(2024年3月8日)
- 正誤表 回帰分析から学ぶ計量経済学