【統計学】【エクセル】平均値の差の検定（母分散が等しくない場合）

経済統計の使い方では、統計データの入手法から分析法まで解説しています。

【エクセル】エクセルのまとめ 経済統計の使い方では、統計データの入手法から分析法まで解説しています。 https://officekaisuiyoku.com...

統計学・計量経済学のまとめ 統計学に関するまとめのサイトです。 回帰分析の基本 記述統計 記述統計の説明動画（エクセル） 平均 分...

平均値の差の検定（母分散が等しくない場合）

2つの平均値に差があるかどうかの検定です。

今回の条件は、母平均は等しいが、母分散が等しくない場合です。

同じ母平均の母集団Ａ、Ｂからそれぞれ大きさ$n_A$、$n_B$の標本を抽出したとします。このとき、Tは自由度ν（ニュー）のｔ分布に近似的に従います。

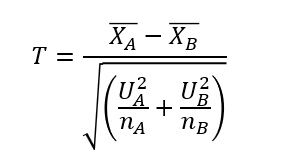
ただし、ν（ニュー）は以下の式で求めます。わかりにくいですが、一番下の文字は$n_A$から１を引いたもの、$n_B$から１を引いたものです。

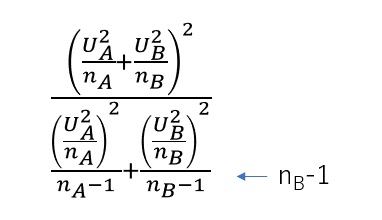
エクセルでの計算は簡単

等分散を仮定した時と同じ例を、エクセルで計算してみましょう。

金融業と製造業の年間収入に差があるかどうかを５％水準で検定する場合を考えます。データは以下の通りとします。金融業から10人、製造業から10人をランダムに選んできて年収を聞いたデータです。

2つの母集団の分散は異なるものとします。

金融業	製造業
744	672
684	708
780	672
720	684
756	696
696	684
684	720
720	660
720	684
696	660

【エクセル】分析ツールの有効化｜オプションの設定を変更します。 記述統計量の出力や回帰分析など統計分析をするには、エクセルのアドイン（追加プログラム）である「分析ツール」を有効化する必要があります...

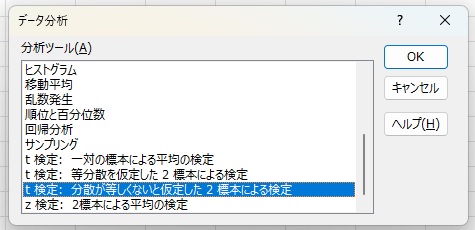
エクセルで平均値の差の検定をする場合は、分析ツールを使います。データ→データ分析で、分析ツールが表示されます。分析ツールのなかのｔ検定：等分散を仮定した2標本による検定を選びます。

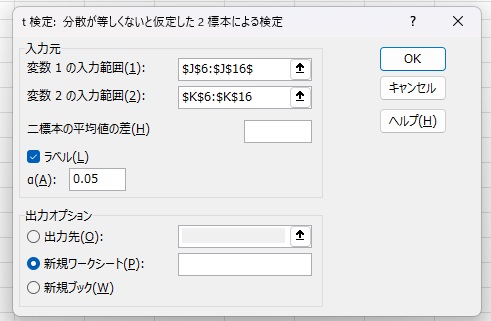
変数1と変数2を指定します。ラベル（変数名）がある場合はラベルにチェックします。棄却域は５％となっています。

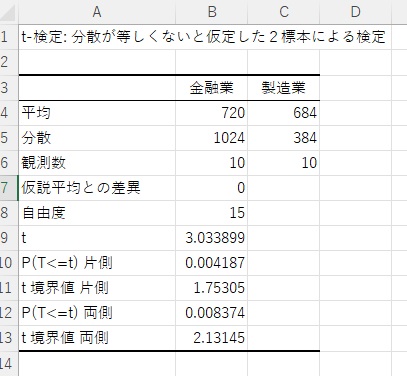
以下のように出力されます。ｔ値は3.033899です。５％水準の棄却域は両側検定で2.13145が境界値となります。この結果から、帰無仮説は棄却できることがわかります。つまり、金融業の賃金は製造業の賃金より有意に高いということです。

【エクセル】平均値の差の検定（対応がある場合） 平均値の差の検定 平均値の差の検定には以下の3種類が考えられます。 研修前、研修後など対応のある場合 母分散が等しい場合...

【統計学】【エクセル】平均値の差の検定（母分散が等しい場合） 平均値の差の検定 平均値の差の検定のうち、母分散が等しい場合です。 研修前、研修後など対応のある場合 母分散が等しい場合...

• 【時系列分析】課題３　ドリフト付きランダムウォーク
• 【時系列分析】課題２　グレンジャーの因果関係
• 【時系列分析】課題１　為替レートの予測
• 「回帰分析から学ぶ計量経済学」を使ったセミナーを行います(2024年３月８日）
• 正誤表　回帰分析から学ぶ計量経済学

検索

検索