最小二乗法が最適な推定値になるにはさまざまな条件がありますが、その一つに、「誤差の分散が均一である」があります。これが満たされない場合を不均一分散と呼びます。係数の標準偏差を計算する過程で、この仮定を使うため、この仮定が満たされないと、正しい係数の標準偏差が計算できないことになります。
通常の最小二乗法ではt値が小さめに計算されるので、本来有意なものを有意でないと判断する危険性があります。
この記事では不均一分散とは何か、どのように対処したらよいかをわかりやすく解説します。
経済統計の使い方では、統計データの入手法から分析法まで解説しています。

不均一分散の例
標準的な最小二乗法では以下の式が成り立っています。
$ Y_i=\alpha + \beta X_i + e_i $
このケースでは、誤差の分散の均一を仮定しています。
誤差の不均一分散の例としては、たとえば、$X$の値に応じて誤差が増える場合を考えます。$e_i$は$-1~1$で平均0、標準偏差1の正規乱数とします。
$u_i=\dfrac{X_ie_i}{10}$
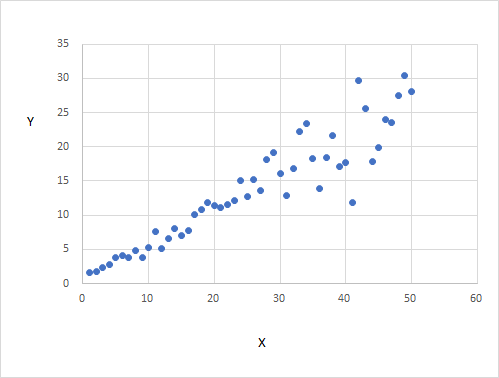
$X$を1から50とし、それに対応する誤差を$u_i=\dfrac{X_ie_i}{10}$とします。$Y_i$を$1+0.5X_i+u_i$として計算すると、$X_i$と$Y_i$の散布図は以下のようになります。$X_i$が大きくなると、$Y_i$の値は大きく上下に振れています。不均一分散の場合の$Y_i$と$X_i$の動きです。
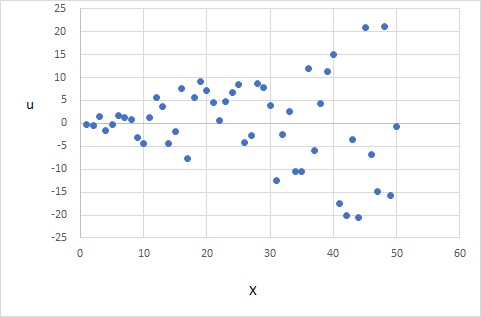
また、$X_i$と$u_i$の散布図は以下のようになり、$X_i$が大きくなると$u_i$も大きくなり、誤差が均一な分散でないことがわかります。
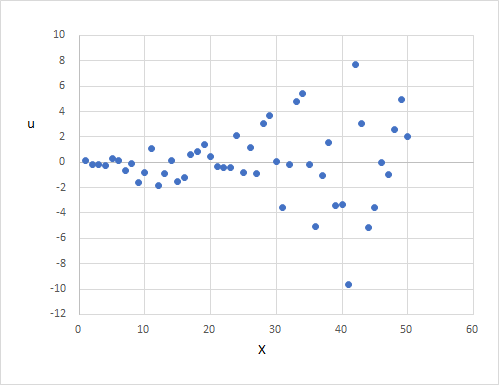
不均一分散の問題点
不均一分散の問題点は、係数の推定値にあるのではなく、係数の分散にあります。不偏性と一致性は満たされますが、効率性(分散が最も小さい性質)が満たされません。この場合、以下の推論から、最小二乗法によるt値は小さめに計算されることになります。
- 通常の最小二乗法による係数の標準誤差は最小ではない
- 真の係数の標準誤差はもっと小さい
- t値は係数/標準誤差で計算するので、真のt値はもっと大きいはず
- 通常の最小二乗法ではt値は小さめに計算される
誤差の分散が均一な場合は以下の式で表せます。
$ V(b)=\dfrac{\sigma^2}{\Sigma (x_i-\bar{x})^2}$
一方、誤差の分散が不均一の場合は、均一の分散$\sigma^2$が使えないため、$\sigma^2_i$とし、以下の式となります。係数の標準誤差やt値は、本来はこちらの式で推定する必要があります。
$ V(b)=\dfrac{\Sigma(x_i-\bar{x})^2\sigma^2_i}{(\Sigma (x_i-\bar{x})^2)^2}$
不均一分散の検定
不均一分散の検定の一つにホワイトの検定があります。誤差の二乗が説明変数や説明変数の二乗と相関があるかどうかを検定するものです。まず、通常の最小二乗法を適用します。
$ Y_i=\alpha + \beta X_i + e_i $
次に誤差の二乗を定数項と$X_i^2$、$X_i$に回帰します。
$ e_i^2=\alpha + \beta_1 X_i^2 + \beta_2 X_i + u_i $
$X_i^2$や$X_i$に係る係数が有意なら不均一分散があると判定します。
つまり帰無仮説 $ \beta_1=\beta_2=0 $に関してF検定をします。
不均一分散への対処
不均一分散に対処する方法として、標準誤差を計算しなおすという方法があります。不均一分散があったとしても、最小二乗法で推定した係数は不偏推定量で問題ありません。問題なのは係数の標準誤差なので、その計算法を工夫するということです。ホワイトの推定量(ロバスト標準誤差)などが考案されています。
ホワイトの推定量は、不明な$\sigma^2_i$の代わりに推計残差$ u_i=\hat{Y} – \alpha -\hat{\beta}X_i $の二乗を使うもので、以下の式で表されます。
$ V(b)=\dfrac{\Sigma(x-\bar{x})^2 u_i^2}{(\Sigma (x_i-\bar{x})^2)^2}$
通常、ホワイトの推定量の標準誤差の方が大きくなり、t値は小さくなります。
通常の最小二乗法は、効率的ではないので、標準誤差はさらに小さいものがあるはずです。しかし、真の分散の構造がわからないことを前提として、不均一分散があったとしても頑健な推定量という意味では、標準誤差は大きくならざるを得ないということでしょう。
加重最小二乗法
不均一分散の原因がわかっている場合に有効なのが、加重最小二乗法です。たとえば、冒頭の例のように、誤差が説明変数$X_i$の大きさに比例している場合です。この場合、被説明変数、説明変数ともに、$X_i$で割れば誤差は均一分散になります。式で書けば以下のようになります。これを推計すると係数の分散が正しいものになります。
$ Y_i=\alpha + \beta X_i + e_i $
$ \dfrac{Y_i}{X_i}= \dfrac{\alpha}{X_i} + \beta \dfrac{X_i}{X_i} + \dfrac{e_i}{X_i} $
$ \dfrac{Y_i}{X_i}= \alpha \dfrac{1}{X_i} + \beta + \dfrac{e_i}{X_i} $
EViewsで計算
Xに比例する誤差をそのまま使って、YをXに回帰する
通常の最小二乗法で推定した場合です。$\beta$に注目すると、係数は0.508、標準誤差は0.028419、t値は17.89974となります。
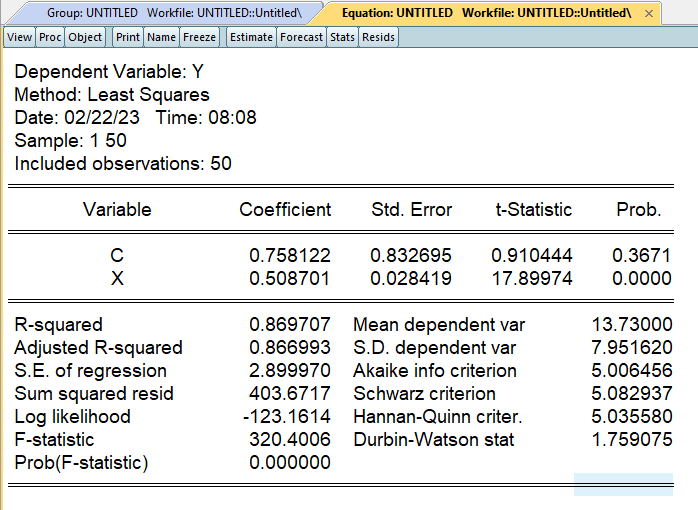
ホワイトの検定
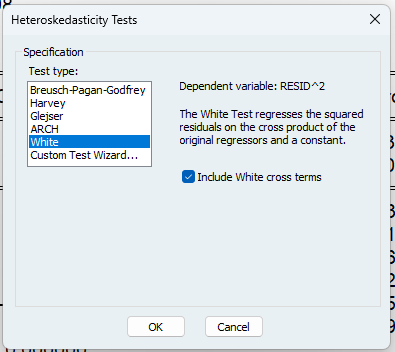
ホワイトの検定では、残差の二乗を説明変数と説明変数の二乗で回帰しています。ホワイトテストを実行するには、方程式オブジェクトのviewメニューを使います。
[View]→[Residual Diagnostics]→[Hetroskedasticity Tests…]
でwhiteを選びます。
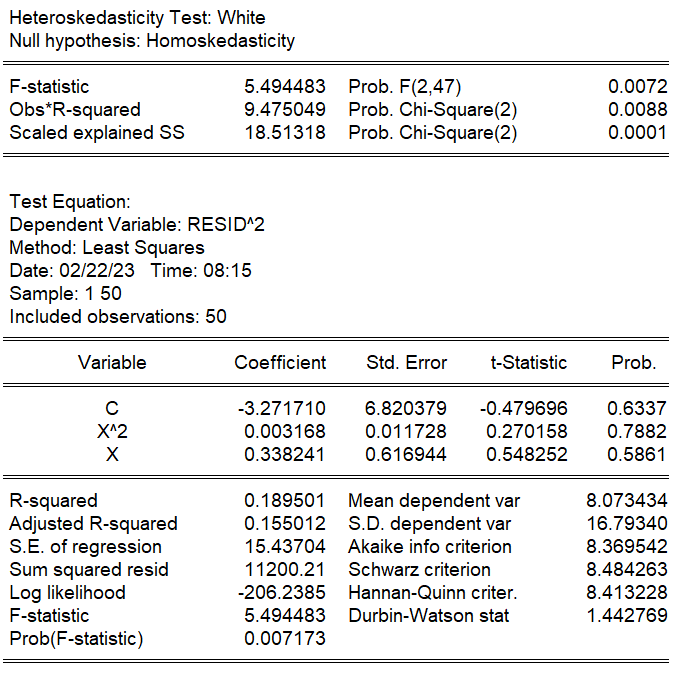
「係数がゼロである」という帰無仮説に対応するF値は5.494483で、p値は0.0072なので、1%の有意水準で帰無仮説は棄却されます。説明変数が誤差に影響を与えており、不均一分散があることがわかります。
ホワイトの推定量
ホワイトの推定量を使うと、推定値$\beta$は通常の最小二乗法から以下のように変わります。係数は同じですが、標準誤差が大きくなり、t値が小さくなります。
- 係数 0.508701→0.508701
- 標準誤差 0.028419→0.029333
- t値 17.89974→17.34245
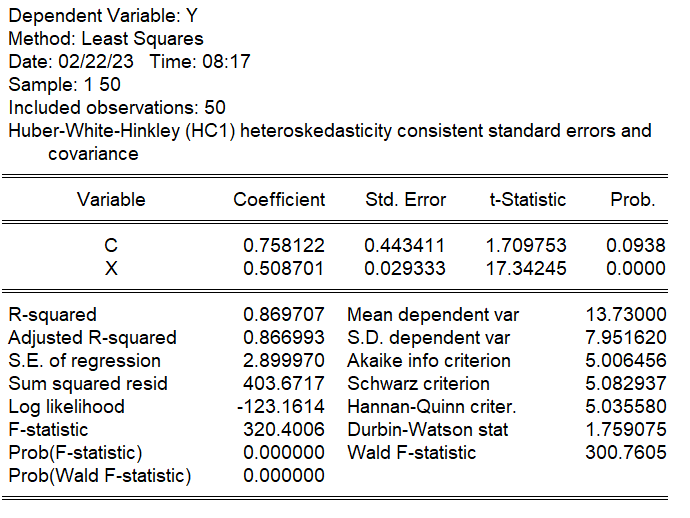
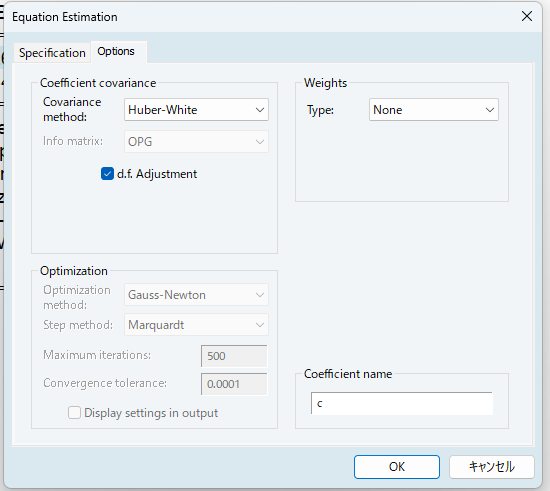
EViewsでホワイトの推定量を計算するには、方程式の変数を入力する画面で、[option]→Coefficient covarianceのcovariance method: で、Huber-Whiteを選びます。
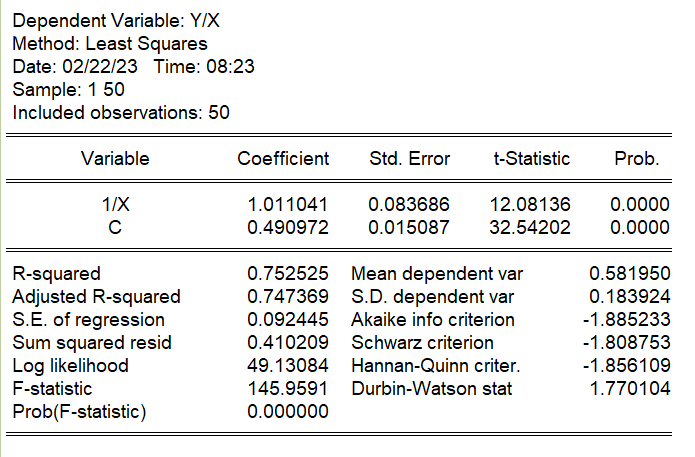
加重最小二乗法
加重最小二乗法の場合の結果です。データはもともと$Y_i=1+0.5X_i$として作っているので、最も近い推定結果になっています。最小二乗法の結果と加重最小二乗法の結果の比較です。
- 係数 0.508701→0.490972
- 標準誤差 0.028419→0.015087
- t値 17.89974→32.54202
その他の問題と解決法についてはこちら