経済統計の使い方では、統計データの入手法から分析法まで解説しています。
比率の標本から比率を推定する
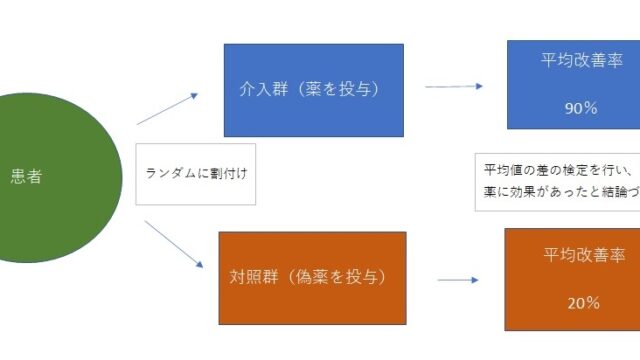
母集団に、リンゴが好きな人と嫌いな人がいるとき、「リンゴが好きな人の比率」（母比率）を標本の比率から推定します。
$X_i$は１か0をとるものとする。
通常の確率変数は、さまざまな値をとることができます。たとえば、サイコロの場合は、$X_i$は1～６を取ります。今回は、$X_i$が２つの値しかとらない場合です。起こる($X_i＝１$)か起こらない($X_i＝０$)かの2択の分布を考えます。これは、コインの表と裏、動物の雄と雌などのデータです。
確率ｐで１、確率（１－ｐ）で０となるとき、$X_i（i=1,2,3…n)$はベルヌーイ分布に従います。
- ベルヌーイ分布
- 平均$ｐ$
- 分散 $p(1-p)$
また、nが十分大きい時、標本平均（R)は、中心極限定理により、平均$p$、分散$p(1-p)／ｎ$の正規分布に従います。
区間推定の手順
nが十分大きい時、標本平均（R)は、中心極限定理により、平均p、分散p(1-p)／ｎの正規分布に従います。
信頼区間95％の場合、以下の式が成り立ちます。
$-1.96 ≤ \dfrac{R-p}{\sqrt{\dfrac{p(1-p)}{n}}} ≤ 1.96$
標本平均（R)と信頼区間の関係を式で表します。
$p－1.96\sqrt{\dfrac{p(1-p)}{n}}≤R≤p+1.96 \sqrt{\dfrac{p(1-p)}{n}}$
その式を母集団の平均に関する式に変形します。
$R－1.96 \sqrt{\dfrac{p(1-p)}{n)}}≤p≤R+1.96\sqrt{\dfrac{p(1-p)}{n}}$
ｎが十分大きい時、p（母集団の平均）はR（標本平均）で近似できます。（大数の法則）
$R－1.96\sqrt{\dfrac{R(1-R)}{n}}≤p≤R+1.96 \sqrt{\dfrac{R(1-R)}{n}}$
計算例
あるYou tubeのサイトの認知率を大学生400人にきいたところ、320人が知っていた。この場合、日本全体の認知率は95％の信頼区間で何％から何になるか？
$R－1.96\sqrt{\dfrac{R(1-R)}{n}}≤p≤R+1.96 \sqrt{\dfrac{R(1-R)}{n}}$
- 母集団はｐ
- 標本平均Rは320／400＝0.8
- 標本数nは400
なので、以下の式となります。
0.7608≤p≤ 0.8392
つまり、認知率は76％以上83％以下です。
- 経済学Q＆A（試験編）
- 【経済統計】消費をみるために必要な月次指標ベスト３｜消費総合指数、商業動態統計、家計調査
- 経済統計チャットボット マホナ
- 経済金融指標の見方 Q&A２
- 経済金融指標の見方 Q&A
