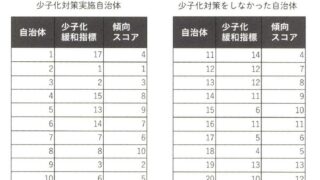
操作変数法の例で使った就学年数と年収の関係について、Excelの「分析ツール」を使って実際に推定してみて下さい。
(1)現実には不可能な、個人の能力のデータが入手できた場合の推定
$年収=\alpha+\beta_1 × 就学年数+\beta_2× 個人の能力$
(2)操作変数を使った1段階目の推定
$就学年数=\alpha + \beta ×大学までの距離$
(3)操作変数を使った2段階目の推定
$年収=\alpha +\beta ×就学年数の推定値$
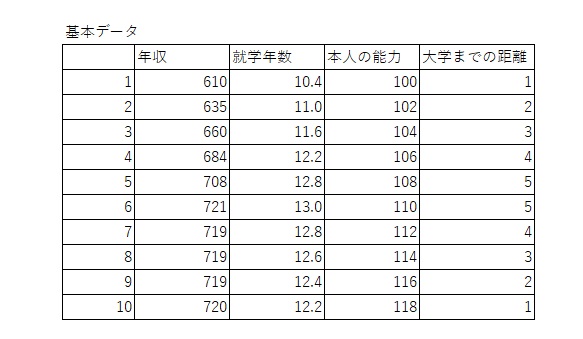
まず、教科書で使ったデータは以下の表です。ダウンロードできます。
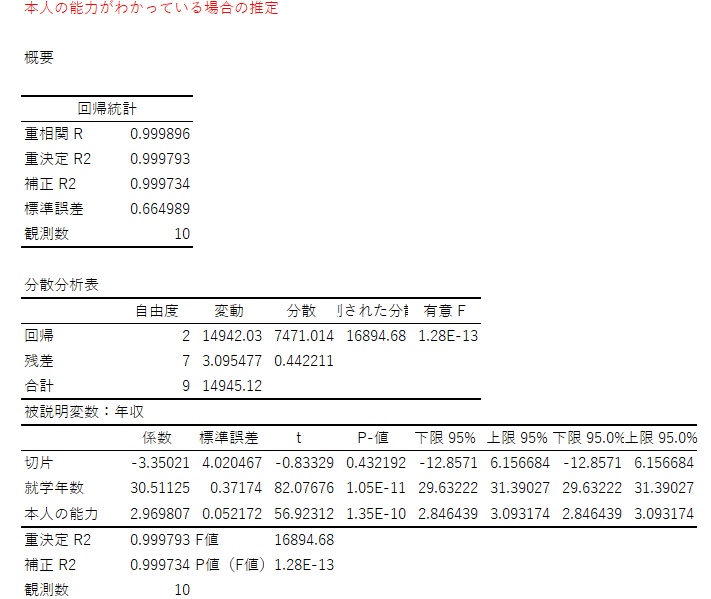
現実には不可能な、個人の能力のデータが入手できた場合の推定
被説明変数を年収、説明変数を就学年数と本年の能力として推定します。この係数が真の値に近いことになります。就学年数の係数は30.51です。
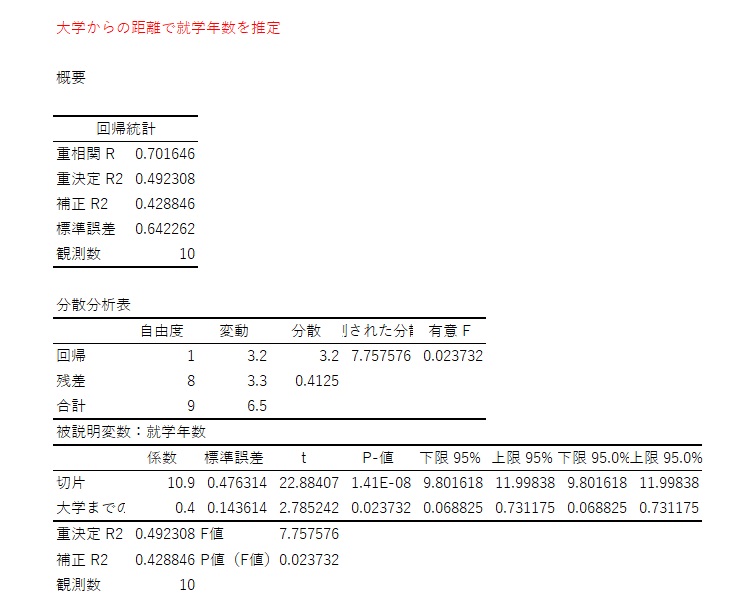
操作変数を使った1段階目の推定
次は、操作変数で就学年数を推定します。就学年数の内生性を取り除くための推計です。
分析ツールで回帰分析を行うとき、残差にチェックを入れておけば、次の推計で使う周が億年数の推計値（予測値と表示される）も計算されます。
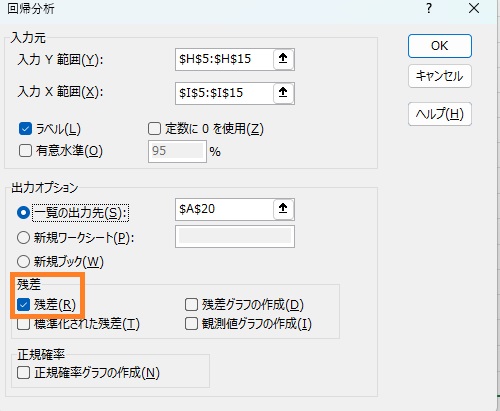
推定結果は以下の通りです。
操作変数を使った2段階目の推定
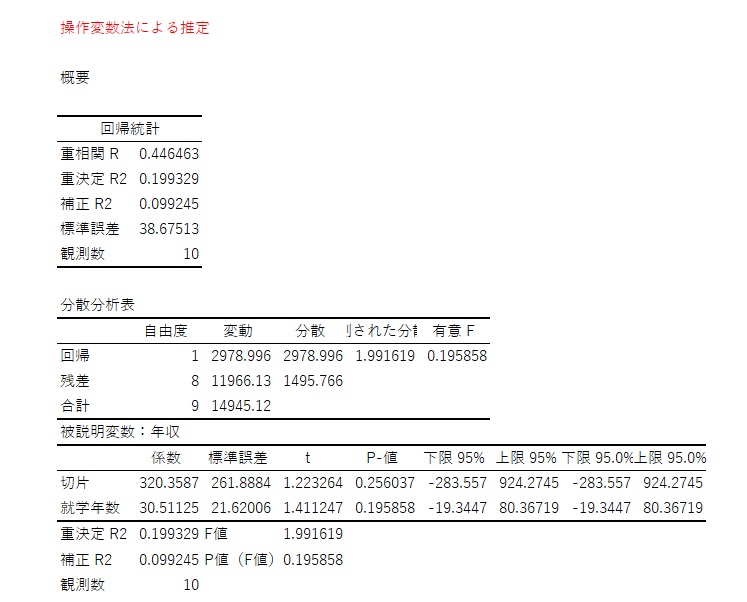
被説明変数を年収、１段階目の推定で作成した推定値を説明変数として推定します。就学年数の係数は30.51で、真の値の推定値30.51と一致することが分かります。
経済統計の使い方では、経済統計の入手法から分析法まで解説しています。
統計学・計量経済学のまとめ
統計学に関するまとめのサイトです。
教科書
「回帰分析から学ぶ計量経済学－Excelで読み解く経済の仕組み」
回帰分...
- 経済学Q＆A（試験編）
- 【経済統計】消費をみるために必要な月次指標ベスト３｜消費総合指数、商業動態統計、家計調査
- 経済統計チャットボット マホナ
- 経済金融指標の見方 Q&A２
- 経済金融指標の見方 Q&A
スポンサーリンク
スポンサーリンク
