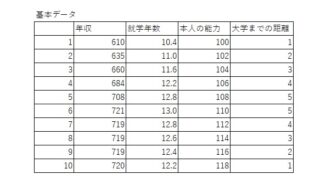
自治体が行った少子化対策の効果を見るための課題です。l～20までの自治体に
ついて、合計特殊出生率などを使って、少子化緩和指標が測れたものとします。指
標が高いほど、少子化緩和効果が高いとします。ただし、自治体1～10は少子化対
策を実施し、自治体1～ 20までは少子化対策を実施しなかったとします。傾向スコ
アは、人口や経済構造などから測ったもので、少子化対策の実施傾向が似ているこ
とを示します。これらのデータから少子化対策は効果があったと判断できるでしょうか。傾向スコアマッチングの手法を使って分析して下さい。
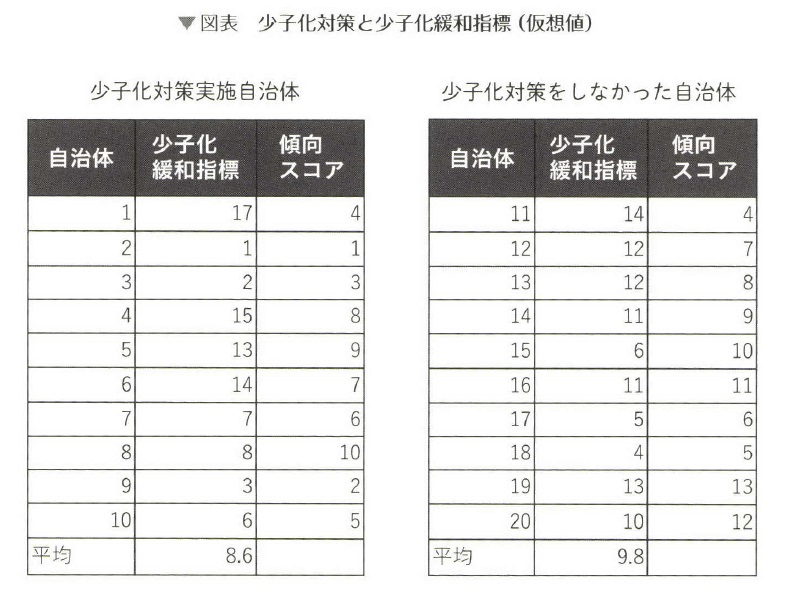
傾向スコアを揃える
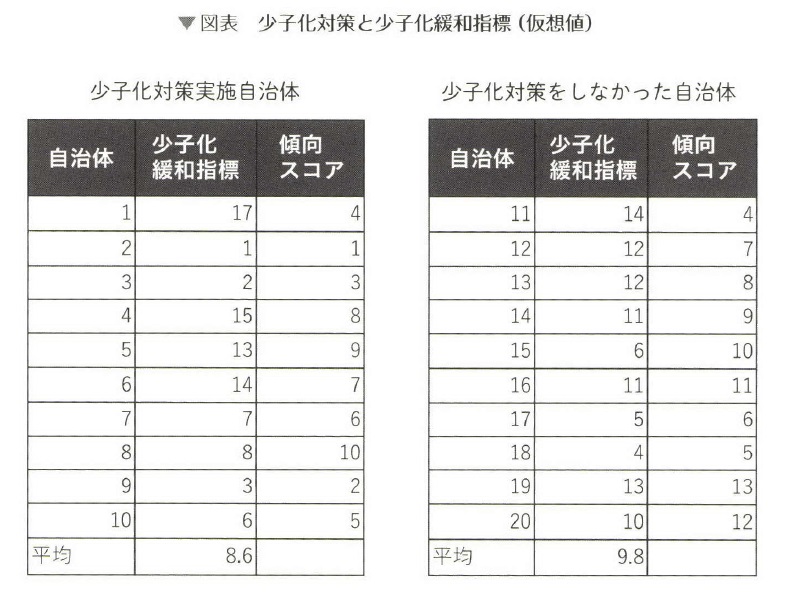
少子化緩和指標というのは、少しわかりにいですが、少子化が緩和されている度合いの高い自治体を表しているということです。
少子化対策を実施した自治体の少子化緩和指標の平均は8.6、少子化対策をしなかった自治体の少子化緩和指標の平均が9.8なので、これだけをみると、少子化対策をしなかった自治体の方が、少子化緩和効果が大きいと一見、考えられます。
しかし、条件が違う自治体どうしを比べてもあまり意味がありません。たとえば、東京都と沖縄県の合計特殊出生率を比べると、沖縄県の方が合計特殊出生率が高いですが、これは少子化対策の実施の有無というよりは人口や女子労働力率の影響の方が大きく、政策効果のみによる差ではないでしょう。
そこで、政策効果を比べるためには、傾向スコアが似た者同士で、比較することを考えます。
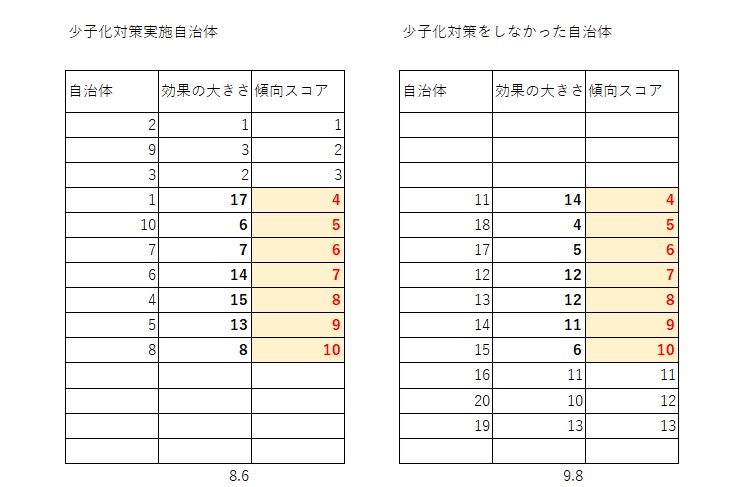
表を傾向スコアの順に並べ替え、同じ傾向スコアどうしの効果の大きさを比べます。
傾向スコアが４の場合は、自治体10（効果の大きさ17）と自治体11（効果の大きさ14）とを比べるということです。
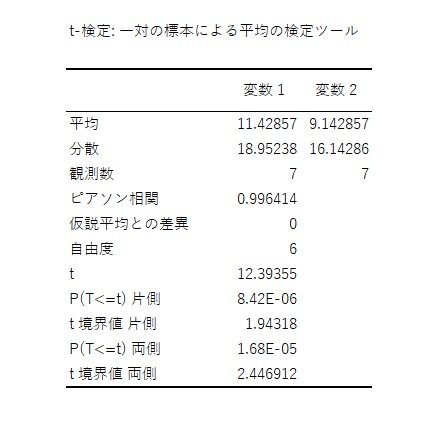
一対の標本による平均値の検定
傾向スコアが等しい同士のペアを1対の標本と考え、「一対の標本による平均値の検定」を行います。
t値は12.4、ｐ値は8.42E-06でほぼゼロとなり、「平均値の差が等しい」という帰無仮説は棄却されます。つまり、少子化対策には効果があることがわかるということです。
経済統計の使い方では、経済統計の入手法から分析法まで解説しています。
- 【Python】Pythonの基本操作
- 経済学Q＆A（試験編）
- 【経済統計】消費をみるために必要な月次指標ベスト３｜消費総合指数、商業動態統計、家計調査
- 経済統計チャットボット マホナ
- 経済金融指標の見方 Q&A２
