【統計学】区間推定｜信頼区間を提示して幅をもって示す

経済統計の使い方では、統計データの入手法から分析法まで解説しています。

統計学・計量経済学のまとめ 統計学に関するまとめのサイトです。 教科書 「回帰分析から学ぶ計量経済学－Excelで読み解く経済の仕組み」 回帰分...

区間推定とは

点推定は、ピンポイントで、〇〇である！と言い切るものですが、区間推定はもう少し自信がなく〇〇から××までの間と推定するものです。

しかし、統計学による推定なので、95％の信頼区間で、などある確率のもとで幅をもって推定します。

母分散が分かっている場合

最初に、分散が既知な場合です。たとえば、分散＝100、標準偏差＝10などが分かっている場合です。　

使うのは標準正規分布に関する以下の知識です。

標準正規分布をする確率変数Ｘが、95％の確率であてはまる範囲は、‐1.96≦X ≦1.96

標準化

推定しようと思う変数Xをまず標準化して、標準正規分布の世界に落とし込みます。

変数Xが標準正規分布（平均＝０，標準偏差＝１）になるように変換することを標準化といいます。

標準化すると確率分布（ｘの値が〇になるのは×％くらい）がわかるようになります。

$X$を変数　$\mu$を平均 $\sigma$を標準偏差とすると以下の式になります。

$Z={\displaystyle \frac{X-\mu }{\sigma }}$

標本平均の標準化

• 標本平均（$\overline{X}$ )の分布を考えます
• 母集団の平均を$\mu$とします
• 分散は既知で、$sigm{a}^2$とします
• $\overline{X}$を標準化したものは、標準正規分布に従います。標本平均の分散は${\displaystyle \frac{{\sigma }^2}{n}}$なので以下の式が成り立ちます。

$T={\displaystyle \frac{\overline{X}-\mu }{{\displaystyle \frac{\sigma }{\sqrt{n}}}}}$

区間推定の手順

標準正規分布になるように、標準化します。（標準正規分布なら、信頼区間がわかるため）

${\displaystyle \frac{\overline{X}-\mu }{{\displaystyle \frac{\sigma }{\sqrt{n}}}}}$ ($\overline{X}$:標本平均、$\mu$:母集団の平均、$\sigma$：母集団の標準偏差、$n$:サンプル数）

信頼区間95％の場合

$-1.96\le {\displaystyle \frac{\overline{X}-\mu }{{\displaystyle \frac{\sigma }{\sqrt{n}}}}} \le 1.96$

標本平均($\overline{X}$)と信頼区間の関係を式で表します。

$\mu －1.96{\displaystyle \frac{\sigma }{\sqrt{n}}}\le \overline{X}\le \mu +1.96{\displaystyle \frac{\sigma }{\sqrt{n}}}$

その式を母集団の平均に関する式に変形します。

$\overline{X}－1.96{\displaystyle \frac{\sigma }{\sqrt{n}}}\le \mu \le \overline{x}+1.96{\displaystyle \frac{\sigma }{\sqrt{n}}}$

母分散が未知の場合

• 分散が未知な場合、分散は不偏分散を使います。
• 平均も分散も標本から使うと、正規分布に従いません。
• t分布に従います。

標本平均の標準化

• 標本平均（$\overline{X}$)の分布を考えます
• 母集団の平均を $\mu$とします。
• 分散は不偏分散$U^2$を使います（使うしかありません）。
• $\overline{X}$を標準化したものは、自由度n-1のt分布に従います。

$T={\displaystyle \frac{\overline{X}-\mu }{{\displaystyle \frac{U}{\sqrt{n}}}}}$

ｔ分布

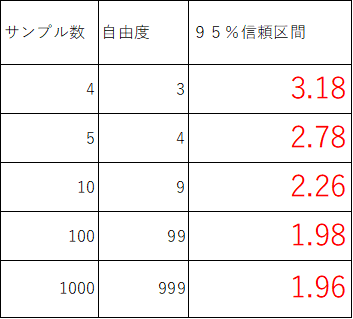
t分布は正規分布とよく似ています。ただ、95％の信頼区間はサンプル数によってかなり変わります。標本平均を標準化したものは、サンプル数がnの時、自由度n-1のt分布に従います。

標準正規分布の95％信頼区間は1.96です。サンプル数が1000個になれば、標準正規分布とほぼ同じ分布になります。

区間推定の手順

標準正規分布になるように、標準化します。（標準正規分布なら、信頼区間がわかるため）

${\displaystyle \frac{\overline{X}-\mu }{{\displaystyle \frac{\sigma }{\sqrt{n}}}}}$ (X ̅:標本平均、μ:母集団の平均、u：不偏分散から作った標準偏差、n:サンプル数＝10の場合）

•信頼区間95％の場合

$-2.26\le {\displaystyle \frac{\overline{X}-\mu }{{\displaystyle \frac{U}{\sqrt{n}}}}}$ ($\overline{X}\le 2.26$

•標本平均（X ̅)と信頼区間の関係を式で表す。

$\mu －2.26{\displaystyle \frac{U}{\sqrt{n}}}\le \overline{X}\le \mu +2.26{\displaystyle \frac{U}{\sqrt{n}}}$

•その式を母集団の平均に関する式に変形する。

$\overline{X}－2.26{\displaystyle \frac{U}{\sqrt{n}}}\le \mu \le \overline{X}+2.26{\displaystyle \frac{U}{\sqrt{n}}}$

• 【python】リスト君の大変身
• 【python】 クラスとインスタンス
• 【python】関数の作成
• AI関連の分析ツールの紹介ーー生成AIなど
• 【Python】Pythonの基本操作

検索

検索