母集団から標本を取り出して、母集団の平均（母平均）についての仮説を検定する場合です。この記事では、母集団の分散がわからない場合の方法を説明します。平均がわからないのに、母集団の分散がわかるのは不自然ですよね。こちらの方が普通の検定の方法です。
母集団の分散がわかっている場合はこちらの記事を参考にして下さい。
経済統計の使い方では、統計データの入手法から分析法まで解説しています。
t分布を使います
母集団の分散がわからない場合は、標本から分散を計算します（不偏分散）。
不偏分散を使った場合は、標本平均は標準正規分布ではなく、ｔ分布に従います。
ｔ分布とは
ｔ分布は、標準正規分布と似た分布で、山型をしています。
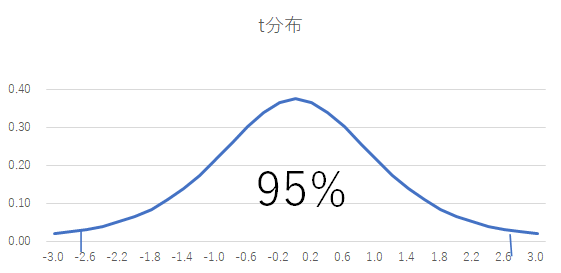
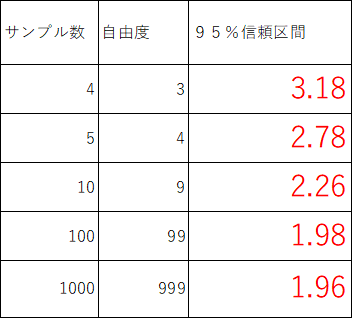
ただ、サンプル数によって、山の形がかなり変わります。95％の信頼区間を見ると、サンプル数がnの時、自由度n-1のt分布に従います。サンプル数が４では3.18、1000では1.96となります。サンプル数が多い場合は、標準正規分布とほぼ同じになります。
ビールの容量の検定
あるビールメーカーは平均内容量350㎤と主張しているとします。しかし、それより少ないような気がしたので、調べることにしました。
試しに100本について平均をとると、348.0 ㎤でした。
標本から計算した不偏分散は 8２ $(㎤)^2$ でした 。
以下の仮説を有意水準５％水準で検定します。
- 帰無仮説(H0)：350 ㎤で変化がない
- 対立仮説(H1)：350 ㎤より減った
検定方法は以下の手順に従います。
- 有意水準（偶然では起こりえないほど珍しい確率）を決めます。今回は5％以下です。
- 帰無仮説（母集団平均は350㎤）からt分布を使って棄却域を決めます。
- 標本平均を調べます。
- 標本平均が棄却域に入れば帰無仮説が棄却されます。
- 対立仮説が正しいということになります。
t分布での棄却域を計算
帰無仮説を前提として、ｔ分布の５％に入る部分を考えます。今回は平均が350㎤で変らないことを前提に、偶然では起こりえないほど珍しい確率になるのはどこなのかを考えます。
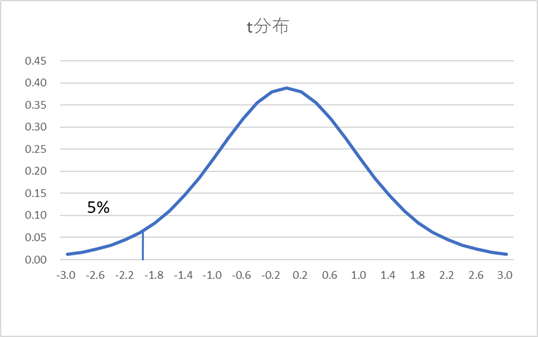
まずｔ分布の棄却域をエクセルで求めます。以下の関数を使えば計算できます。自由度はサンプル数-１です。
T.INV(有意水準,自由度)
今回の課題では、片側検定で有意水準5％、サンプル数100なので、T.INV(0.05,100-1)=-1.66となります。
棄却域の計算
棄却域は以下の式で計算できます。ただし、$\mu$は母集団の平均、$T$はt分布の棄却域、$U$は不偏分散、$n$はサンプル数です。
$ \mu+T ×\dfrac{U}{\sqrt{n}} $
帰無仮説を前提にすると母集団は350、不偏分散は$8^2$、サンプル数は100なので以下の計算になります。
$350-1.66×\dfrac{8^2}{\sqrt{100}}=348.7$
棄却域は348.7未満だということがわかります。
標本を取り出した結果は、348㎤で棄却域は348.7㎤未満なので棄却域に入っており、帰無仮説を棄却できます。
つまり、ビールは350㎤より小さいことが統計的に明らかになったことがわかります（あくまでフィクションですが…）。
まとめ
- 分散が未知の場合の母平均に関する検定の方法を説明しました。
- ｔ分布を使います。
- エクセルから、t分布の棄却域を調べます。
- 平均と棄却域と不偏分散から、標本平均に対応する棄却域を調べます。
- 棄却域に入っていれば帰無仮説を棄却します。
- 【時系列分析】課題３ ドリフト付きランダムウォーク
- 【時系列分析】課題２ グレンジャーの因果関係
- 【時系列分析】課題１ 為替レートの予測
- 「回帰分析から学ぶ計量経済学」を使ったセミナーを行います(2024年３月８日）
- 正誤表 回帰分析から学ぶ計量経済学
