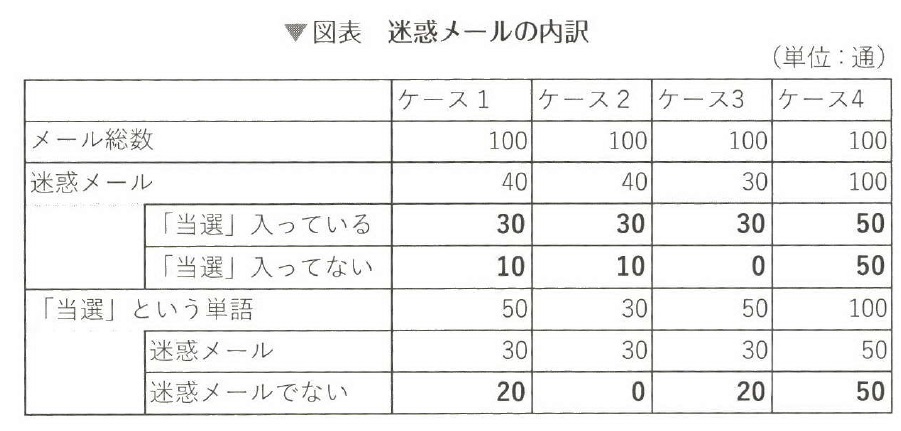
ナイーブベイズはベイズの定理を使います。メールの中に「当選」という言葉が入っていたとき、そのメールが迷惑メールである確率を以下の4ケースで求めてみ
て下さい。
事前確率:全メールのうちで迷惑メールの確率
尤度:迷惑メールであるとき、「当選」という言葉が入っていることの妥当性
全確率:全メールのうちで「当選」という言葉が入っている確率
事後確率:「当選」という言葉が入っていたとき、そのメールが迷惑メールである確率
（正誤表）ケース４の最下段は50→０としてください。
メールの中に「当選」という言葉が入っていた時、そのメールが迷惑メールである確率とは、事後確率の事です。
事後確率は以下の式で求めることができます。
$事後確率＝\dfrac{尤度×事前確率}{全確率}$
ケース１からケース４まで計算すればよいわけですが、それぞれのケースがどのようなケースかを開設します。
ケース1：これは一般的なケースです。事前確率は40％、尤度は75％、全確率は50％で事後確率は60％になります。
ケース2：ケース２は、「当選」という単語が入っていた場合は、必ず迷惑メールである場合で、この場合は、「当選」という単語が入っていれば迷惑メールである確率は100％になります。
ケース３：迷惑メールには必ず「当選」という言葉が入っている場合です。これは尤度が100％であることを示します。当選という言葉が入ってるメールのうち迷惑メールである確率は50通中30通なので、確率は60％です。
ケース4：すべてのメールが迷惑メールの場合です。事前確率が100％であることを示します。「当選」という言葉が入っていても入っていなくても迷惑メールなわけですから確率は100％です。
結果をまとめると以下になります。
| ケース１ | ケース２ | ケース３ | ケース４ | |
| 事後確率 | 60％ | 100％ | 60％ | 100％ |
経済統計の使い方では、経済統計の入手法から分析法まで解説しています。
- 分析ツールの紹介
- 【Python】Pythonの基本操作
- 経済学Q＆A（試験編）
- 【経済統計】消費をみるために必要な月次指標ベスト３｜消費総合指数、商業動態統計、家計調査
- 経済統計チャットボット マホナ
