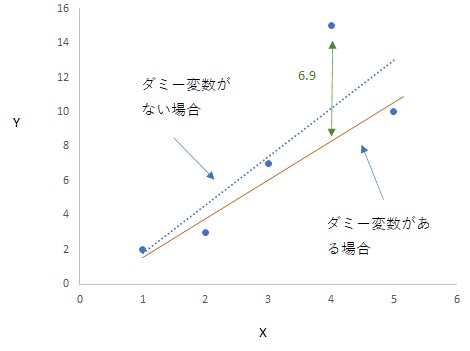
機械学習では特定のデータだけに当てはまりがよくなり、汎用性がなくなってしまう過学習という問題があります。
それを回避するために考えられたのが正則化回帰です。LASSOとリッジ回帰とが代表的です。
経済統計の使い方では、統計データの入手法から分析法まで解説しています。

複雑さを回避する正則化回帰
回帰分析は機械学習でも使われています。最小二乗法の延長線上にある分析として正則化回帰があります。
機械学習の問題点として、過学習があります。特定のデータについて当てはまりのよいモデルを作ると、そのデータについては当てはまりが良くても、他のデータについては予測がうまくできないという問題です。
その解決法として、モデルの複雑さを表す指標を作り、複雑さが大きくならないようにする方法が考えられ、正則化回帰と呼ばれています。
通常の最小二乗法では、残差の二乗和を最小にしますが、そこに複雑さを表す正則化項を付けます。
残差の二乗和に正則化項を加えた以下の目的関数を最小にします。
$目的関数=損失関数(残差の二乗和)\text{+} \color{red} 正則化項(複雑さ)\color{black} $
L2正則化(リッジ回帰)
説明変数が2つの場合を考えると、以下の目的関数を最小化するのがリッジ回帰です。
$ \Sigma_{i=1}^n ( y_i- (\alpha- \beta_1 x_i – \beta_2 x_i)) ^2 + \lambda (\beta_1^2+\beta_2^2) $
βに制約がある中で、残差二乗和の最小化するということです。βが動ける領域の中で、残差二乗和が最小になる場所を探すことになります。2変数で考えた場合、リッジ回帰では制約する領域が円になるので、βがゼロになることはありませんが、βの大きさに制約がかかるので、係数が小さくなります。
L1正則化(LASSO)
説明変数が2つの場合を考えると、以下の目的関数を最小化するのがLASSO(least absolute shrinkage and selection operator)です。
$ \Sigma_{i=1}^n ( y_i- (\alpha- \beta_1 x_i – \beta_2 x_i)) ^2 + \lambda (|\beta_1|+|\beta_2|) $
βに制約がある中で、残差二乗和の最小化するということです。βが動ける領域の中で、残差二乗和が最小になる場所を探すことになります。2変数で考えた場合、LASSOの場合は制約領域が正方形になるので、最小値が軸上になります。一つの変数はゼロになるということで、説明変数を減らす効果があります。
計算例
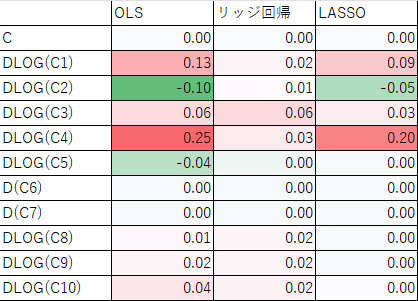
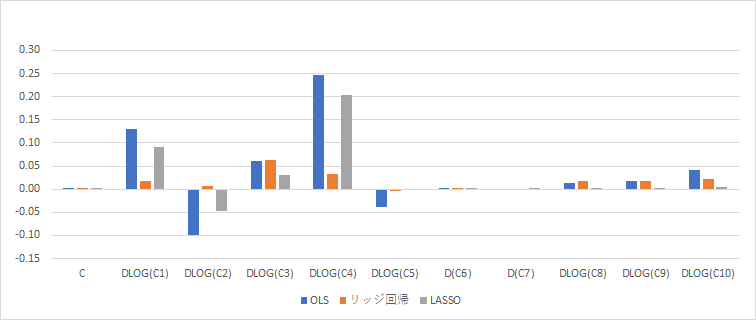
3つの推計による推計結果を比べたものです。実質GDP(対数階差)を被説明変数、説明変数に定数項と、景気動向指数一致指数の構成項目(C1からC10まで)の対数階差または階差をとったものです。表とグラフで示しています。
最も左の列が通常の最小二乗法(OLS)です。左から2番目がリッジ回帰で、係数が全体的に小さくなっていることがわかります。最も右がLASSOです。LASSOでは係数がゼロになっているものが増えていることがわかります。
まとめ
- 回帰分析の応用である正則化回帰を解説しました
- 過学習を防ぐため、複雑さも考慮して推定します
- リッジ回帰では係数の大きさが抑えられます
- LASSOでは係数がゼロの説明変数が増えます