回帰分析をするにあたって、覚えておくべきポイントの一つに対数があります。
対数線形で推定すると、推定した係数が弾力性を表し、推定式の解釈が容易になります。
また、対数階差は前期比伸び率の近似値で、推計しようとする系列が非定常系列の場合、対数階差で推計する場合が多いです。
経済統計の使い方では、統計データの入手法から分析法まで解説しています。

対数とは
対数は、 $Y=X^a$ の関係がある時、$a$のことを指します。対数の底はe(ネイピア数)を使うことが多く自然対数と呼ばれます。 $Y= e^a$の$a$のことです。
対数で表すと、さまざまな変数の大きさを比較可能な形で圧縮してくれます。
$ \log1=0 $
$ \log e=1 $
$ \log 1000=6.9 $
$ \log 1億=18.4 $
1はゼロで、1000が6.9、1億でも18.4になります。大きな数字が圧縮されることで、データが扱いやすくなります。
対数線形
対数線形は被説明変数と説明変数の両方を対数にして推定するものです。
式の形は以下になります。
$ \log (Y)=a+b \log (X) $
係数は弾力性(弾性値)を表します。弾力性は、$X$が1%増えた時に、$Y$がb%増えることを表します。
回帰分析でよく使う手法で、非常に便利なものなので覚えておきましょう。
対数線形にすると、被説明変数や説明変数の単位に関係なく係数は弾力性を表すので、非常に便利です。YやXが100万円単位で表されていても、10億円単位で表されていても、あるいはYとXで単位が違っても、同じ弾力性が計算できます。
なぜ弾力性になるのかは以下の式の変形で理解できると思います。
$ \log(Y)=a+b\log(X) $
$ \dfrac{d\log(Y)}{dX}= b\dfrac{d\log(X)}{dX} $
$ \dfrac{d\log(Y)}{dY}×\dfrac{dY}{dX}= b\dfrac{1}{X} $
$ \dfrac{1}{Y}×\dfrac{dY}{dX}= b\dfrac{1}{X} $
$ b=\dfrac{dY/Y}{dX/X} $
対数階差
対数階差もよく使われます。もとの系列の対数をとり、その前期との差を表します。近似的には対数階差=前期比伸び率です。
非定常系列を定常系列にするために、階差をとることが多いですが、対数階差をとってもいいです。
非定常系列についてはこちらを参照してください。
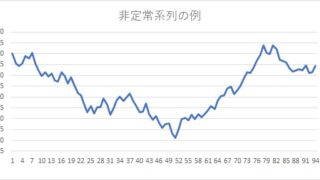
対数階差が前期比伸び率に近似できるというのは以下の式で表されます。
$ \Delta \log y_t \approx \dfrac{y_t-y_{t-1}}{y_{t-1}} $
これが成り立つことを説明します。yが指数的に増える場合、前期比伸び率をg、初期値をaとして以下の式で表されます。
$ y_t=a e^{gt} $
両辺の対数をとります。
$ \log y_t = \log a +gt $
これの階差をとります。
$ \log y_t – \log y_{t-1} = gt-g(t-1)=g$
対数階差が前期比伸び率に近似できることを示しています。