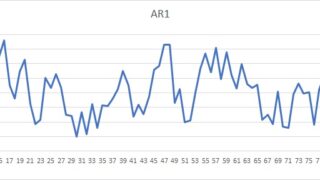
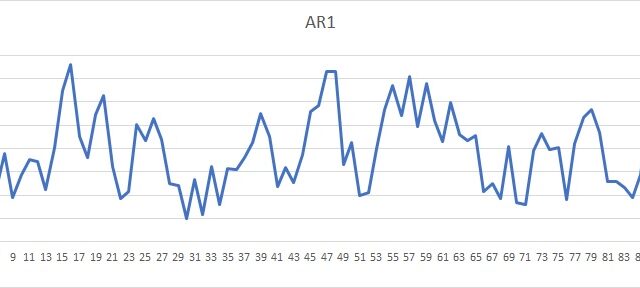
最小二乗法で推計するときに気を付けないといけないことの一つが、推定に使う系列が「非定常系列」かどうかです。非定常系列の場合はそのまま推定するのは適当ではなく、階差をとって推計することが必要です。
経済統計の使い方では、経済統計の入手法から分析法まで解説しています。

非定常系列とは
非定常系列とは、定常系列ではない、ということです。定常系列とは、落ち着いた系列というイメージです。同じ程度の幅を行ったり来たりするイメージです。
非定常系列とは落ち着きがない系列で、上がっていったと思ったら急に下がったり、そうかと思えばその後はずっと上がり続けたり…などのイメージです。
定常系列の厳密な定義は以下の3つです。ARIMAモデルは定常系列です。これを満たさないものが非定常系列となります。
- 平均が一定
- 分散が一定
- 自己相関が一定
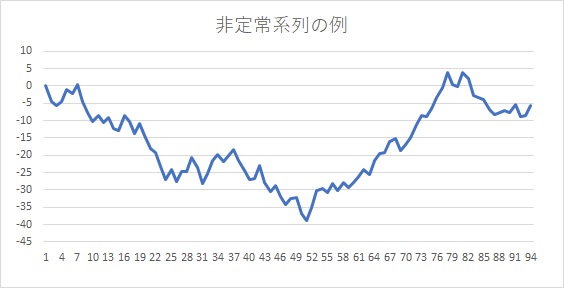
なぜ重要か
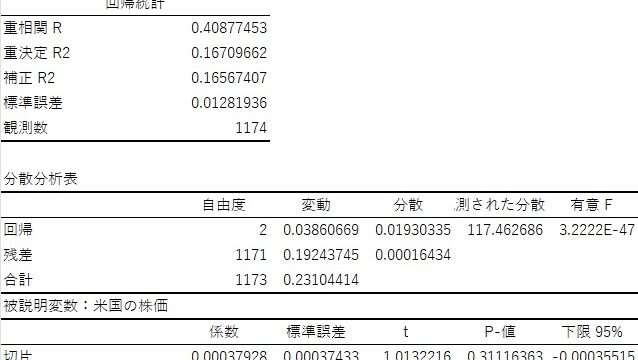
非定常系列どうしで回帰分析をすると、決定係数やt値に関して高い値が得られることがあります。しかし、実際には相関関係や因果関係がまったくない場合があります。見せかけの回帰と呼ばれる現象で、不適切な推計の一つになります。
定常系列にするには
非定常系列を定常系列にするには階差(前期との差)をとった系列にします。たいていの系列は階差をとることで定常系列になります。
階差を1回とって定常になる系列をI(1)と呼びます。階差をとる回数がカッコの中にはいります。階差を2回とって定常になる系列はI(2)です。
階差をとらない(階差を0回とる)で定常な系列はI(0)と呼ばれます。I(0)とは定常系列のことです。
単位根とは
非定常系列は単位根を持つ系列とも呼ばれます。方程式の解(根)が1ということで、英語のunit rootを訳したものです。
ここでいう根とは、自己回帰モデルの係数を表していて、AR(1)の場合だと、1期前の係数aが1であるということです。
- ARモデル
$ Y_t=aY_{t-1} +e_t $
- 単位根系列
$ Y_t=Y_{t-1} +e_t$
根を求める方程式について詳しく説明すると、定常性の条件を決定する固有方程式のことです。
ランダムウオークとは
単位根を持つ系列はランダムウオークします。ランダムウオークとは酔歩過程とも呼ばれ、酔っ払いが千鳥足で歩いているような系列の動きを指します。
単位根系列の式を見ていただければわかるように、次の系列を予測するために必要なのは1期前の系列と偶然の誤差である$e_t$のみです。このため、予測が非常に難しいです。
非定常系列=I(1)=単位根系列=ランダムウオーク
厳密には、非定常系列は定常系列でない系列すべてなので最も広い定義です。
I(1)とは、1階階差をとると定常系列になるものですが、経済系列のほとんどがこれにあたります。I(2)の場合もありますが、I(1)が非定常系列、I(0)が定常系列と考えてそれほど困りません。
I(1)の代表的なものがランダムウオーク系列になります。
単位根検定
単位根があるかどうかの検定を単位根検定と呼びます。
単位根検定には、通常ディッキーフラーテストを使います。帰無仮説が「単位根を持つ」なので、仮説を棄却できない場合は単位根系列である可能性があるということになります。
詳しくは「実戦計量経済学入門」を参照してください。