物価指数は、さまざまな品目の価格を総合して表すものです。
消費者物価指数や企業物価指数が代表的なものです。指数の計算にはラスパイレス式が使われます。
一方、GDPデフレーターはパーシェ式です。
ラスパイレス指数には上方バイアスが、パーシェ指数には下方バイアスがあるので、最近は連鎖式が使われます。
経済統計の使い方では、統計データの入手法から分析法まで解説しています。


物価指数とは
物価指数は、さまざまな品目の価格を総合して表すものです。リンゴやミカン、イチゴといった違うものの物価を組み合わせることになります。
基本的な考え方は、消費金額が多いものには大きなウエート、小さなものには小さなウエートにして品目別の価格指数を加重平均するというものです。
また、毎月発表される場合は、簡単に調査できる方法が望ましいです。このため、消費者物価指数や企業物価指数は、比較時点では価格だけ調べればよいラスパイレス指数を使っています。
ラスパイレス指数
ラスパイレス指数は、価格を$P$、数量を$Q$、基準時点を0、比較時点をtとすると以下の式となります。
$ \dfrac { \sum {P_t Q_0 } }{ \sum {P_0 Q_0 } } $
価格については、基準時点と比較時点の両方が必要ですが、数量については基準時点しか使っていません。比較時点に数量を調べなくてもよいので、高頻度で調査する物価指数に便利です。
また、ラスパイレス指数を変形すると、以下の式になります。1財からn財までを考えます。$w_{n0}$は基準年次での消費金額のウエートで、$ \frac{P_{n0}Q_{n0}}{\sum{p_0 Q_0} } $です。
$ \frac{P_{1t}}{P_{10}} ×w_{10} + \frac{P_{2t}}{P_{20}} ×w_{20} +\frac{P_{3t}}{P_{30}} ×w_{30}+ … \frac{P_{nt}}{P_{n0}} ×w_{n0} $
つまり、個別の指数を基準年の消費金額をウエートとして加重平均しているということになります。
パーシェ指数
パーシェ式は、以下の式です。
$ \dfrac { \sum {P_t Q_t } }{ \sum {P_0 Q_t } } $
ラスパイレス式とは反対に、基準年の数量は使わず、比較年の数量のみを使っています。
GDPデフレータはパーシェ式です。
なぜGDPはパーシェ式なのか
消費者物価指数や、企業物価指数など、物価指数のほとんどがラスパイレス指数なのに、なぜ、GDPデフレーターはパーシェ指数なのでしょうか?
それは、物価指数作成法の問題ではなく、名目GDPや実質GDPの定義に関係があります。名目GDPは金額指数で、実質GDPは基準年の価格で表した数量指数という定義です。
名目GDPは、以下の式になります。比較時点での価格と数量を掛け合わせたものです。
$ \sum{ P_t Q_t } $
実質GDPは、以下の式になります。比較時点での数量を、基準時点での価格で評価したものです。
$ \sum{ P_0 Q_t } $
GDPデフレーターは名目GDPを実質GDPで割ったものなので、以下の式です。
$ \dfrac { \sum {P_t Q_t } }{ \sum {P_0 Q_t } } $
これは、分母、分子ともに比較年の数量を使っており、パーシェ指数になります。
名目GDPは、GDPの構成項目について名目値を足し上げて作成し、実質GDPはGDPの構成項について実質値で足し上げて作ります。GDPデフレーターは、名目GDPを実質GDPで割ってつくります。直接GDPデフレーターを推計するわけではないので、インプリシット(暗黙の)デフレーターと呼ばれます。
バイアスのない指数にフィッシャー指数があり、「理想算式」と呼ばれます。
$ \sqrt{ ラスパイレス指数 × パーシェ指数 } $
これをGDPデフレーターに使うと、実質GDPは以下で表されますが、「基準年で作った数量指数」という解釈はできなくなります。
$ \dfrac { \sum{ P_t Q_t } } { \sqrt{ \frac { \sum {P_t Q_0 } }{ \sum {P_0 Q_0 } } \frac { \sum {P_t Q_t } }{ \sum {P_0 Q_t } } } } $
ラスパイレス指数の上方バイアス
ラスパイレス指数は基準時点の消費金額ウエートで加重平均しています。比較時点の数量の情報は反映されていません。
基準時点から比較時点にかけて価格が上がった商品は、代替効果で購入数量が減るはずなので、通常比較時点でのウエートは、基準時点より低くなるはずです。
反対に、基準時点から比較時点にかけて価格が下がった商品は、購入数量が増えるはずです。
このため、ラスパイレス指数は、実態よりも高めに計算されることになります。
反対に、パーシェ指数は、実態よりも低めに計算されます。ラスパイレス指数の消費者物価指数の前年同期比は、パーシェ指数の民間最終消費デフレーターよりも高めに計算されています。
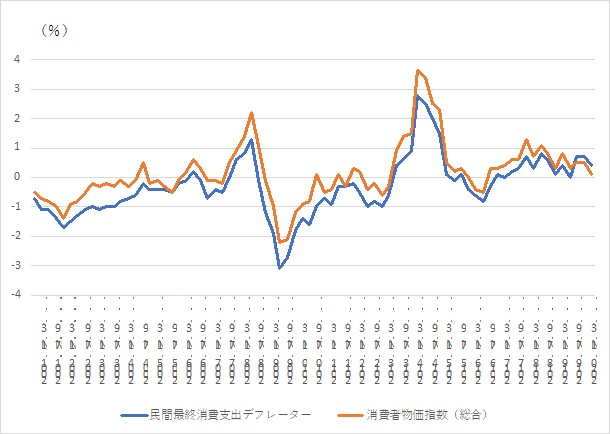
固定基準年式と連鎖方式
物価指数には従来固定基準年方式で計算されてきました。しかし、ラスパイレス指数やパーシェ指数の場合は、上記のようなバイアスが発生します。
この問題を解決するには、基準年を固定せず、常に前年を基準とウエートを計算する方法が考えられ、連鎖方式と呼ばれます。この方法だと、ウエートを固定することによる弊害がなくなります。















