主成分分析は、多数の変数を一つにまとめる方法です。たとえば、国語、数学などの点数を一つにまとめて、総合的な得点の指標を作ることができます。さまざまな変数の共通の動きを主成分として取りだすということです。
式で書くと以下が基本です。
$z=w_1x_1+w_2x_2 $
変数$x_1$と$x_2$から$z$という新たな変数(主成分)を作っています。
エクセルでは計算できませんが、無料ソフトgretlを使えば計算できます。
経済統計の使い方では、統計データの入手法から分析法まで解説しています。


学校の成績の例
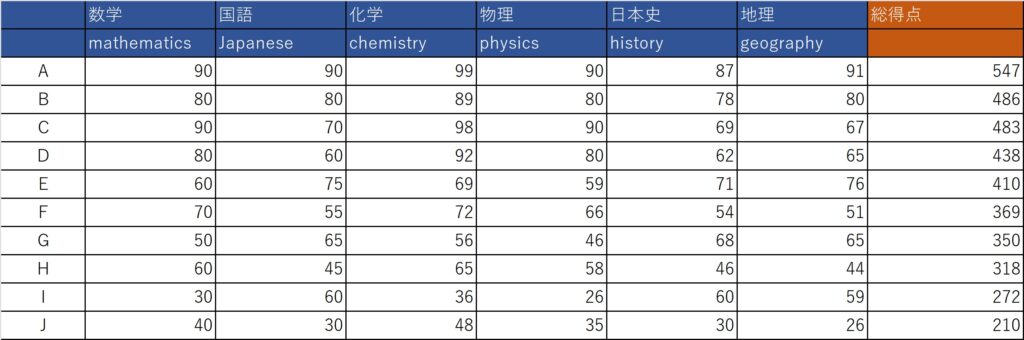
主成分分析の例として、学生10人の国語、数学、化学、物理、歴史、地理の点数を主成分分析に適用する場合を紹介しましょう。データは以下の通りです。AからJまで総得点の高い順に並んでいます。
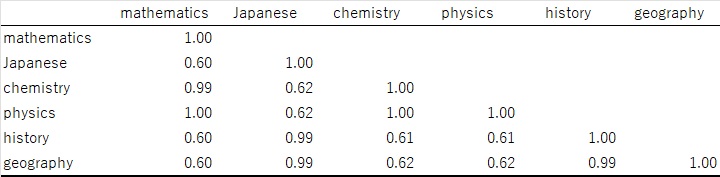
相関係数行列は以下の通りです。数学と化学、物理の相関が高く、国語と日本史、地理の相関が高いデータになっています。
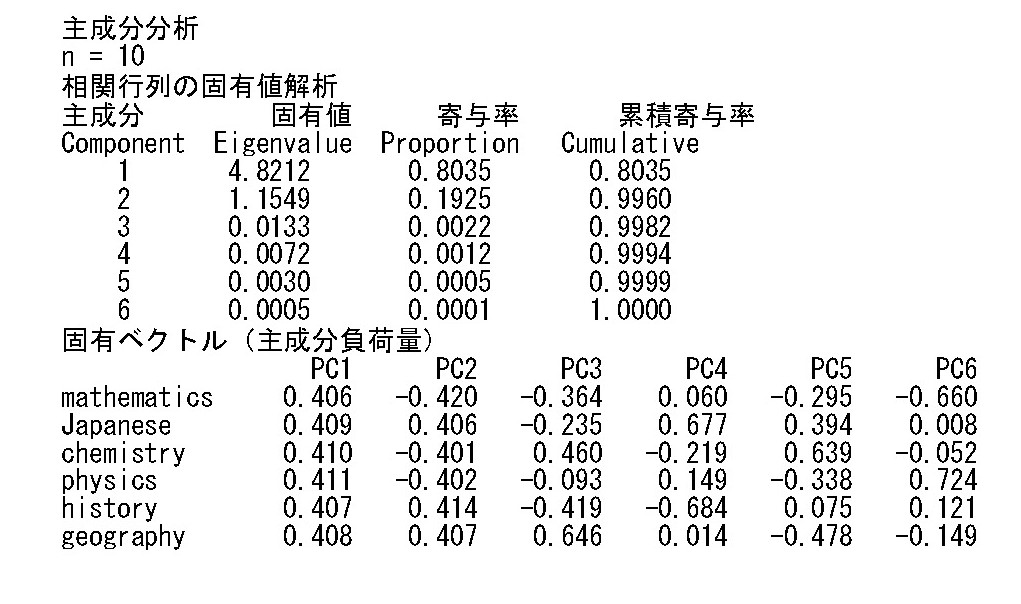
主成分分析の結果
gretlで分析した結果は以下のように出力されます。一つ目の表は相関行列の固有値解析です。主成分は6個あり、それぞれ、固有値、寄与率、累積寄与率が計算されます。
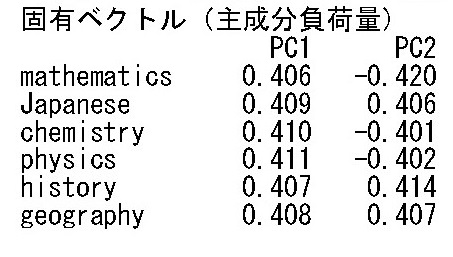
固有ベクトル(主成分負荷量)の表では、PC1が第一主成分、PC2が第2主成分を表します。科目ごとに主成分負荷量が計算されています。
主成分は、変数が6個であれば、6個作成されます。しかし、すべての主成分が重要というわけではありません。
固有値は情報の含有量を表す―大きいほど重要な主成分
第1主成分から第6主成分には、それぞれ固有値が対応しています。固有値の大きさは、各主成分が元の情報をどの程度反映しているかを表しています。相関行列を使った場合は、変数は標準化されており、分散は1です。固有値が1を超えているということは、元の変数よりも情報量が多いということで意味があるといえます。この分析では、第1主成分と第2主成分に意味がありそうです。
固有ベクトルは、各変数の主成分への影響力を表す
固有ベクトルは主成分を計算する際のウエートです。各変数(上の例では各科目)の役割をみるのに有効です。ただ、固有ベクトルは、二乗和が1という制約をかけたもので、変数が増えると値が小さくなりますので、因子負荷量(主成分負荷量)をみるのが適当です。
因子負荷量は、固有ベクトルと比例して動きますが、相関係数を表すので、変数の数に影響されず、常にマイナス1から1の間の数値で、特徴を示します。
また、因子負荷量と固有ベクトルは以下の関係があります。
$ 因子負荷量=\sqrt{固有値} × 固有ベクトル$
各主成分の固有値は同じですから、因子負荷量と固有ベクトルは定数倍に関係にあることがわかります。
上の表から第1主成分と第2主成分の固有ベクトルを抜き出しのが下の表です。
第1主成分の固有ベクトルをみると、それぞれの科目にかかる係数はすべて正で、それぞれおよそ0.4になっています。平均を計算するのとあまり変わらない結果で、総合的な成績を表しているといえます。
第2主成分の固有ベクトルの結果をみると、国語(0.406)、歴史(0.414)、地理(0.407)の係数は正である一方、数学(-0.420)、化学(-0.401)、物理(-0.402)の係数は負となっています。この主成分が表すのは、文科系の成績を表しているといえます。
主成分得点の結果
次に、以下の式を使って、学生それぞれの第1主成分を計算してみましょう。相関行列を使って主成分分析をした場合は、得点($X$)ではなく、得点を基準化($\dfrac{X-平均}{標準偏差}$)したものを代入します。
$ 第1主成分=0.406×数学\text{+}0.409×国語\text{+}0.410×化学\text{+}0.411×物理\text{+}0.407×歴史\text{+}0.408×地理$
第2主成分は以下の式で計算できます。
$ 第2主成分=\text{-}0.420×数学\text{+}0.406×国語\text{-}0.401×化学\text{-}0.402×物理\text{+}0.414×歴史\text{+}0.407×地理$
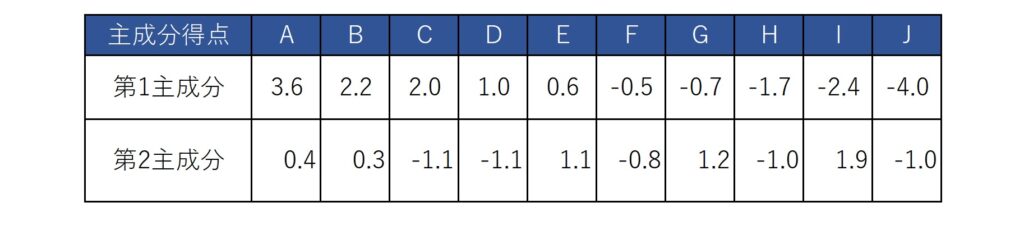
結果は以下になります。第1主成分は得点の多い順になりますが、第2主成分は相対的に文科系の科目ができる学生ほど高くなります。
2変数による説明
主成分分析の考え方について、2つの変数を使った場合について説明します。主成分分析は、2つの変数$x_1$,$x_2$の特徴を合わせ持つ変数$z$として作成します。
$$ z=a_1x_1+a_2x_2 $$
新たに作る変数$z$は、様々な値の中で最も分散の大きい変数とします。$z$の分散が大きいということは、個々の数値の散らばりが大きいということで、特徴をよりはっきりと表すことになるためです。最大になる組み合わせはいくつも考えられるため、$a_1^2+a_2^2=1$という制約を置きます。
分散の最大化を計算していくと、分散共分散行列について、固有値と固有ベクトルを求めることと同じことになります。新たに作成した系列の分散が固有値を表します。第一主成分は、最も大きい固有値とそれに対応する固有ベクトルを使って作成します。固有ベクトル(上式の$a_1$,$a_2$)をウエートにして新たな変数を作成します。
地域統計では
例えば、静岡県のふじのくに少子化突破戦略では、昼夜間人口比率、正規従業員数割合、就業者に占める若者の割合、完全失業率、市町民所得を一つの変数にまとめて「地域の働く力」というデータを作っています。
多くの変数がある場合は、第1主成分とは異なる特徴を持った第2主成分、第3主成分などを求めることができます。
主成分をする際は、1つにまとめても違和感のないデータを用いることが重要です。「地域の働く力」の指標を作るには、地域の働く力に関係がある指標のみを選択する必要があります。関係ない変数を入れてしまうと、何を表している指標かがわからなくなります。
固有値と主成分分析の関係
主成分分析のデータを解釈する場合、固有値分析の言葉が使われるので、その関係を説明します。行列をAとするとAの固有値と固有ベクトルには以下の関係があります。
$ Ax=λx $
主成分分析は合成変数$z=a_1x_1+a_2x_2+ \cdots +a_px_p $の式の分散を最大化させるということです。分散は多少複雑な計算の後、以下のように書けます。$v_{11}$は$x_1$の分散、$v_{12}$は$x_1$と$x_2$の共分散です。
$Var(z) = \begin{bmatrix} a_1, & a_2 & \cdots & a_p \end{bmatrix}\begin{bmatrix} v_{11} & v_{12} & \cdots & v_{1p} \\ v_{21} &v_{22} & \cdots & v_{2p} \\ \vdots & \vdots & \vdots & \vdots \\ v_{p1} & v_{p2} & \cdots &v_{pp} \end{bmatrix} \begin{bmatrix} a_1 \\ a_2 \\ \vdots \\ a_p \end{bmatrix} $
この式の分散を最大化をするということは、ラグランジュ乗数法で偏微分をゼロと置くことで求められます。この1階の条件をまとめると、以下の式となり、分散共分散行列の固有値を求めることと等しくなります。
$ \begin{bmatrix} v_{11} & v_{12} & \cdots & v_{1p} \\ v_{21} &v_{22} & \cdots & v_{2p} \\ \vdots & \vdots & \vdots & \vdots \\ v_{p1} & v_{p2} & \cdots &v_{pp} \end{bmatrix} \begin{bmatrix} a_1 \\ a_2 \\ \vdots \\ a_p \end{bmatrix} = λ\begin{bmatrix} a_1 \\ a_2 \\ \vdots \\ a_p \end{bmatrix} $
また、固有値と分散は等しくなります。
$Var(z)=λ$
以下をまとめると、次の表になります。
| 主成分分析 | 固有値分析 |
| 各主成分の分散 | 固有値 |
| 主成分負荷量 | 固有ベクトル |
| 分散共分散行列 | 行列 |