最小二乗法が正しい結果を出すための仮定に、「誤差項に系列相関がない」があります。系列相関とは、過去の自分自身の値との相関のことですが、多くの場合系列相関が除去できていない場合が多いです。
対応法として、コクラン・オーカット法が考案されています。明示的に系列相関を仮定することで、系列相関のない誤差を使った推計ができるという方法です。
この方法をエクセルを使ってやってみます。
経済統計の使い方では、統計データの入手法から分析法まで解説しています。


考え方
通常の最小二乗法は以下の式を推計します。
$ Y_t= \alpha + \beta X_t + u_t $
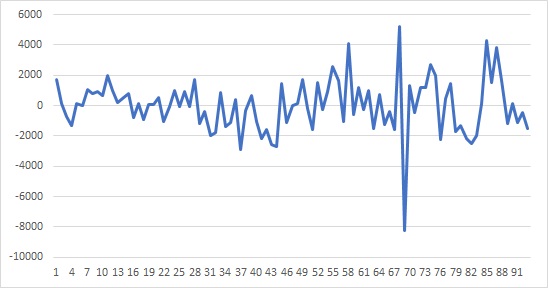
今回使ったデータの誤差$u_t$のグラフは以下のようになります。ランダムな動きとは違って、プラスの値の時はプラスの値が続き、マイナスの値の時はマイナスの値が続いています。誤差に系列相関がある例です。
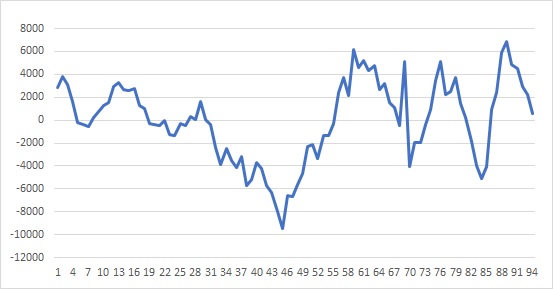
系列相関があるかどうかの検証法などは以下の記事を参考にしてください。
系列相関への対応として、コクラン・オーカット法があります。誤差に明示的に系列相関を想定し、以下の式を作ります。
$ u_t=\rho u_{t-1}+ \epsilon_t $
上記の基本式と、1期前の式に $\rho$ をかけた式を作ると、以下の式です。
$ Y_t= \alpha + \beta X_t + u_t $
$ \rho Y_{t-1}= \rho (\alpha + \beta X_{t-1} + u_{t-1}) $
辺々を引くと以下の式となります。それぞれの変数から1期前の変数×$\rho$ を引いたものになります。
$ Y_t- \rho Y_{t-1} =( \alpha-\rho \alpha) + \beta( X_t – \rho X_{t-1}) + (u_t – \rho u_{t-1}) $
上記の式を簡明に描くと以下のようになります。
$ Y’_t= \alpha’ + \beta’ X’_t + \epsilon_t $
ただし、それぞれの変数は以下を表します。
$ Y’_t=Y_t- \rho Y_{t-1} $
$ X’_t=X_t- \rho X_{t-1} $
$ \epsilon_t=u_t- \rho u_{t-1} $
$ \alpha’ = \alpha- \rho \alpha $
新たに作った式の誤差$ \epsilon_t $は系列相関が除去されていますので、最小二乗法で正しく推計できます。
実際の推定
実際には、$ \rho $ が判明してないので、まず、 $ \rho $ を推定する必要があります。以下の3段階で行います。
通常の最小二乗法を計算し、残差を計算する。
$ Y_t= \alpha + \beta X_t + u_t $
この回帰分析で$u_t$が得られます。
残差の自己相関係数を計算する
$ u_t=\rho u_{t-1}+ \epsilon_t $
$u_t$を$u_{t-1}$に回帰します。この回帰分析で$\rho$が得られます。
自己相関係数を使って、最小二乗法で計算する。
$ Y’_t= \alpha’ + \beta’ X’_t + \epsilon_t $
この回帰分析で、精度の高い回帰係数が得られます。$ \alpha $ は、$ \alpha’/(1 -\rho) $で得られます。
エクセルでの操作
通常の最小二乗法を計算し、残差を計算する
エクセルでは分析ツールの回帰分析を使います。エクセルによる通常の回帰分析の方法は、エクセル 回帰分析ーデータ範囲を設定するだけをご覧ください。

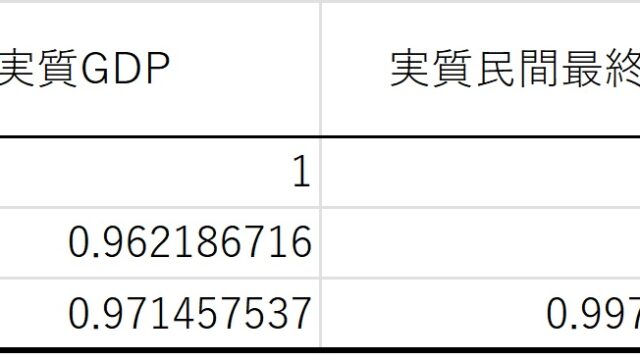
今回は、山澤成康「実戦計量経済学入門」の実質GDPと実質民間最終消費のデータを使いました。データは第5章5.63にあります。
今回は推定するだけでなく、残差のデータを入手する必要があるので、出力オプションの残差にチェックを入れます。
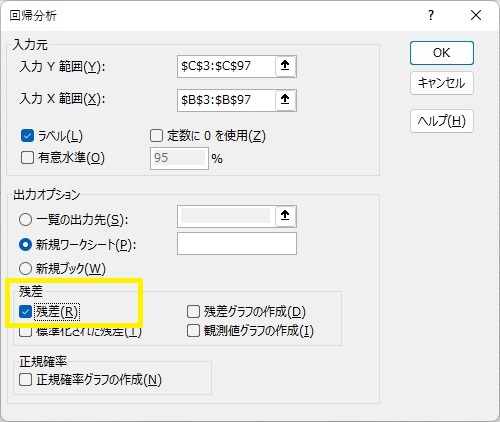
推定結果は以下のようになります。この結果の下に、残差のデータが並んでいます。
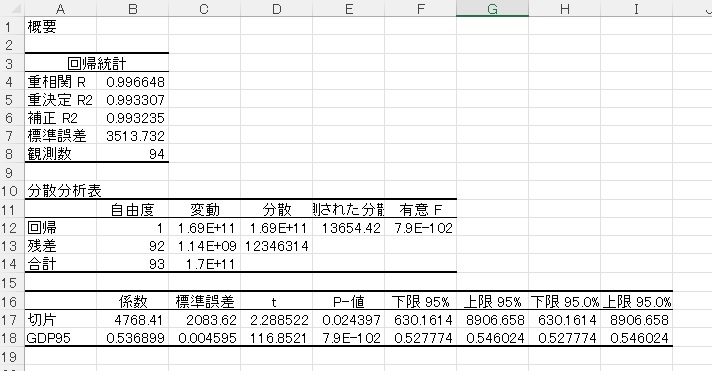
残差の自己相関係数を計算する
残差のデータを使って、残差の自己相関係数を計算します。
残差の1期前のデータは、残差のデータを一行分だけ下にずらすと作れます。セルを一つ分挿入し、下にずらすと簡単にできます。
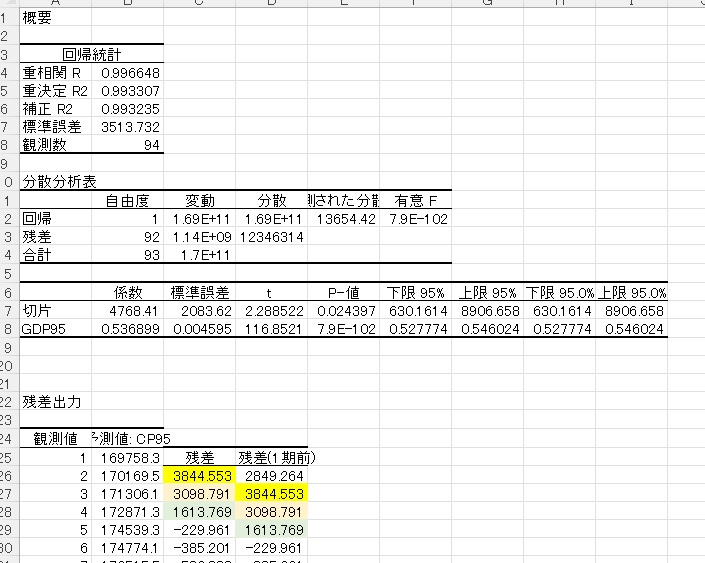
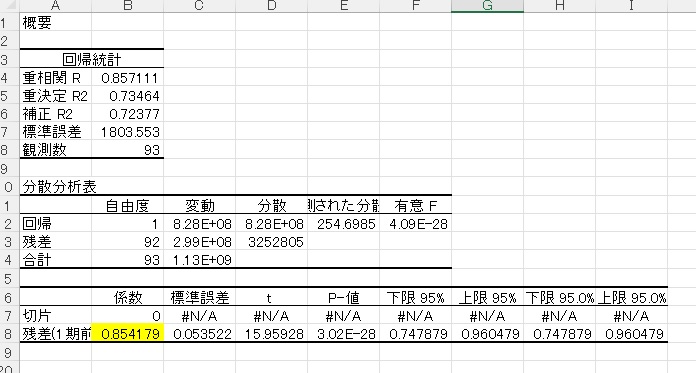
$ u_t=\rho u_{t-1}+ \epsilon_t $の式を推定します。この式には定数項がないので、推計は定数項無しで推定します。「定数に0を使用」にチェックを入れます。
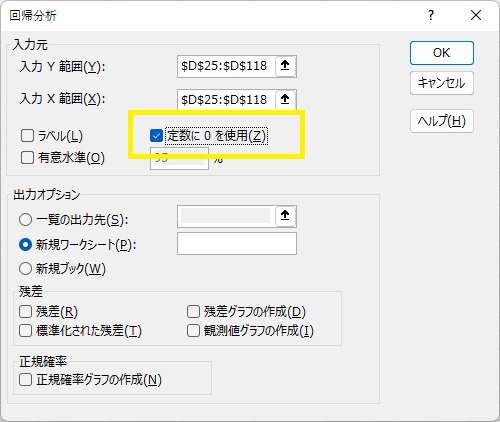
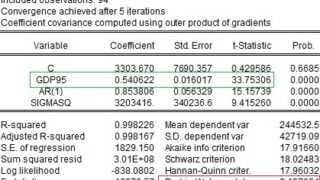
推計結果は以下となります。係数$\rho$は、0.85になることがわかります。1期前の誤差との相関はかなり高いです。
自己相関係数を使って、最小二乗法で計算する。
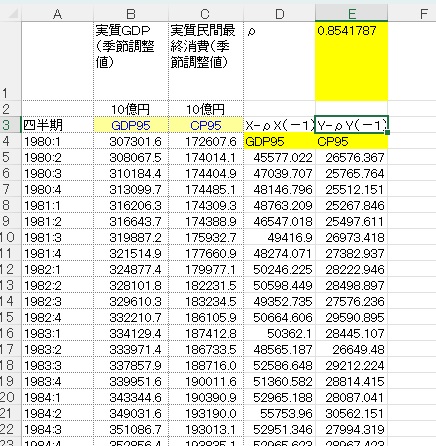
次に、上記で推定した$\rho$を使って、再推定します。ここが作業としては最も面倒です。基本的には、$ X’_t=X_t- \rho X_{t-1} $という形の計算をエクセル上で行います。変形したXとYについて通常の最小二乗法を適用します。
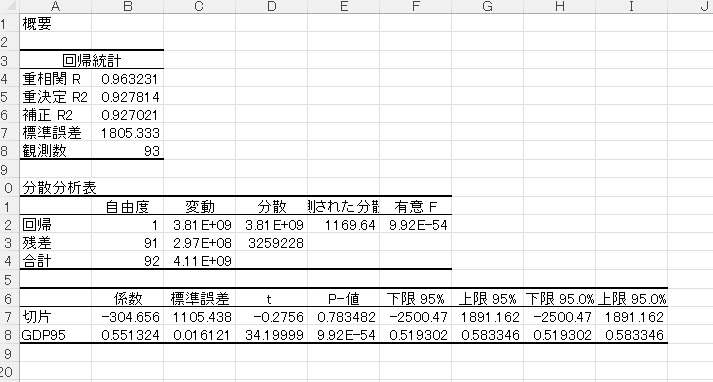
推定結果は以下になります。定数項がマイナスになり、係数が0.54から0.55へと変化しています。元の式の定数項$\alpha$は -304.656/(1-0.8541787)=-2089.24 です。
誤差の動きを見ると、系列相関がなくなっていることがわかります。