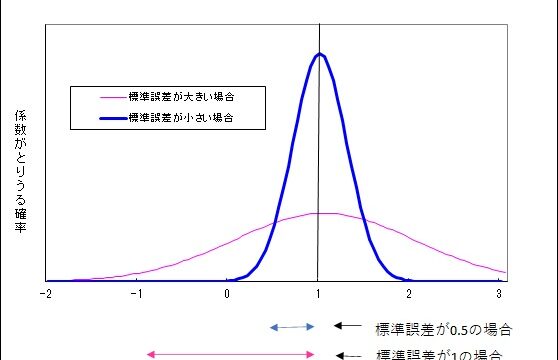
平均は、多数のデータの情報を一つにまとめた代表値の一つです。
- 算術平均
- 加重平均
- 移動平均
- 幾何平均
などがあります。
なぜ平均値が使われるのでしょうか?
代表値が必要なのは、データの分布の様子が一つの値でわかるためです。
たとえば、クラス全体の成績の代表値を考えてみましょう。平均値の他にも、
- 点数を全部足し上げる。
- 最も高得点の人を選ぶ。
といった方法も考えられます。
これらの比べて、平均値が優れているのは、
- 分布全体の中の自分の位置を知りたい
- ほかのクラスと比較したい
といった疑問に答えることができるためです。
算術平均
算術平均はすべての標本を足して、標本数で割るもので、最もよく使われる平均です。データが$a_1,a_2,…,a_n$の時、以下の式で表されます。
$ 算術平均= \dfrac{a_1+a_2+…+a_n}{n}$
平均が望ましくない場合も
平均値が望ましくない場合もあります。平均周辺に多くのサンプルが集まている場合は平均値をとるのが適当ですが、極端な値があるとそれに引きずられてしまいます。
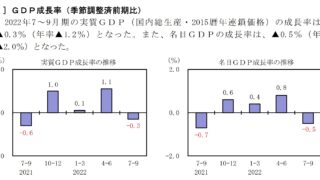
景気に関する統計でも、東日本大震災、新型コロナウイルス感染拡大などの極端な数値があると、平均値は影響されます。一方で、中央値は比較的影響を受けません。
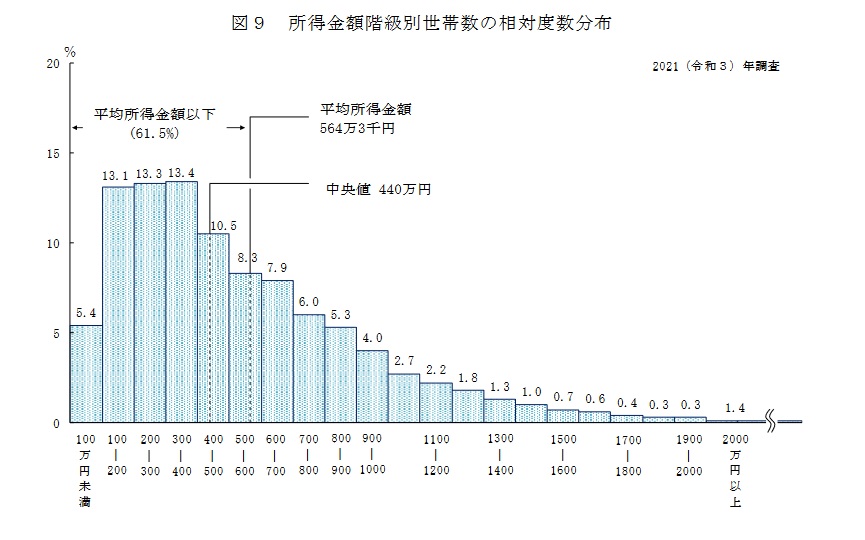
厚生労働省の国民生活基礎調査には所得の分布状況が載っています。平均所得は564万3000円ですが、平均所得以下の世帯は61.5%もいます。少数の高所得者に引っ張られて平均値が上振れしている例です。全世帯を所得順に並べた時真ん中になる数値である中央値は440万円で、こちらの方が代表値としてふさわしいです。
加重平均
加重平均は、足し合わせるときに、重みを変えるものです。データが$a_1,a_2,…,a_n$で、対応する重みが$w_1,w_2,…,w_n$の時、以下の式で表されます。
$ 加重平均= \dfrac{w_1a_1+w_2a_2+…+w_na_n}{w_1+w_2+…+w_n}$
鉱工業生産指数の総合指数は、付加価値額を重みとして、各指数を加重平均することで計算されています。
移動平均
移動平均は、時間の経過とともに、平均する期間を変えるものです。月次指標で移動平均をとる場合、後方移動平均と中心移動平均の2通りの方法があります。データが$a_1,a_2,…,a_t$平均をとる時点を$t$とすると、以下のようにあらわせます。
$ 後方移動平均= \dfrac{a_{t-2}+a_{t-1}+a_t}{3}$
$ 中心移動平均= \dfrac{a_{t-1}+a_t+a_{t+1}}{3}$
最新の値まで使えるので、後方移動平均を使う場合が多いです。ただ、中心移動平均は、元の系列と最大値や最小値はずれないですが、後方移動平均は後ろにずれます。
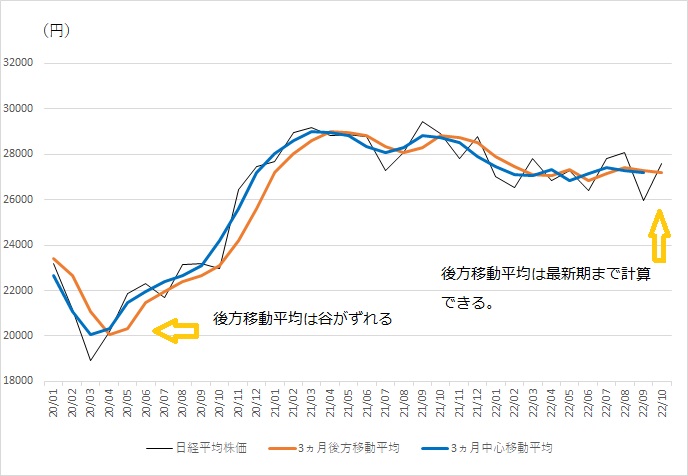
季節調整値は、季節性をならした値ですが、季節調整にも移動平均の考え方が使われいます。
12ヵ月移動平均をとると、年間の季節変動がならされることになります。奇数個の移動平均は簡単で、3か月移動平均は、その月とその前後の月を平均すれば計算できます。しかし、偶数個の移動平均には工夫が必要です。12ヵ月移動平均の場合は以下の手順をとります。
- 前5ヵ月、後ろ6ヵ月で移動平均をとる。
- 前6ヵ月、後ろ5ヵ月で移動平均をとる。
- 2つを平均する。
幾何平均
幾何平均はデータをすべてかけて累乗根をとるものです。データが$a_1,a_2,…,a_n$の時、以下の式で表されます。成長率の平均などに使われます。成長率のデータしか手元にない時、成長率の平均は、比率に変換(1%なら1.01)して幾何平均を取ります。
$ 幾何平均= \sqrt[n]{a_1a_2…a_n} $