平均値の差の検定には以下の3種類が考えられます。
- 研修前、研修後など対応のある場合
- 母分散が等しい場合
- 母分散が等しくない場合
この記事で扱うのは１番目です。
経済統計の使い方では、統計データの入手法から分析法まで解説しています。
研修に効果があったか
この検定が役に立つのは、たとえば、研修前の試験の結果と研修後の試験の結果を比べる場合です。研修を受けた人の研修前後の得点という意味でそれぞれのサンプルには対応がある場合となります。
研修前の試験の結果が70点で研修後の試験の結果が71点だった場合、研修に効果があったと言えるでしょうか？結論は、そのサンプルの分散の大きさによります。分散が大きければ70点と71点は誤差の範囲ですが、分散が小さければ1点の差は大きなものかもしれません。
検定は、研修を受けた人の得点の差を調べて、その差が有意にゼロと異なるかどうかを検定します。差をとったあとは、母平均の検定と同じということです。
手順は以下のようになります。
- 研修前と研修後について、2つの標本があると考えずに、それぞれに人の点数の差を標本と考える（研修前後で点数の差）。
- 点数の差がt分布すると考えて検定する。（母平均の検定と同じ）
- 帰無仮説：点数の差はゼロ
- 対立仮説：点数の差はゼロ以外。
演習問題
無作為に抽出した1番さんから10番さんまでの研修前と研修後の得点です。
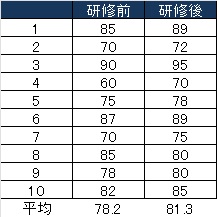
- この結果から、研修に効果があると言えるでしょうか？
- 研修前と研修後の平均点を比較して有意にゼロと違うかどうかを５％有意水準で検定します。
- 「研修後の点数－研修前の点数」をそれぞれ計算します。
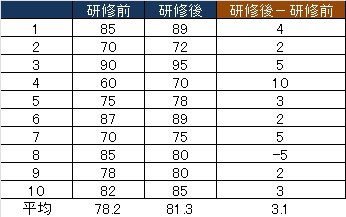
研修前と研修後の差である3.1点というのは、たまたま高くでた数値なのでしょうか、それとも何度サンプルを取り直しても高く出るというものなのでしょか。
3.1点が有意にゼロと違うかどうかを検定します。検定は母平均の検定と同じです。
帰無仮説（研修前後の差はゼロである）を検定する
- 帰無仮説は、「研修前後の得点差はゼロである」です。
- 有意水準を決めます。
- 棄却域を調べます。
- 標本のt値を調べます。
- 仮説を受容するか棄却するかを決めます。
棄却域を求める
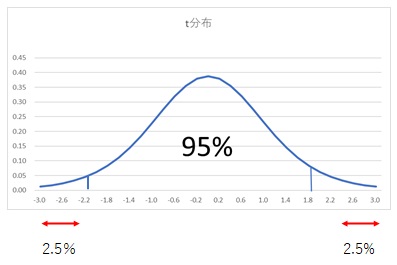
- 有意水準（偶然では起こりえないほど珍しい確率）を決めます。5％以下、１％以下などです。ここでは５％以下とします。
- t分布表から、棄却域を調べます。エクセルのT.INV関数を使います。
- T.INV(「有意水準÷２」,自由度)です。
- 有意水準は５％としましたが、両側合わせて５％とすると、片側は2.5％です。
- t分布の自由度はサンプル数から１を引いたものです。
- T.INV(0.025,10-1)=2.26 なので、棄却域は－2.26以下、2.26以上となります。
標本のt値を調べる
- 標本平均のt値を求めます。式は以下の通りです。
$ T= \frac{ \bar{X} – μ }{\frac{U}{\sqrt{n}} } $
- 標本平均の分布を考えます。
- 母集団の平均はμですが、今回は母集団の平均＝０が帰無仮説です。
- 分散は不偏分散を使います。
- Xを標準化したものは、自由度n-1のｔ分布に従います。
- これを計算すると、－2.63になります。
まとめ
- 母集団の平均＝ゼロの帰無仮説を検定する。
- 有意水準の５％の両側検定では棄却域は-2.26以下、2.26以上となる。
- 標本からｔ値を計算すると-2.63
- 棄却域に入るので、帰無仮説を棄却できる。
- 研修前後での得点差は有意にゼロと異なる。
- 研修に効果はあった。
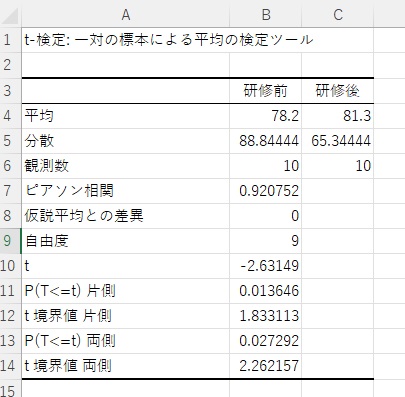
エクセルで計算すると簡単
エクセルで、分析ツールを使うと、簡単に計算できます。上の研修データを使います。
分析ツールを有効にする方法は以下の記事にあります。
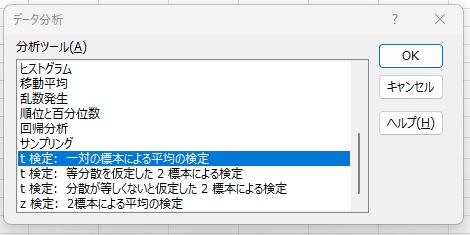
分析ツールで、t検定：一対の標本による平均の検定を選びます。
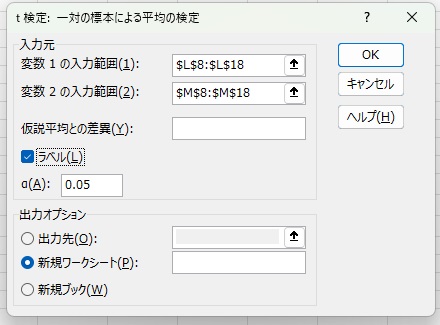
変数1と変数2に範囲を指定します。変数名も一緒に範囲指定しているときは、ラベルにチェックを入れます。５％で両側検定するので、aは0.05のままにします。
新規ワークシートに結果が出てきます。ｔ値は-2.63、境界値は2.26以下、2.26以上だということがわかります。
- 分析ツールの紹介
- 【Python】Pythonの基本操作
- 経済学Q＆A（試験編）
- 【経済統計】消費をみるために必要な月次指標ベスト３｜消費総合指数、商業動態統計、家計調査
- 経済統計チャットボット マホナ
