この記事では、経済統計を読み解くうえで基本的な知識について解説します。経済データにもさまざまな種類があります。分析しようとしているデータがどのような性質のデータかを知る必要があります。
また、前年同期比、季節調整など、聞いたことはあるけれど、よくわかってないという言葉について、理解が深まります。
経済統計の使い方では、経済統計の入手法から分析法まで解説しています。

時系列データとクロスセクションデータ
経済統計の多くは時間とともにデータが蓄積される時系列データです。しかし、クロスセクションデータも有用です。ある時点での、県別のデータや企業別のデータが発表されることがあります。これらはクロスセクションデータと呼びます。時系列データとともに、クロスセクションデータがあるものをパネルデータと呼びます。
期種・期間
時系列データでは、まずその統計がどのくらいの頻度で発表されているものかが重要です。頻度を表すことを期種といいます。為替レートや株価は毎日発表されるので日次統計です。鉱工業生産指数や消費者物価指数など月次で発表されるものも多いです。GDP統計や日銀短観は四半期に一度発表されます。市街地価格指数は半年に一度発表されます。予算は年度(4月~翌3月)の統計です。GDPの年次推計の中には、暦年(1月~12月)のデータも多くあります。
フローとストック
経済データの種類として重要な分類法は、フローデータかストックデータかということです。水道にたとえれば、ある一定時間に落ちた水の量がフローのデータで、ある一時点にたまっている水の量がストックのデータです。基本的には前期のストックのデータにフローのデータを足したものが当期のストックのデータになります。その期間に失われたストックの部分(減耗分)は差し引きます。
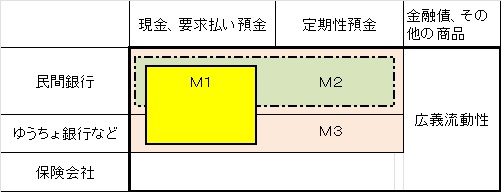
フローとストックの関係をみると、GDPがフローのデータであるのに対し、国富がストックのデータになります。設備投資がフローのデータで、それを積み重ねたものが資本ストックです。毎月供給される現金や預金がフローのデータで、マネーストックはストックのデータになります。
| フロー | ストック |
| GDP | 国富 |
| 設備投資 | 資本ストック |
| 現金の発行額、預金の増加額 | マネーストック |
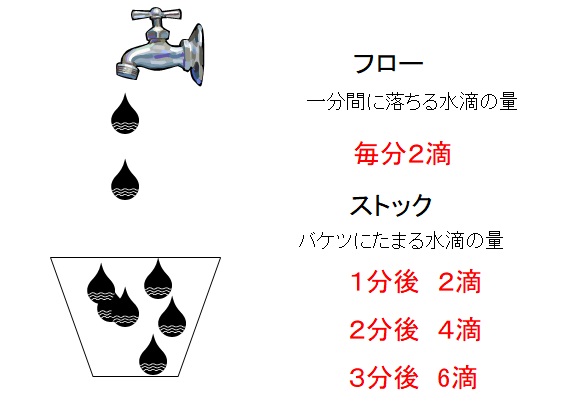
下の図では、水道から水滴が落ち、バケツにたまっていく様子を書いたものです。毎分2滴の水滴が落ちるとしたら、毎分ごとにデータをとると、2滴という量が観察されます。これがフローのデータです。一方バケツの中をみると、1分後のデータは2滴、2分後のデータは4滴、3分後には6滴となるでしょう。実際には水滴ではなく水としてたまって行くので適切なたとえではないですが…
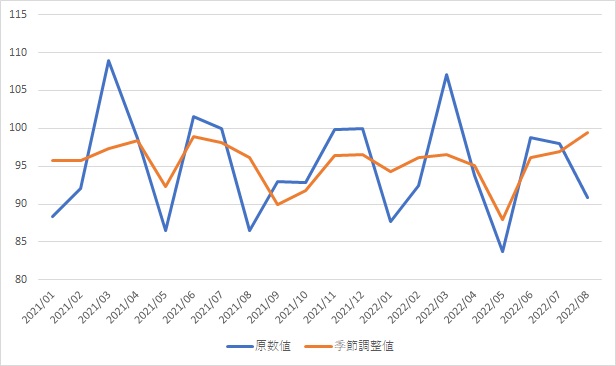
原数値と季節調整値
月別、四半期別のデータは、季節によって大きく変動している場合があります。鉱工業生産指数は、5月のゴールデンウイークや8月のお盆休みには減り、決算期の3月に増えるという規則性があります。これらのデータをみただけでは趨勢がつかみにくい場合が多いので、季節調整値を作成します。データから季節的な変動パターンを取り出して、その部分を除いた系列を作成します。季節調整は、複雑な統計処理で作成されますが、米商務省センサス局が開発したX-12-ARIMAという季節調整法を使うことが多いです。
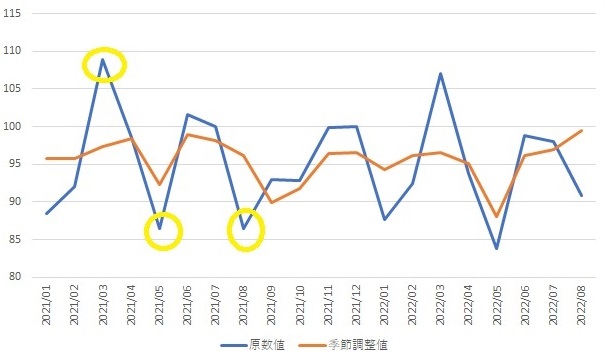
前期比と前年同期比
データの加工として重要なのは伸び率を見ることです。ある基準時点より何%データが増えているかをみるものです。年次データですと、前年と比べる前年比を見ることが多いですが、月次データ、四半期データでは、1期前のデータと比べる場合と1年前のデータを比べる場合があります。1期前のデータと比べる場合を前期比(月次の場合は前月比)、1年前の同じ期のデータと比べる場合を前年同期比(月次では前年同月比)と呼びます。
季節性の大きいデータの前期比をみても、季節変動の大きさに邪魔されて本来の動きがわからないので、季節調整済みのデータの前期比をみます。一方、前年同期比の場合は、前の年と同じ期を比べるので原数値で比較することができます。
前年同期比のデータの法が、滑らかに動き、その系列の大きな流れをつかむには適しています。前期比は前の比べた細かな動きを見ることができるので、直近での方向性を判断する場合に優れています。
前期比年率
GDP統計では、前期比のデータで伸びがどの程度かを把握しますが、四半期のデータで前の四半期と比べてどのくらい伸びたかでは、伸び率を聞いてもピンときません。年間の変化率で把握することが多いためです。
そこで、前期比の伸びが1年間続いたらどの程度の伸びになるかも発表しており、前期比年率と呼びます。前の四半期から今期どれだけ伸びたかを示すので「瞬間風速」という別名もあります。
四半期の伸びの4期分ですので、大まかに言えば、前期比の4倍の値になりますが、単に4倍するだけでは求まりません。たとえば1-3月の前期比が2%だったとしましょう。この伸びは、4-6月期には2%伸びた分(1.02)の2%伸びることになります(1.02×1.02=1.0404)。こう考えると、1年間の伸びは1.02を4回かけたものつまり1.024=1.08243216です。2%の4倍である8%に近いですが、正確には8.24%となるわけです。
寄与度
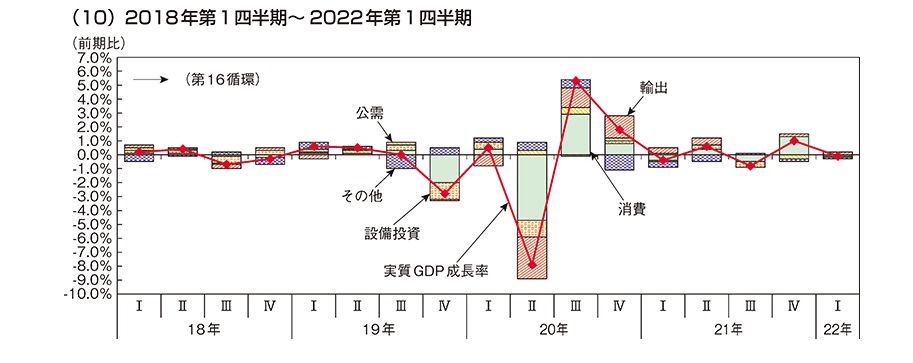
もう一つ重要な考え方が寄与度です。寄与度とは、ある系列がいくつかの構成要素からできているときに、各構成要素が全体の伸びにどれくらい寄与したかを表すものです。
たとえば、GDPを大まかに、民間需要、公的需要、海外需要からできているとすると、それぞれの構成項目がGDPの伸びに対してどの程度寄与したかを表します。各需要の寄与度を加えたものはGDPの伸びに等しくなります。
各構成要素の伸び率をみることで、各要素の動きを把握することができますが、寄与度の優れている点は、全体の伸びに対する貢献度を表している点です。構成要素のうち高い伸びのものがあっても、構成比が小さいと、寄与度は小さくなります。
<寄与度の考え方>
実質GDP=民間需要+公的需要+海外需要
↓
実質GDPの増加分=民間需要の増加分+公的需要の増加分+海外需要の増加分
↓
$ \dfrac{実質GDPの増加分}{1期前の実質GDP}=\dfrac{民間需要の増加分}{1期前の実質GDP}+\dfrac{公的需要の増加分}{1期前の実質GDP}+\dfrac{海外需要の増加分}{1期前の実質GDP} $
↓
実質GDPの増加率=民家需要の寄与度+公的需要の寄与度+海外需要の寄与度