最小二乗法は、$Y_i=\alpha+\beta X_i+e_i$という関係を想定して推定します。$X$と$Y$の散布図を描くと直線の関係にある場合です。しかし、こうした直線の関係になくても$X$を加工することで、さまざまな変数の関係を推定することができます。
経済統計の使い方では、統計データの入手法から分析法まで解説しています。
基本の形
基本の形は、$Y$と$X$が線形（1次式）を想定しています。
$Y_i=\alpha+\beta X_i+e_i $
これは、$X$と$Y$の散布図を描くと直線状に並んでいることを表します。
たとえば、$Y_i＝10＋２X_i$は以下のグラフです。誤差は除いているので、直線に並んでいます。
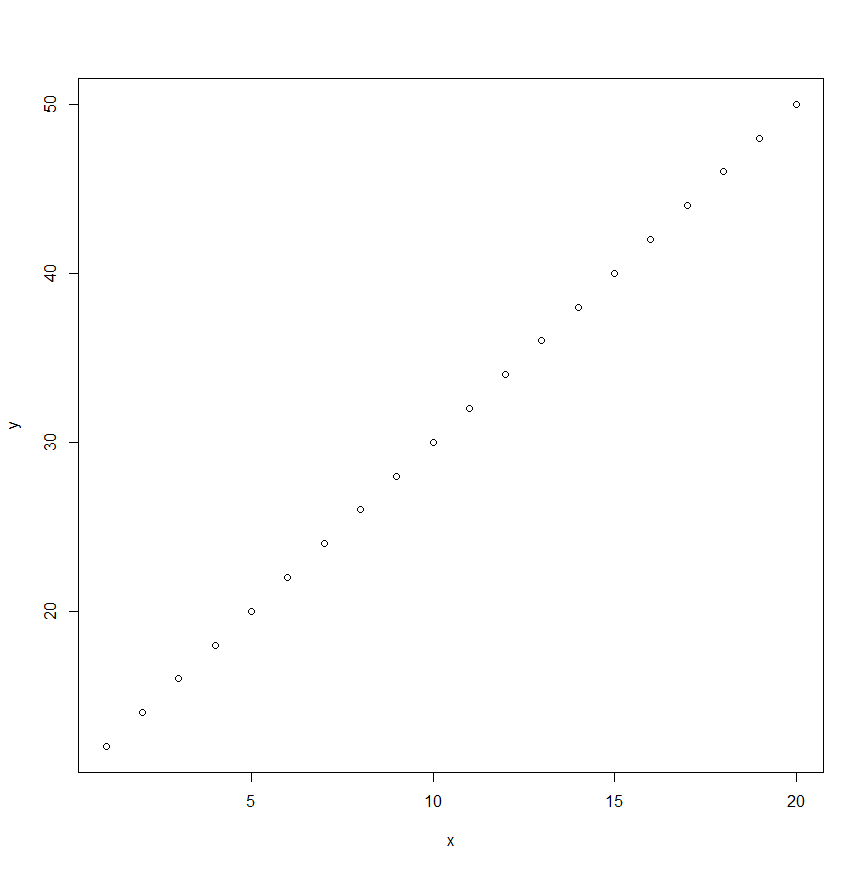
グラフはRで描いています。xに１から20までの数字を作り、ｘを加工してyを作成し、plotコマンドで散布図を描いています。以下のグラフもy<-10+2*xのｘを変形して描いています。
x <- 1:20
y <- 10+2*x
plot(x,y)逆数
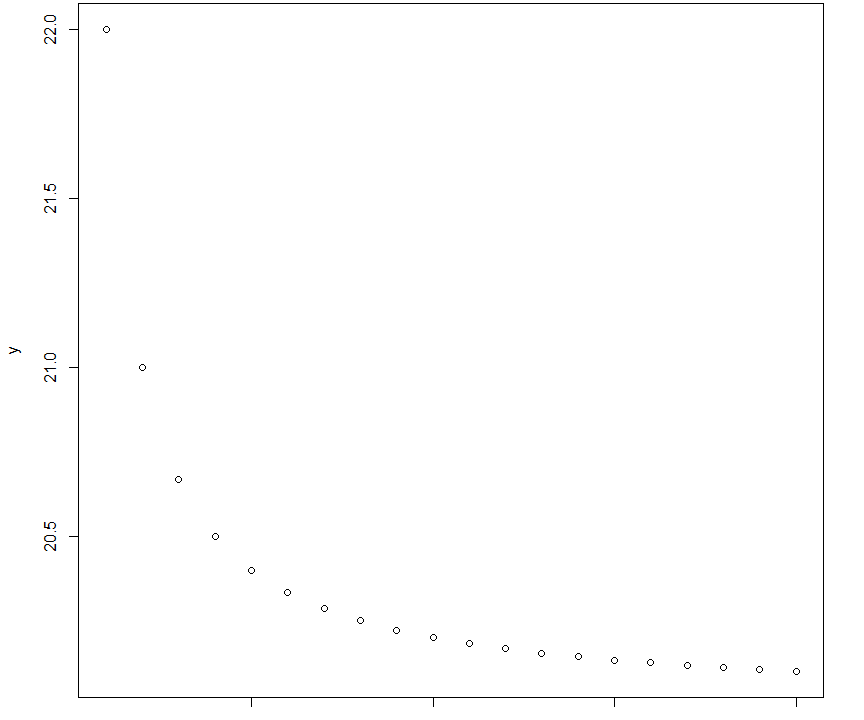
基本は線形ですが、$X_i$を加工することで、さまざまな関数を表すことができます。たとえば、$X_i$を逆数（$1/X_i$）に加工した計算式$Y_i=10+2 (1/X_i) $の散布図を描くと以下のような双曲線になります。経済学ではフィリップスカーブ（物価と失業率の関係）がこの関係にあたります。$1/X$を説明変数にして最小二乗法を適用すると、散布図が双曲線になる変数が推定できることがわかります。
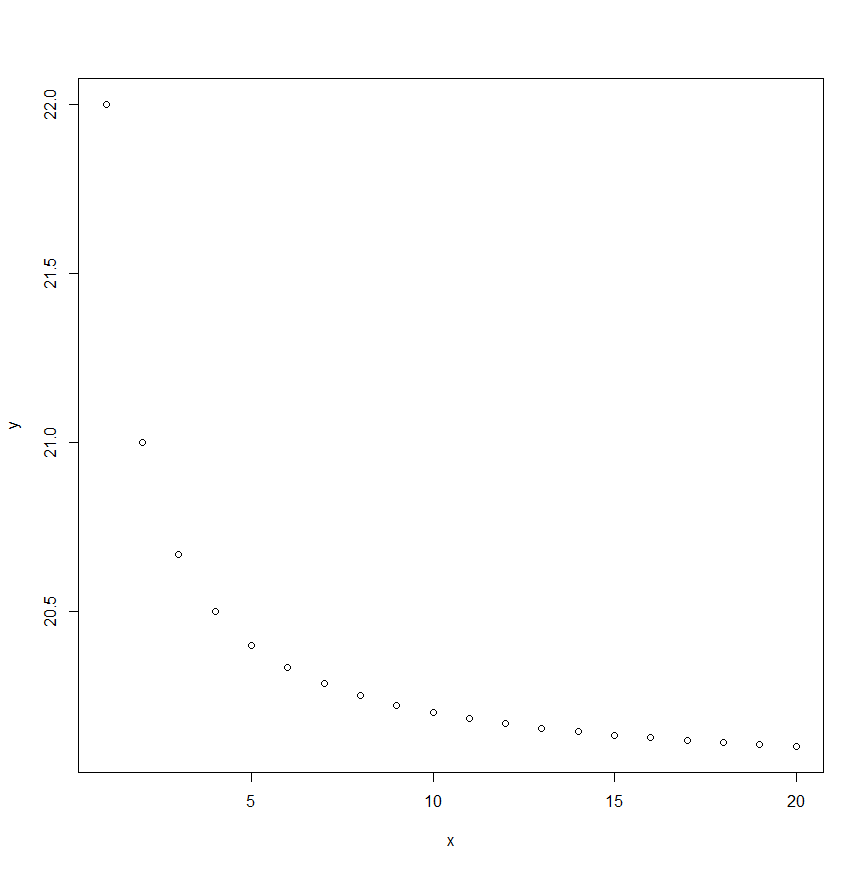
このようにして、$X$と$Y$が直接線形の関係になくてもXを加工すればさまざまな関数を推定できます。
グラフはRで描いています。
x <- 1:20
y <- 10+2*1/x
plot(x,y)２次関数
$Y_i=\alpha+\beta X_i^2 +e_i$
散布図が以下のような形なら$Y$は$X$の２次関数になっています。
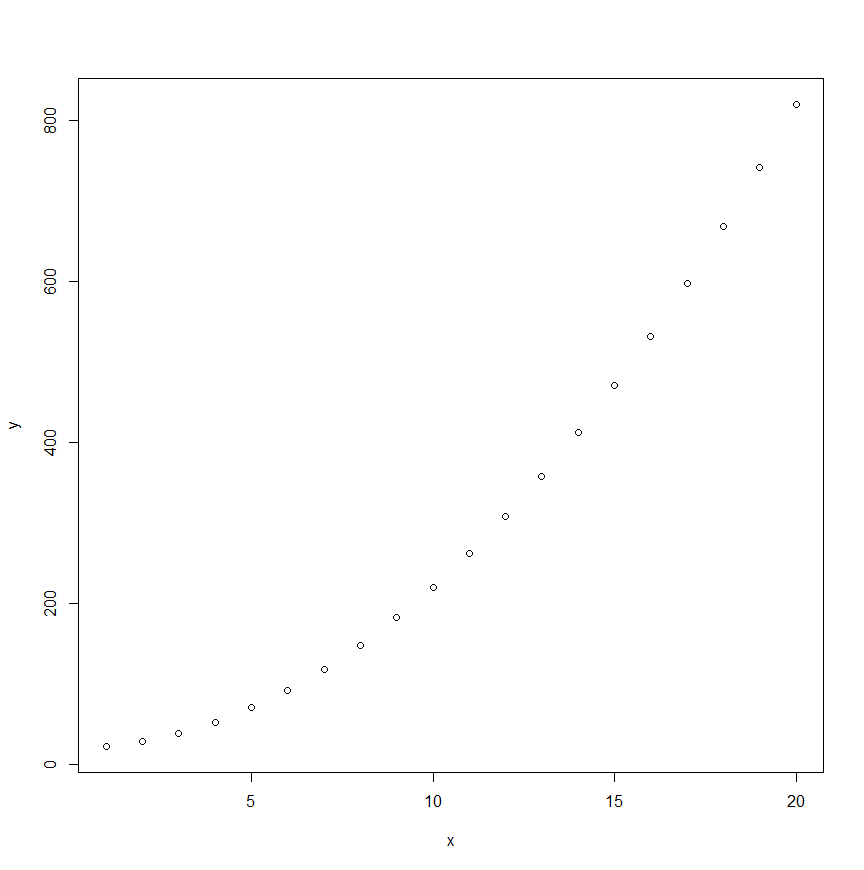
グラフはRで描いています。
x <- 1:20
y <- 10+2*x^2
plot(x,y)対数関数
$Y_i=\alpha+\beta \log{X_i} +e_i$
散布図が以下のような形なら$Y_i$は$X_i$の対数関数になっています。
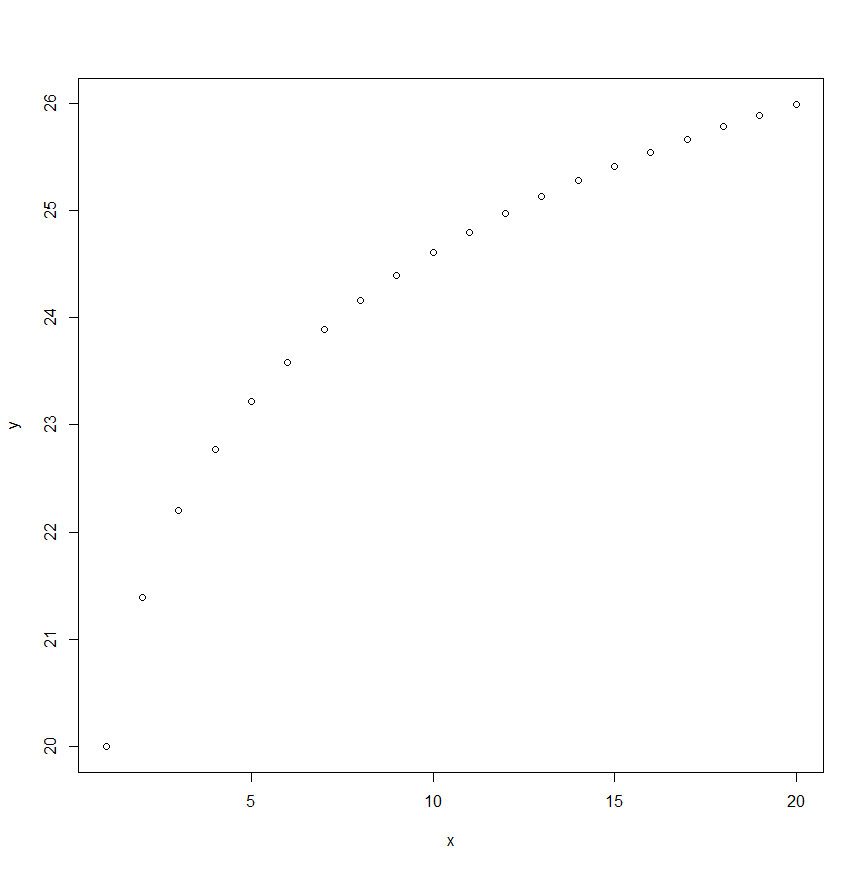
グラフはRで描いています。
x <- 1:20
y <- 10+2*log(x)
plot(x,y)指数関数
$Y_i=\alpha+\beta e^{X_i} +e_i$
散布図が以下のような形なら$Y_i$は$X_i$の指数関数になっています。
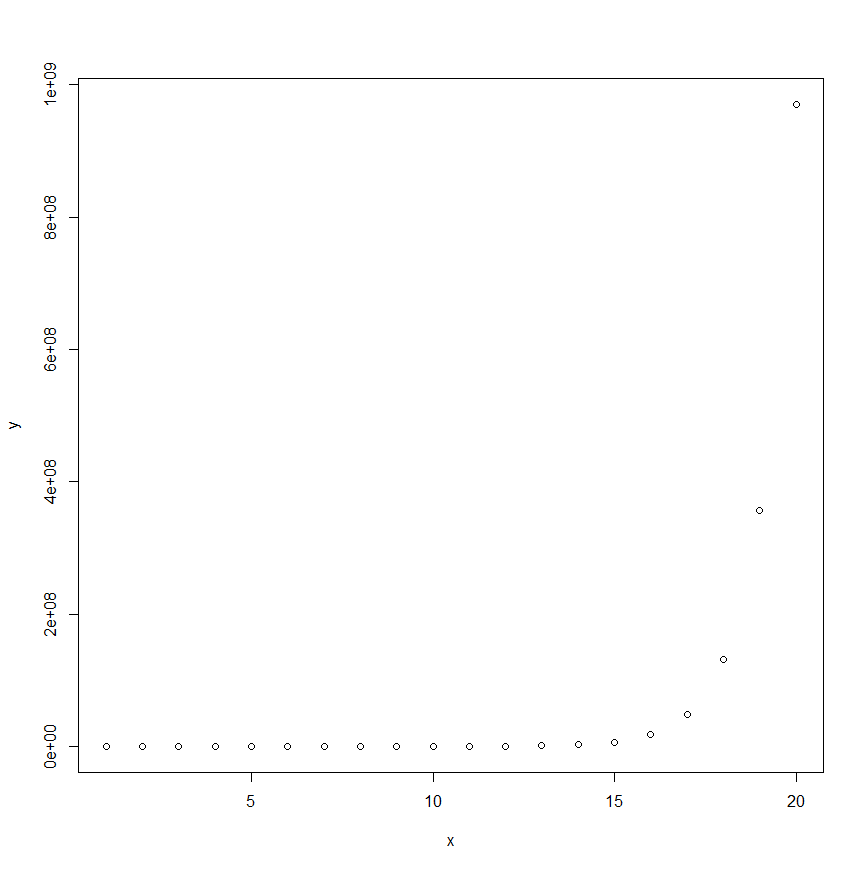
グラフはRで描いています。
x <- 1:20
y <- 10+2*exp(x)
plot(x,y)平方根
$Y_i=\alpha+\beta \sqrt{X_i} +e_i$
散布図が以下のような形なら$Y_i$は$X_i$の平方根となっており、無理関数になっています。
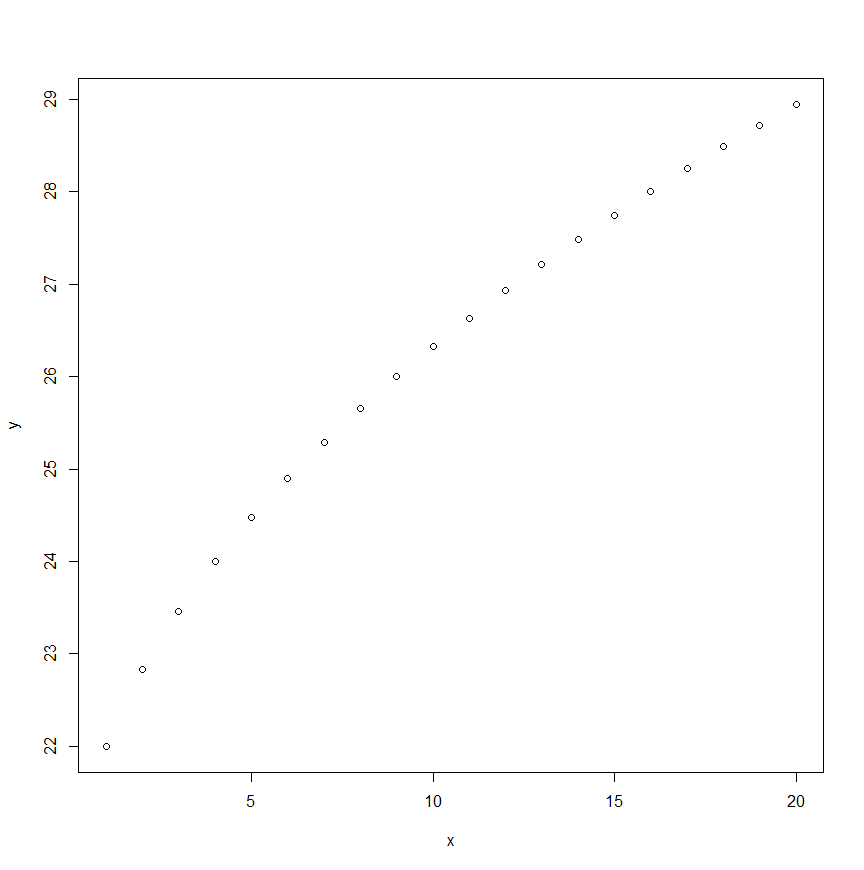
グラフはRで描いています。
x <- 1:20
y <- 10+2*sqrt(x)
plot(x,y)まとめ
- 最小二乗法は線形を仮定しています
- $X_i$を加工することでさまざまな関数計を推定できます
- 逆数、２次関数、対数関数などがあります
- 【時系列分析】課題３ ドリフト付きランダムウォーク
- 【時系列分析】課題２ グレンジャーの因果関係
- 【時系列分析】課題１ 為替レートの予測
- 「回帰分析から学ぶ計量経済学」を使ったセミナーを行います(2024年３月８日）
- 正誤表 回帰分析から学ぶ計量経済学
