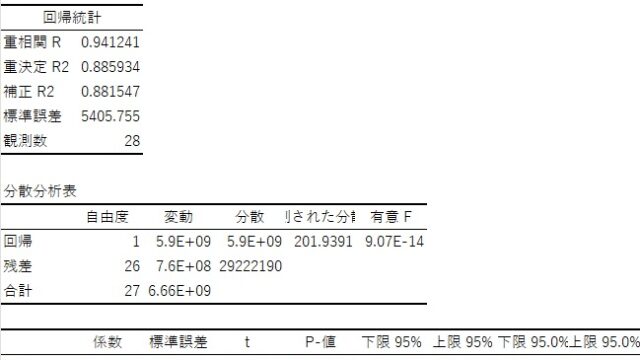
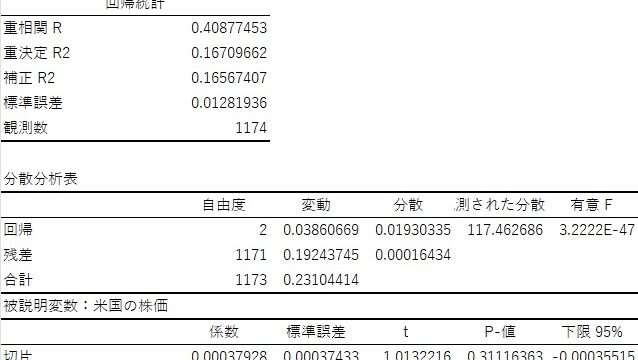
経済統計の使い方では、統計データの入手法から分析法まで解説しています。
誤差項に自己相関がある場合
通常の最小二乗法は以下の式を推計します。
$ Y_t= \alpha + \beta X_t + u_t $
誤差項に自己相関（前期の値との相関）がある場合は、誤差項に関して以下の式が成り立つことになります。
$ u_t=\rho u_{t-1}+ \epsilon_t $
誤差項に自己相関がある場合は、誤差の動きがランダムにならず、プラスの値の時はプラスの値が続き、マイナスの値の時はマイナスの値が続きます。系列相関があるとも呼びます。
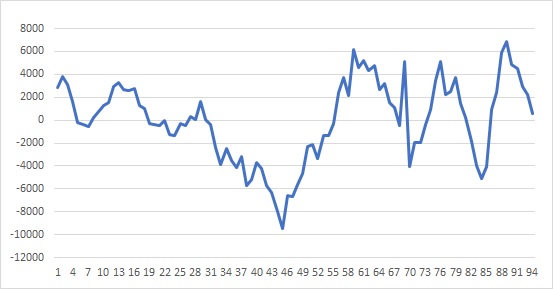
誤差項に自己相関があるということは、最小二乗法が最適な推定値になるための仮定の一つである「誤差項に自己相関がなく、均一である」が満たされないことになります。不均一分散の一つで、誤差が過少評価されてしまいます。ｔ値が過大評価され、有意でない係数を有意であると判定する危険性ができきます。
ダービンワトソン比で検証
系列相関があるかどうかは、ダービン・ワトソン比で検証します。誤差項に自己相関があるかどうかを調べたものです。
誤差項と誤差項の1期前との相関係数は以下の式で求められます。相関係数の元になる共分散は、平均からの偏差の二乗を計算しますが、誤差の平均はゼロなので、変数の二乗和を使えばよいです。
$ 誤差項の１期前との相関係数=\dfrac{\sum{u_i}{u_{i-1}} }{\sum u_i^2}$
ただ、小標本ではこの方法では検定できないため、ダービン・ワトソン比を使います。ダービン・ワトソン比は以下の式で表されます。
$ DW=\dfrac{\sum({u_i}-{u_{i-1}})^2 }{\sum (u_i)^2} $
これは以下の式に展開できます。
$ DW=\dfrac{\sum{u_i}^2-2 \sum{u_i u_{i-1}}+ \sum{u_{i-1}^2} }{\sum (u_i)^2} $
$ =\dfrac{\sum{u_i}^2}{\sum u_i^2} + \dfrac{\sum{u_{i-1}^2} }{\sum u_i^2}-2\dfrac{ \sum{u_i u_{i-1}}}{\sum u_i^2} $
大標本であれば、$\sum{u_{i-1}}$ は $\sum{u_i}$と等しいと考えられるので、以下の式となります。
$ DW \fallingdotseq 2(1- \rho )$
ダービン・ワトソン比は、大標本では、相関係数の関数と考えられます。
誤差項に自己相関がない場合は２を示し、正の相関が強いと０に近づき、負の相関が強いと４に近づくということです。
コクラン・オーカット法などで対処
誤差項に自己相関がある場合、コクラン・オーカット法などで対処することになります。
コクラン・オーカット法では、残差から$\rho$を計算し、それを使って元の式を再現する方法をとります。こちらについては、以下の記事をご覧ください。
元の式に残差の式を入れて一括して推計することも考えられます。最小二乗法では推計できませんが、最尤法などを使えば計算できます。
EViewsでは、説明変数の後にAR(1)を加えれば、誤差項の系列相関を含めた係数を最尤法で計算します。以下の例は、山澤成康『実戦計量経済学』で使ったものです。
まず、通常の最小二乗法で推計します。ダービン・ワトソン比は0.28なので、系列相関があることがわかります。
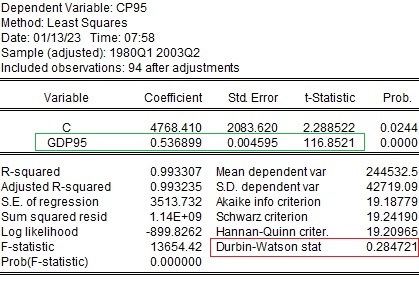
次に系列相関を想定した場合の結果です。説明変数にAR（１）を加えており、$\rho$は0.85であることがわかります。上記推計との違いは、ｔ値に表れます。係数はほぼ変わりませんがｔ値がかなり小さくなっています。ダービン・ワトソン比も２に近づいています。
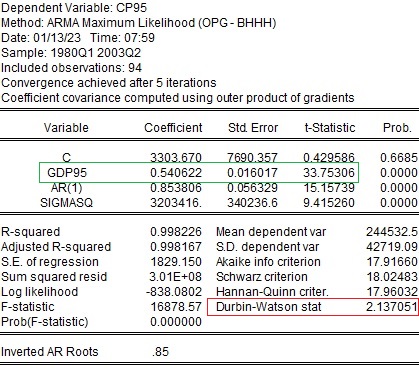
| 通常の最小二乗法 | 系列相関を考慮した場合 | |
| GDP95の係数 | 0.54 | 0.54 |
| GDP95の標準誤差 | 0.005 | 0.016 |
| GDP95のｔ値 | 116.9 | 33.8 |
| ダービンワトソン比 | 0.28 | 2.14 |
まとめ
誤差項に自己相関がある場合の対処法について解説しました。誤差項に系列相関があると、t値などが過大になり、本来有意でない係数を有意と判断してしまう危険性があります。
系列相関があるかどうかは、ダービン・ワトソン比で判定します。２に近ければ系列相関はなく、０に近ければ正の系列相関、４に近ければ負の相関係数があります。
系列相関がある場合は、コクラン・オーカット法などを使って、系列相関を前提とした推計をします。
- 経済学Q＆A（試験編）
- 【経済統計】消費をみるために必要な月次指標ベスト３｜消費総合指数、商業動態統計、家計調査
- 経済統計チャットボット マホナ
- 経済金融指標の見方 Q&A２
- 経済金融指標の見方 Q&A
