【計量経済学】最小二乗法の推定誤差|標準誤差とｔ値

最小二乗法を推計すると、係数が推定できます。基本的にはどんなデータでも係数は推定できますが、その係数が信頼できるとは限りません。誤差の範囲が広ければ、係数がゼロ、つまりその説明変数が被説明変数に影響しない可能性があります。これを調べるために、係数の標準誤差を計算します。

また、係数がゼロでないかどうかを調べるうえでは、単位に左右されないｔ値が有用になります。

経済統計の使い方では、統計データの入手法から分析法まで解説しています。

最小二乗法の基本的な形は以下とします。サンプルを表す小文字は除いています。

$ 　　　Y=\alpha + \beta X + e $

サンプル数はn、定数項を含む係数の数をK、Xの平均を$ \bar{X}$ とします。

Contents

推定式の標準誤差

推定結果全体にどの程度誤差があるかは、誤差項の動きを見ます。誤差の平均はゼロですが、各サンプルで誤差が大きければ誤差の標準偏差は大きくなります。

推定値の誤差の分散は、サンプルから計算された誤差の不偏分散を求めることです。平均はゼロなので誤差の二乗和を自由度で割ったものになります。推定値の標準誤差は、不偏分散の平方根です。サンプル数がn、定数項を含む係数の数をKとすると以下のように書けます。

$ 推定値の標準誤差＝\sqrt{ \dfrac{\sigma^2}{ n-K} } $

係数の標準誤差は単回帰の場合、以下の形です。

$ 係数\betaの標準誤差= \sqrt{ \dfrac{\sigma^2}{ \sum_{i=1}^{n} （X_i-\bar{X})^2}} $

分母は、$X$の偏差の二乗和で、$X$の分散を計算する際の分子の部分です。このため、$X$の分散が大きければ、係数の標準誤差は小さくなるという関係にあります。

重回帰の場合は、定数項の列（すべて１）を含んだXの要素が縦に並んだ行列をXとして、以下のように書けます。計算されて出てくるのは、分散共分散行列です。使用するのは対角要素で、係数の標準誤差はそれぞれの平方根です。

$ 係数の分散ベクトル（標準誤差は平方根）＝\sigma^2(X’X)^{-1} $

少しわかりにくいかもしれませんので、$X$を1列目が１、2列目が説明変数$X１（1,2,3,4,5)$、3列名が説明変数$X２(5,-5,5,-5,5)$、サンプル数が５として表してみます。

$ X= \begin{pmatrix} 1 & 1 & 5 \\
1 & 2 & -5 \\
1 & 3 & 5 \\
1 & 4 & -5 \\
1 & 5 & 5 \end{pmatrix} $

$(X’X)^{-1}$は、定数項を含む変数の数分（3個）の行列になり、係数の分散はこの行列の対角要素を使って計算します。

$ (X’X)^{-1}= \begin{pmatrix}
1.11 & -0.30 & -0.01 \\
-0.30 & 0.10 & 0.00 \\
-0.01 & 0.00 & 0.01
\end{pmatrix} $

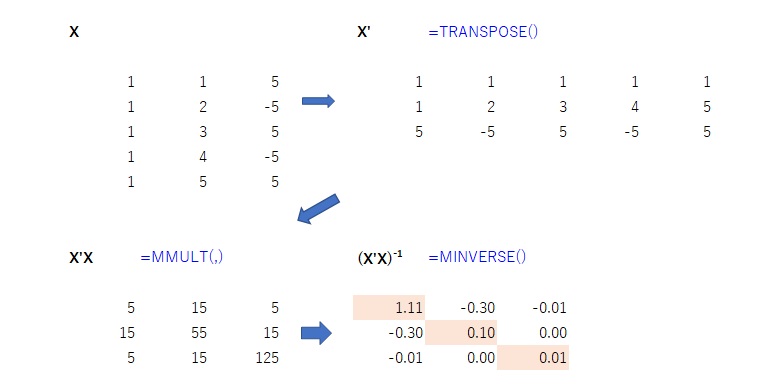
エクセルを使って行列計算の計算過程を示すと以下のようになります。転置行列はTRANSPOSE関数、行列の積はMMULT関数、逆行列はMINVERSE関数を使います。

t値は、係数を係数の標準誤差で割ったものです。

$ t値＝\dfrac{係数}{係数の標準誤差} $

係数が係数の標準誤差の何倍あるかを表してることになります。係数の分布を考えると、係数の値から前後標準誤差の2倍の範囲で95％以上を占めることになります。この範囲内にゼロがなければ、係数がゼロでない可能性が高いことを表します。

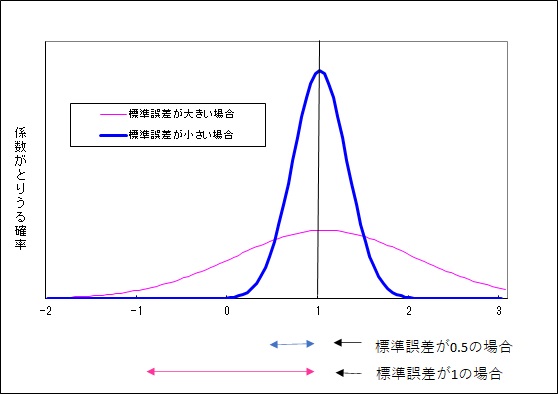
下のグラフで説明しましょう。係数が１と推定され、それがゼロである可能性があるかどうかを検討します。青の線で描かれた分布の場合、標準誤差が0.5でｔ値は２となります。この場合は、ゼロとなる可能性はかなり少ないことがわかります。

一方、ピンクの線で描かれた分布の場合、標準誤差が１でt値は１となります。係数がとりうる分布にゼロが入っています。つまり係数がゼロである可能性を否定できないということです。

以下が記事のまとめです。

	式の形
推定値の標準誤差	$ \sqrt{ \dfrac{\sigma^2}{ n-K} } $
係数の標準誤差（単回帰）	$ \sqrt{ \dfrac{\sigma^2}{ \sum_{i=1}^{n} （X_i-\bar{X})^2} }$
係数の標準誤差（重回帰）	$ \sqrt{ \sigma^2(X’X)^{-1} } $
ｔ値	$ \dfrac{係数}{標準誤差} $