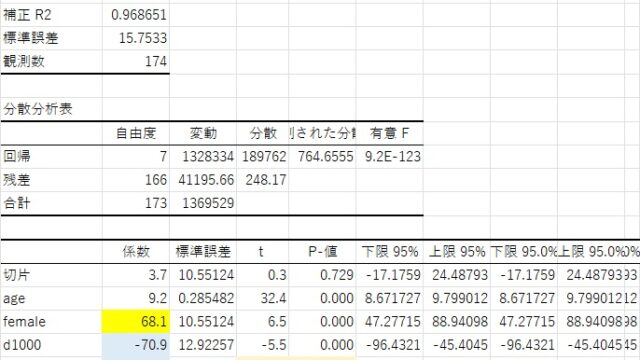
最小二乗法の計算は、エクセルでもできるので、系列を指定すれば結果は得られます。ただ、どのような仕組みになっているのかを知っておくのも重要です。
多くの教科書では、簡単に計算できる説明変数が一つの単回帰の例は載っていますが、説明変数が複数ある場合は、行列計算が必要なので、結果だけ載せている場合や載せていない場合が多いです。
この記事では、行列計算にあまりなじみがない人でも、だいたいどんなことをやっているかをわかるようにしたいと思います。
経済統計の使い方では、統計データの入手法から分析法まで解説しています。

重回帰式の行列表示
重回帰式は以下の形で書けます。
$y=\alpha + \beta_1 x_1 +\beta_2 x_2 + e $
$y$と書いていますが、詳しく描くと添え字が必要で$y_i$と表し、その中身は、変数の数を$n$とすると、$y_1,y_2, \cdots y_n $になります。
これを行列表示で表すと以下になります。大きな違いは、行列$\mathbf{X}$の左1列は1だけで、定数項の部分を表します。
$ \mathbf{ Y= X b +e } $
これを要素を含めて描くと以下のことを表しています。
$\begin{pmatrix}
y_1 \\ y_2 \\
\vdots \\ y_n
\end{pmatrix}=
\begin{pmatrix}
1 & x_{11} & x_{21} \\ 1& x_{12} & x_{22} \\
\vdots & \vdots & \vdots \\
1 & x_{1n} & x_{2n}
\end{pmatrix} \begin{pmatrix}
\alpha \\ \beta_1 \\ \beta_2
\end{pmatrix}+\begin{pmatrix}
e_1 \\ e_2 \\
\vdots \\ e_n
\end{pmatrix} $
係数の求め方
行列による最小二乗法の計算について解説します。必要なのは、転置行列の計算と行列の微分に関する知識です。微分ですら難しいのに、さらに行列の微分が必要になり、難解です。こんなものか、ということでよいのではないかと思います。
被説明変数が$\mathbf{Y}$、説明変数が$\mathbf{X}$である次の式を想定して、誤差の二乗和を最小にするようなパラメーターのベクトル$\mathbf{b}$を求めます。
$ \mathbf{Y=Xb+e } $
残差の二乗和の計算
残差の二乗和は$\mathbf{e’e}$と表すことができます。最小二乗法では、これを最小にする係数を求めます。
$ \sum_{t=1}^n e_t^2=e_1^2+ e_2^2 +e_3^2+ \dots + e_n^2
=\begin{pmatrix}
e_1 & e_2 & e_3 & \dots & e_n
\end{pmatrix}
\begin{pmatrix}
e_1 \\ e_2 \\ e_3 \\ \vdots \\ e_n
\end{pmatrix}
= \mathbf{e’e}
$
係数を求めるために、残差の二乗和を$\mathbf{Y}$と$\mathbf{xb}$で表します。
$ \mathbf{e’e} =(\mathbf{Y-X b } )'(\mathbf{Y-X b } ) $
転置行列の性質($\mathbf{ (A+B)’ = A’+B’ }$ 、$\mathbf{ (AB)’ = B’A’ }$ )から、$(\mathbf{Y-X b } )’=(\mathbf{Y’-(X b)’})=( \mathbf{Y’-b’X’})$なので、以下の式が成り立ちます。
$ \mathbf{e’e} = ( \mathbf{Y’-b’ X’ } )( \mathbf{Y – X b })
\begin{equation}
= \mathbf{ Y’Y -Y’X b -b’ X’ Y + b’ X’X b }
\end{equation} $
これを微分してゼロと置けばいいわけですが、式が結構長いですね。もう少しまとめることを考えます。$\mathbf{Y’Y}$は定数なので微分すれば消えます。$ \mathbf{b’ X’X b}$は2次形式の微分が使えます。方針は$\mathbf{Y’X}$と$\mathbf{X’Y}$を一つにまとめることです。
$\mathbf{Y’X}$と$\mathbf{X’Y}$を一つに
$\mathbf{Y’Xb}$の計算結果はスカラー(一つの数値)になります。その理由を説明します。
定数項を含む$\mathbf{X}$の変数は3つなので、$\mathbf{Y’X}$は(1×3)行列です。これに$\mathbf{b}$(3×1)ベクトルをかけると一つの数値になります。一つの数値は1行1列の行列とみなせるので、転置しても同じ値になります。
つまり$\mathbf{Y’Xb=(Y’Xb)’}$です。
次に$\mathbf{(Y’Xb)’}$のカッコを取ることを考えます。転置行列の性質と「転置行列の転置行列はもとの行列」であることを使えば、$\mathbf{(Y’Xb)’=(Xb)'(Y’)’=b’X’Y}$となります。つまり次の式が成り立ちます。
$\begin{equation}
\mathbf{Y’X b = b’ X’ Y}
\end{equation} $
この式を使えば誤差の二乗和の式の第2項、第3項を一つにまとめることができます。
$ \begin{equation}
\mathbf{e’e} = \mathbf{Y’Y – 2 b’ X’Y + b’ X’ X b}
\end{equation} $
これが誤差の二乗和です。これを最小化します。1階の条件はこの式をベクトル$\mathbf{b} $ で微分してゼロと置くことで求まります。
1次形式の微分
微分は次のように計算します。$\mathbf{Y’Y}$は定数なので消去されます。$\mathbf{-2b’X’Y}$は、微分するベクトル$\mathbf{b}$を転置したものに、定数ベクトル($\mathbf{X’Y}$)を後ろ側からかけた形(1次形式)となっています。
この形の微分では一般的に$\dfrac{ \partial \mathbf{(a’x)} }{\partial \mathbf{a} }= \mathbf{x} $が成り立ちます。この場合の微分の結果は$\mathbf{-2X’Y}$となります。
2次形式の微分
また、$\mathbf{b’X’Xb}$については、$\mathbf{b}$と$\mathbf{X’X}$についての2次形式の微分が使えます。この形の微分では一般的に$\dfrac{ \partial \mathbf{(a’Xa)} }{\partial \mathbf{a} }= \mathbf{2Xa} $が成り立ちます。この場合の微分の結果は$\mathbf{2X’Xb}$です。以上の結果、次の式が成り立ちます。
$\begin{equation}
\dfrac{\partial \mathbf{e’e}}{\partial \mathbf{b }}= \mathbf{-2 X’Y + 2X’X b }=0
\end{equation}$
この式から$\mathbf{ b} $を求めることができます。
$\begin{equation}
\mathbf{b} = \mathbf{ (X’X)^{-1} X’Y }
\end{equation}$
分散共分散行列
分散共分散行列は、誤差項の各時点の分散とほかの時点との分散を計算したものです。
最小二乗法では、誤差の均一分散を仮定しています。$\mathbf e$ を残差ベクトルとすると、外積$\mathbf{ee’}$は次のように表せます。
$ \mathbf{ee’}
=\begin{pmatrix}
e_1 \\ e_2 \\ e_3 \\ \vdots \\ e_n
\end{pmatrix}=
\begin{pmatrix}
e_1 & e_2 & e_3 & \dots & e_n \end{pmatrix} \begin{pmatrix}
e_1^2 & e_1e_2 & e_1e_3 & \dots & e_1e_n \\
e_2e_1 & e_2^2 & e_2e_3 & \dots & e_2e_n \\
e_3e_1 & e_3e_2 & e_3^2 & \dots & e_2e_n \\
\vdots & \vdots & \vdots & \ddots & \vdots \\
e_n e_1 & e_Te_2 & e_Te_3 & \dots & e_n^2
\end{pmatrix}
$
$ \mathbf{ee’}$の期待値が$ \mathbf{e} $の分散共分散行列になります。均一分散を仮定しているので、$E(e_i e_j)=\sigma^2(i=j)$、$E(e_i e_j)=0(i \neq j)$ です。
$\begin{equation}
\mathbf{b} = \mathbf{ (X’X)^{-1} X’Y }
\end{equation}$
$ =E\begin{pmatrix}
e_1^2 & e_1e_2 & e_1e_3 & \dots & e_1e_n \\
e_2e_1 & e_2^2 & e_2e_3 & \dots & e_2e_n \\
e_3e_1 & e_3e_2 & e_3^2 & \dots & e_2e_n \\
\vdots & \vdots & \vdots & \ddots & \vdots \\
e_Te_1 & e_Te_2 & e_Te_3 & \dots & e_n^2 \end{pmatrix}= \begin{pmatrix}
E(e_1^2) & 0 & 0 & \dots & 0 \\
0 & E(e_2^2) & 0 & \dots & 0 \\
0 & 0 & E(e_3^2) & \dots & 0 \\
\vdots & \vdots & \vdots & \ddots & \vdots \\
0 & 0 & 0 & \dots & E(e_n^2)
\end{pmatrix} $
$ = \sigma^2
\begin{pmatrix}
1 & 0 & 0 & \dots & 0 \\
0 & 1 & 0 & \dots & 0 \\
0 & 0 & 1 & \dots & 0 \\
\vdots & \vdots & \vdots & \ddots & \vdots \\
0 & 0 & 0 & \dots & 1
\end{pmatrix}
=\sigma^2 \mathbf{I}
$
最小二乗法による係数の期待値と分散
真の係数を$\beta$、誤差を$\varepsilon$とすると真の回帰式と最小二乗法による回帰式の行列表示は次の通りになります。
$ \mathbf{ Y= \beta X + \varepsilon} (真の関係)$
$ \mathbf{ Y= b X + e } (推定による関係)$
最小二乗法による推定値 $\mathbf{ b }$ は次式です。
$ \mathbf{b= (X’X)^{-1} X’Y } $
期待値の計算
まず$\mathbf{b}$の期待値を求めます。その準備として次の変形を行います。$ \mathbf{Y}$ に真の係数と誤差の関係を代入して、$\beta$と$\varepsilon$を式の中に入れます。 $ \mathbf{A= (X’X)^{-1} X’} $ とすると、$\mathbf{b}$は次式で表されます。
$ \begin{equation}
\mathbf{b= AY = A(X \beta +\varepsilon ) = AX \beta + A \varepsilon = \beta +A \varepsilon }
\end{equation} $
$\mathbf{b}$ の期待値を計算します。$ \mathbf{A= (X’X)^{-1} X’} $ は、変数$ \mathbf{X}$をいろいろ加工したものですが、定数です。定数は、期待値計算の外に出せるので、$\varepsilon$の期待値を計算すればよいことになります。
$ E( \mathbf{b})=\beta +E (A \varepsilon )=\beta + A E( \varepsilon )=\beta $
つまり最小二乗法による推定値$\mathbf{b}$の期待値は真のパラメーターに一致し、不偏性を持つことになります。
分散の計算
次に係数の分散を求めます。期待値の計算と同様 $ \mathbf{A= (X’X)^{-1} X’}$とします。
誤差の分散($Var (\varepsilon)$ )を$\sigma^2$とすると次式に変形できます。 $\mathbf{ Var( b )= Var( A \varepsilon )}$への変形は期待値の計算と同じです。
$ \mathbf{ Var( b )= Var( \beta + A \varepsilon )=Var( A \varepsilon )=A Var( \varepsilon ) A’ = A ( \sigma ^2 I )A’ } $
$ = \mathbf{ (X’X)^{-1} X’ ( \sigma ^2 I ) ((X’X)^{-1} X’ )’ } $
転置行列や逆行列の性質($\mathbf{ (AB)’ = B’A’ }$ 、 $\mathbf{ (A’A^{-1})’ = (A’A)^{-1} }$)を使うと、次式のように変形できます。
$ \mathbf{ Var( b )}= \mathbf{ \sigma ^2 (X’X)^{-1} } $
順をおって式を追っていくと以下のようになります。
$ \mathbf{ Var( b )}= \mathbf{ (X’X)^{-1} X’ ( \sigma ^2 I ) ((X’X)^{-1} X’ )’ } $
$\mathbf{ (AB)’ = B’A’ }$ から、$ \mathbf{ ((X’X)^{-1} X’ )’ =X((X’X)^{-1})’ }$になります。$\mathbf{ (A’A^{-1})’ = (A’A)^{-1} }$から、$ \mathbf{ X((X’X)^{-1})’=X(X’X)^{-1} }$になります。
$ = \mathbf{ (X’X)^{-1} X’ ( \sigma ^2 I ) X(X’X)^{-1} } $
$\sigma^2$は定数で、どこに動かしてもいいので、最初に持ってきます。
$ = \mathbf{ \sigma^2 (X’X)^{-1} X’ X(X’X)^{-1} } $
元の行列とその逆行列の積は単位行列になるので、$ \mathbf{X’ X(X’X)^{-1}}=I $となります。
$ = \mathbf{ \sigma^2 (X’X)^{-1} } $
まとめ
行列計算による計算をまとめると以下になります。
係数は以下で表されます。
$\begin{equation}
\mathbf{b} = \mathbf{ (X’X)^{-1} X’Y }
\end{equation}$
分散共分散行列はこれです。
$\begin{equation}
\mathbf{b} =\sigma^2 \mathbf{I}
\end{equation}$
係数の期待値はこれです。
$ E( \mathbf{b})=\beta $
係数の分散はこれです。
$ \mathbf{ Var( b )}= \mathbf{ \sigma ^2 (X’X)^{-1} } $