時系列モデルの基本は、ARIMAモデルです。この記事ではARIMAモデルについてできるだけ平易に解説します。なかでもARモデルを使えば、簡単に予測値を作ることができます。
経済統計の使い方では、経済統計の入手法から分析法まで解説しています。
https://officekaisuiyoku.com/category/statistics/ARIMAモデル
時系列モデルの基本はARIMAモデルです。有馬という日本語のようですが、語源は全く違います。
ARIMAという言葉はARMAとIに分かれています。
ARはAuto Regressionの略で、自己回帰モデルと呼びます。
MAはMoving Averageの略で、移動平均モデルと呼びます。
IはintegrationのIで、差分をとることを表します。
ARIMAモデルは変数の差分をとった後で、ARMAモデルを適用することになります。
モデル一覧
まず、時系列モデルの形を眺めてみましょう。ARモデルは自分自身の過去の値を説明変数とします。MAモデルは誤差項とその過去の値を説明変数とします。
•ARモデル
$ Y_t=C+aY_{t-1} +e_t$
•MAモデル
$ Y_t=C+e_t+be_{t-1} $
•ARMAモデル
$ Y_t=C+aY_{t-1}+e_t+be_{t-1} $
•ARIMAモデル
$ \Delta(Y_t)=C+a\Delta(Y_{t-1})+e_t-be_{t-1} $
ARモデル
時系列モデルとしては、まずARモデルをマスターすることが基本です。ARモデルだけで、式を推計し、予測をすることができます。
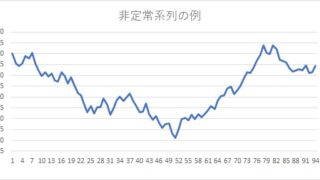
経済系列の場合は、非定常系列の場合が多いので、差分をとってからARモデルをとればよいでしょう。非定常系列の説明はこちらをご覧ください。
式としては、自分自身の過去の値を使います。
AR(1)の式は以下になります。
$ Y_t=C+aY_{t-1} +e_t $
Yt-1の値がわかれば、Ytの値が予測できます。これが基本的な予測法になります。
ラグが1の場合はAR(1)で、ラグが2の場合はAR(2)と表します。たとえばAR(3)は以下の式になります。
$ Y_t=C+aY_{t-1} +bY_{t-2}+cY_{t-3}+e_t $
MAモデル
MAモデルは、誤差項に系列相関を想定する場合です。
$ Y_t=C+e_t+be_{t-1} $
ARMAモデルは、AR項とMA項が両方ある場合です。
$ Y_t=C+aY_{t-1} +e_t+be_{t-1} $
コレログラム
ARMAモデルのラグの決定法の一つにコレログラムがあります。これは、自己相関係数と偏自己相関係数をグラフとして表したものです。自己相関係数は、当期と1期前の相関係数、当期と2期前の相関係数など、当期とn期前の変数との相関係数を表します。
自己相関係数は当期だけでなく、それまでのラグの影響を受けます。それらを取り除いた当期とn期前の変数との相関係数を表したのが偏自己相関係数です。
AR、MAの自己相関係数、偏自己相関係数は以下の特徴があります。
| 自己相関係数 | 偏自己相関係数 | |
| AR(p) | 徐々に減衰 | ラグP+1で切断 |
| MA(q) | ラグq+1で切断 | 徐々に減衰 |
| ARMA(p,q) | 徐々に減衰 | 徐々に減衰 |
Q検定
EViewsの表の場合、Q統計量はコレログラムと同じ表に載っている。「自己相関がない」という帰無仮説を仮定した場合の統計量です。p値で判断します。確率が小さければ「自己相関がない」という仮説が棄却され、確率が大きければ棄却されず、自己相関がある可能性があることになります。
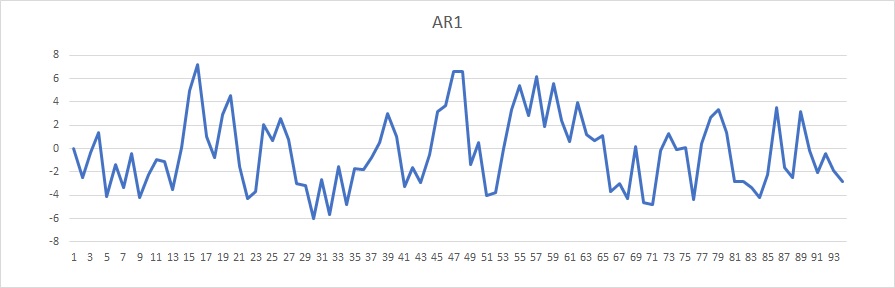
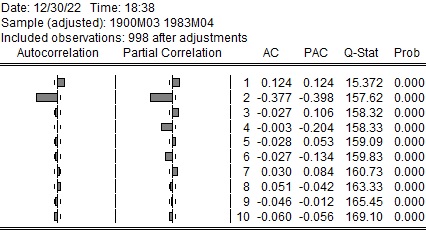
AR(1)の場合
AR(1)を人工的に作成しました。
$ Y_t=0.5Y_{t-1} +e_t $
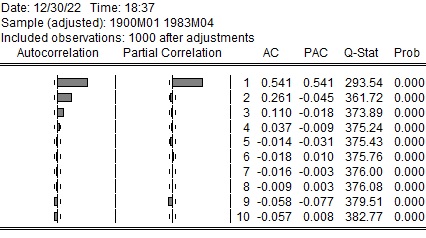
コレログラムは以下の通りになります。自己相関係数は徐々に減衰しています。偏自己相関係数は、1期目は0.541と大きいですが、その後は小さくなっていて、2期で切断されています。
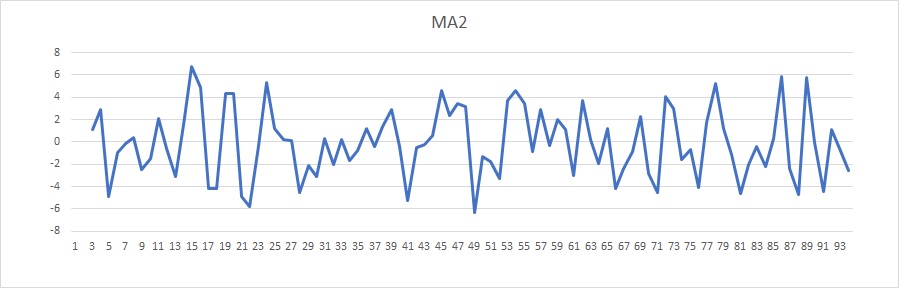
MA(2)の場合
MA(2)を人工的に作成しました。
$ Y_t=e_t+0.2e_{t-1}+0.5e_{t-2} $
コレログラムは以下の通りになります。自己相関係数は2期までは大きいですが、その後は小さく、切断されています。偏自己相関係数はプラスとマイナスを繰り返しながら徐々に小さくなっています。
推計の方法
ARモデルはエクセルで推計できます。被説明変数の1期前や2期前を説明変数にすればいいです。
しかし、MAモデルは誤差の1期前や2期前のデータを推計する必要があり、エクセルで推計することは困難です。
このため、エクセルで時系列モデル予測をする場合は、ARモデルを使ってやればよいと思います。
予測
ARMAモデルは以下の式です。
$ Y_t=C+aY_{t-1} +e_t+be_{t-1} $
1期先のYを表す式は以下の式になります。
$ Y_{t+1}=C+aY_t +e_{t+1}+be_t $
右辺の$Yt$と$e_t$は入手できる変数です。$e_{t+1}$はわかりませんが、誤差なので、平均的にはゼロになるので、ゼロを代入できます。
これを順に代入していけば、信頼区間はどんどん広がりますが、何期先までも予測できることになります。














