MCMCのソフトウエアであるStanをRで使って、単回帰分析をします。
データは、エクセルの回帰分析で使っているものと同じです。
MCMCによる単回帰分析の基本的な枠組みは、ベイズ統計です。事前に主観的な予想(事前分布)があり、新たにデータを入手することで、その主観的な分布を更新していくという仕組みです。
これらの仕組みをうまく回すためには、MCMCという手法が有効です。MCMCとは、マルコフ連鎖モンテカルロ法の略です。
経済統計の使い方では、統計データの入手法から分析法まで解説しています。

ベイズモデリング
ベイズの定理は以下で表せます。
$ P(A | B)=\cfrac{P(B | A)P(A)}{P(B)} $
最初にこれを見ても何が何だかわからないと思います。この式は、単なる恒等式です。以下の式を変形したものです。
AとBが同時に起こる確率は、Bが起った時Aが起こる確率、Aが起った時にBが起きる確率に等しいので以下の式が成り立ちます。この式の$P(B)$を移項すればベイズの定理が得られます。
$ P(A \cap B) = P(A | B)P(B)=P(B | A)P(A) $
AをデータD、Bを仮説Hとすると、以下の式になります。Hは「そのコインにはインチキがある」とか「景気は後退している」などです。
$ P(H | D)=\cfrac{P(D| H)P(H)}{P(D)} $
$P(H|D)$は、データが入手できた時のHの確率で、事後確率と呼びます。$P(H)$はデータの入手と関係ない事前確率です。$P(D|H)$は仮説を前提としてDが現れる確率で尤度、データが平均的に表れる確率は周辺尤度と呼ばれます。
さらに、仮説Hを確率分布のパラメーターθ(正規分布の場合は平均と分散)とすると、以下の式になります。確率分布のパラメータが決まるということは、確率分布が決まるということです。
$ P(θ| D)=\cfrac{P(D| θ)P(θ)}{P(D)} $
事前確率分布$P(θ)$と入手できたデータ$ P(D|θ)$を使って、事後確率分布$p(θ|D)$を作るには上の式のメカニズムを使うことになります。
ということで、データが得られれば、事後確率分布を決めることができます。問題は、その後です。θを動かしたときに確率はどう変化するかを計算するためには、事後確率分布を積分する必要があり、これが計算するうえでは難しいということです。それを解決するのが、MCMCということになります。
データ
データはエクセルの回帰分析でも使った学生の成績のデータです。
| 学生 | 基礎科目(X) | 応用科目(Y) |
| A | 50 | 60 |
| B | 55 | 55 |
| C | 45 | 60 |
| D | 55 | 65 |
| E | 65 | 60 |
| F | 65 | 70 |
| G | 75 | 75 |
| H | 75 | 80 |
| I | 80 | 90 |
| J | 85 | 85 |
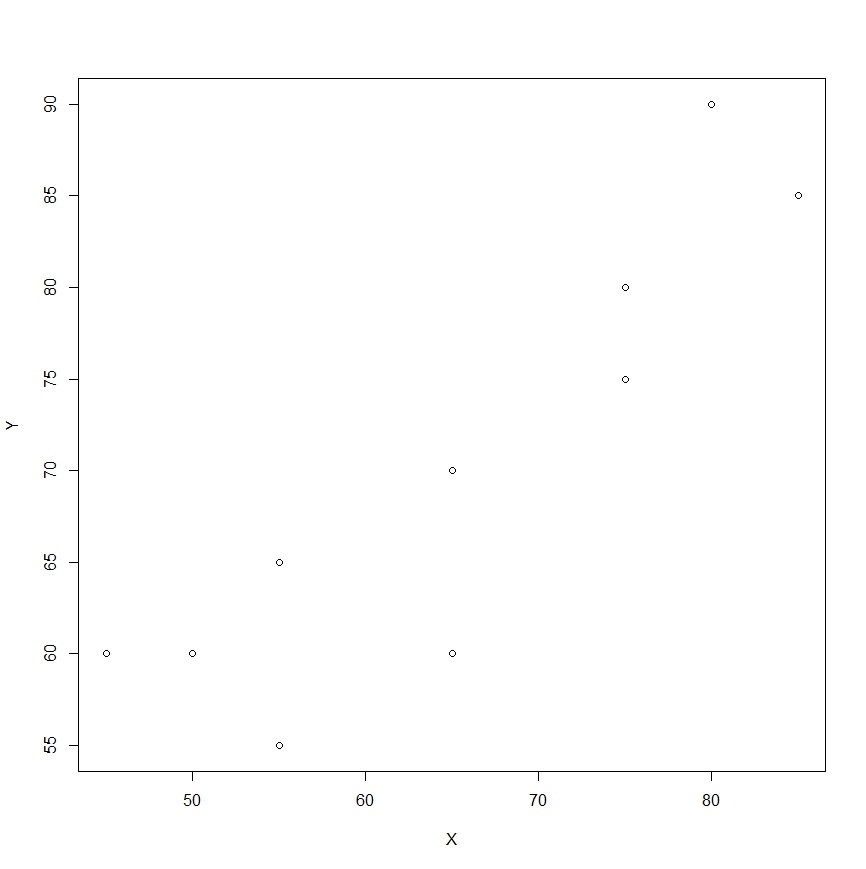
plotコマンドで散布図を描いたものです。plot(df2)です。
モデル
統計モデルとしては、線形の形を想定します。
$ Y = alpha+beta*X $
Yが正規分布に従うとすると、パラメーターは平均と標準偏差です。平均は、上式より($alpha+beta*X$)を使い、標準偏差はsigmaとします。
mcmcの結果
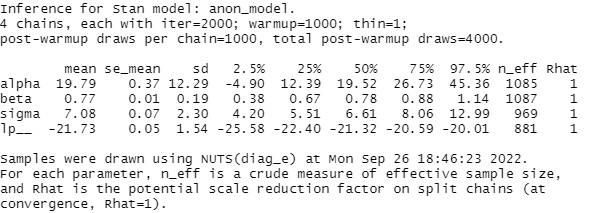
mcmcの結果は以下のようになりました。
alpphaの平均値は19.8、betaは0.77、sigmaは7.08です。
Rのプログラム
library(rstan)
library(rstudioapi)
library(bayesplot)
rstan_options(auto_write = TRUE)
options(mc.cores = parallel::detectCores())
df2 <- data.frame("X"=c(50,55,45,55,65,65,75,75,80,85),
"Y"=c(60,55,60,65,60,70,75,80,90,85))
sample_size <- nrow(df2)
sample_size
plot(df2)
data_list <- list(
N=sample_size,
Y=df2$Y,
X=df2$X
)
data_list
mcmc_result <- stan(
file = "ols.stan",
data= data_list,
seed=1
)
mcmc_result
mcmc_sample <- rstan::extract(mcmc_result, permuted = FALSE)
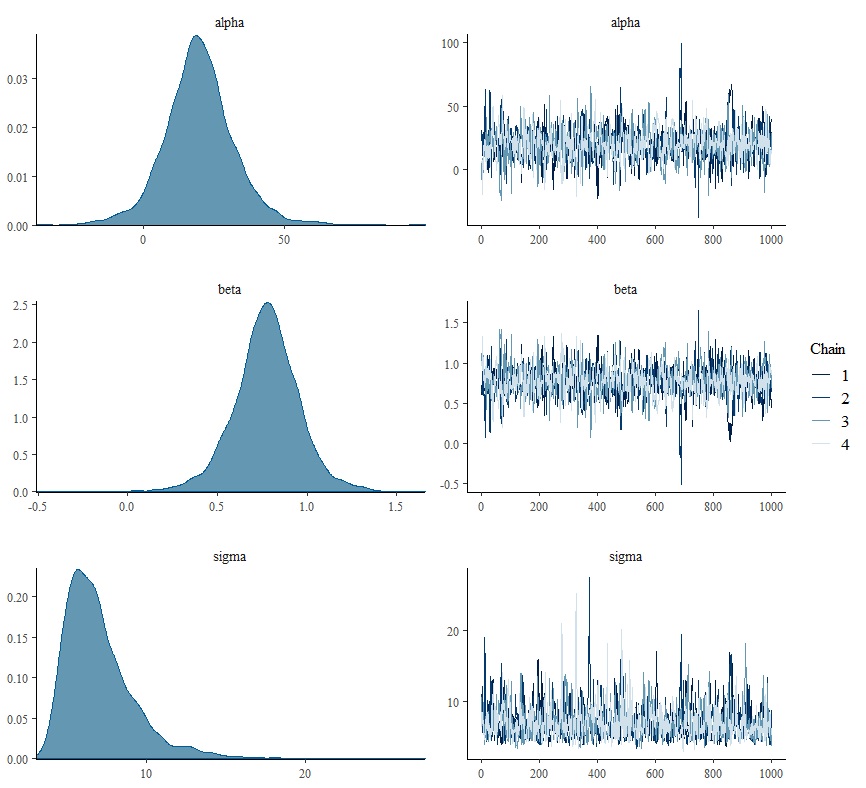
mcmc_combo(
mcmc_sample,
pars = c("alpha","beta","sigma")
)Stanのプログラム
// The input data is a vector 'Y' and 'X' of length 'N'.
data {
int<lower=0> N;
vector[N]Y;
vector[N]X;
}
// The parameters accepted by the model. Our model
// accepts two parameters 'alpha','beta' and 'sigma'.
parameters {
real alpha;
real beta;
real<lower=0> sigma;
}
// The model to be estimated. We model the output
// 'Y' to be normally distributed with mean 'alpha+beta*X'
// and standard deviation 'sigma'.
model {
Y ~ normal(alpha+beta*X, sigma);
}