2財の効用最大化問題を無差別曲線と予算線から求める問題です。通常は、計算して求めますが、エクセルを使って解いてみます。
(問)ある家計の効用関数が$ U=X_1^{(1/3)} X_2^{(2/3)} $で表されるとする。所得が120、$X_1$財の価格が1、$X_2$財の価格が4であるとき、効用最大化をもたらす最適消費量はそれぞれいくらか。【国税専門官・平成16年度】
経済統計の使い方では、統計データの入手法から分析法まで解説しています。

さまざまな組み合わせの効用を計算する
方針としては、予算上限の120で買える$X_1$と$X_2$の組み合わせを計算し、その中で効用が最大のものを選ぶということにします。
$X_1$財を0~120個買った場合について、予算内で買える$X_2$の個数を計算します。たとえば$X_1$を4個買った場合、$X_1$の価格は1なので残りは116(=120-4)です。$X_2$の価格は4なので、29(=116/4)個買えます。すべての組み合わせについて効用を計算します。べき乗は、エクセルでは^で表すので、エクセルの数式としては、X1^(1/3)*X2^(2/3)を計算します。それが以下の表です。
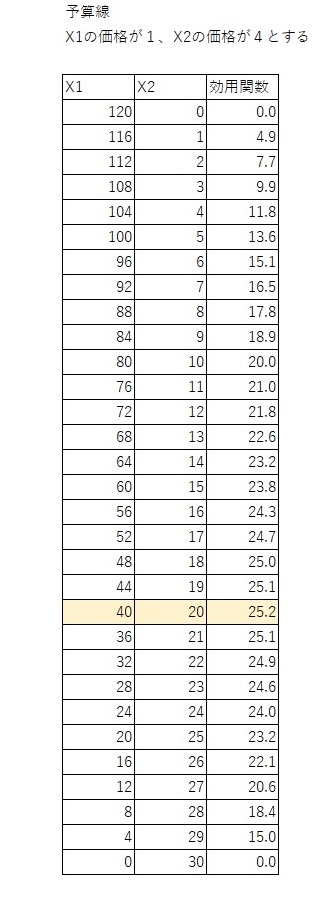
計算された効用のうち、最も高いのは$X_1$が40 個、$X_2$が20個の場合だとわかります。最大の効用は25.1984です。もちろん、$X_1$の刻み幅をもっと細かくすればさらに効用の高いところが見つかる可能性はあります。ただ、今回の場合は、計算の結果これが最大とわかっています。
無差別曲線の描画
次に、効用が最大の場合の無差別曲線を描いてみましょう。最大の効用が25.1984とわかっているので、$X_1$のそれぞれの場合について、効用が25.1984になる$X_2$を計算すればよいです。$X_2$を計算する式は以下になります。Uが左辺にある式から変形しています。
$U= X_1 ^{(1/3)} X_2^{(2/3)} $
$X_2^{(2/3)}=\frac{U}{X_1^{(1/3)}} $
$X_2=(\frac{U}{X_1^{(1/3)}}) ^{(3/2)} $
$U$は、25.1984です。$X_2$を計算すると、以下の表になります。
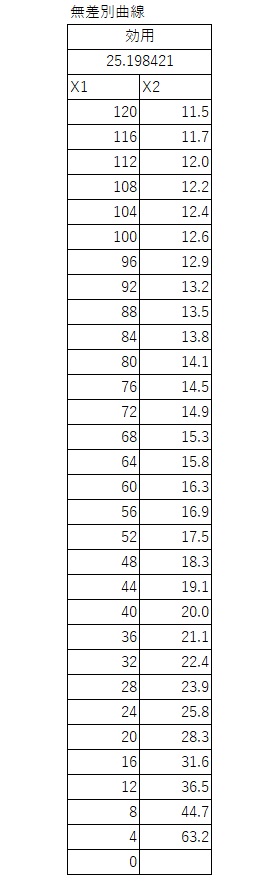
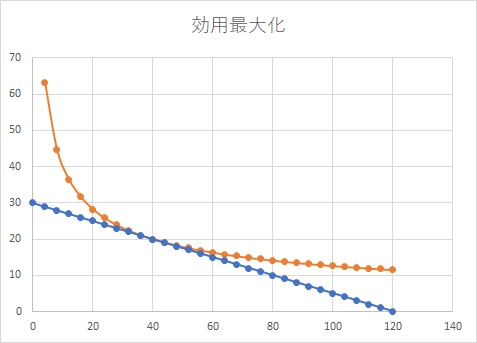
予算線と、効用が最大になる場合の無差別曲線を描くと、以下のグラフになります。