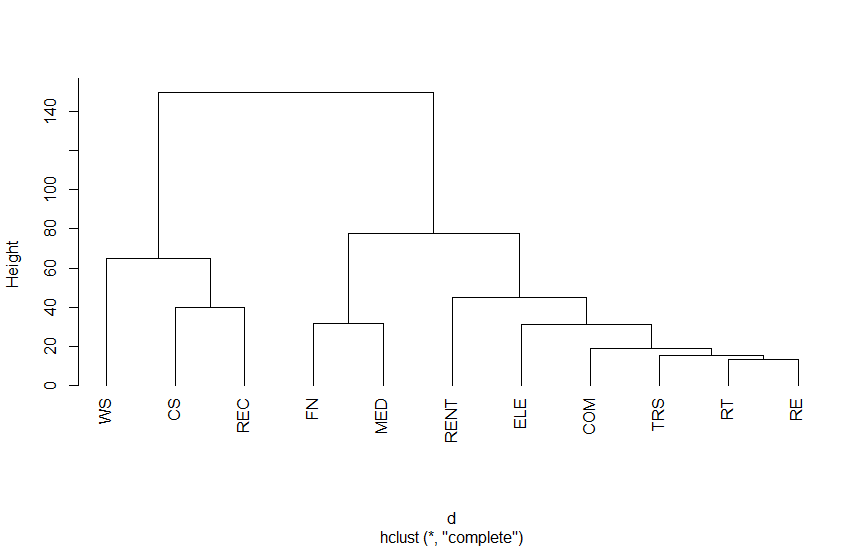
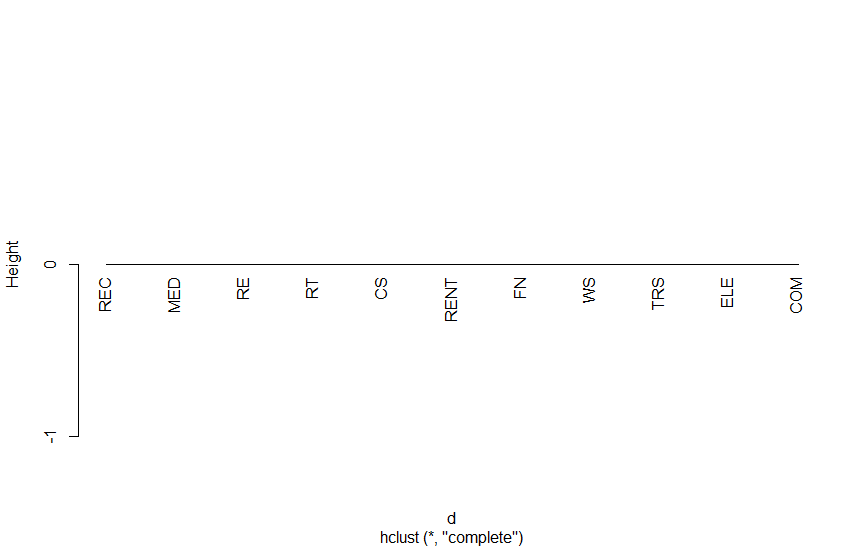クラスター分析は、類似データをまとめて、いくつかのグループ(クラスター)を作っていく手法です。変数間の距離を測り、距離の近いものから徐々にまとめていきます。距離の測り方、クラスターのまとめ方にはさまざまな方法があり、結果も変わってきます。距離については、ユークリッド距離、まとめ方についてはウォード法を選べばよいと思いますが、分析目的などによっては方法を変える必要があると思います。
経済統計の使い方では、統計データの入手法から分析法まで解説しています。

クラスター分析とは
クラスター分析は、類似データをまとめて、いくつかのグループにするものです。いくつのグループにするかは決まりはなく、分析者が決める必要があります。
クラスター分析のうち、階層型クラスター分析は、似ているものから順にまとめていく手法です。似ているかどうかの判断には距離を使います。手順としては以下になります。
- すべての組み合わせの距離を計算し、最も距離の近いもの2つを1つのクラスターにする。
- 2番目に距離に近いデータについて、他のデータとクラスターにするか既存のクラスターに含めるかを判断する
こうした判断を繰り返して、クラスターを作成していきます。
階層型クラスター分析と非階層型クラスター分析
階層型クラスター分析はデータの距離を総当たりで調べるので、データ数が多いと計算量が増えます。データ数が多い場合は非階層型クラスター分析を使います。
2つのデータの距離の測り方
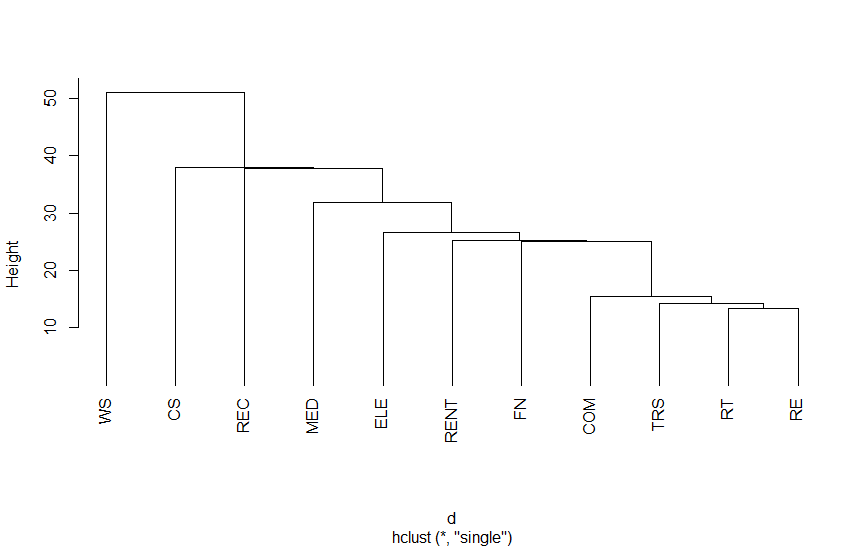
2つのデータの距離の測り方には以下のものがあります。距離の測り方で分類結果が微妙に変わります(付表参照)。手順に最初は、「最も近いものを1つにする」ということですが、距離の測り方が違うことで、最初に作られるグループが変わることがあります。相関係数の計算法と似ているのはユークリッド距離なので、経済分析ではユークリッド距離を使えばよいのではないかと思います。
| 距離の種類 | dist関数で指定できる距離 |
| euclidean | ユークリッド距離 |
| maximum | 最大距離(シェビチェフ距離) |
| manhttan | マンハッタン距離 |
| canberra | キャンベラ距離 |
| binary | バイナリー距離 |
| minkowski | ミンコフスキー距離 |
$$ ( \sum_{n=1}^p | X_k – Y_k |^m ) ^{\frac{1}{m}} $$
上記式で、m=1の場合がマンハッタン距離、2の場合がユークリッド距離、∞の場合が最長距離となります。ミンコフスキー距離はその一般型です。
バイナリー距離はゼロと1で表された画像データなどの距離を表す場合に使うようです。経済データの場合は距離がすべてゼロになるので使えません。
変数の結合法
クラスターを結合する方法には、さまざまな方法があります。
ウォード法は、最小分散法とも呼ばれ、分散に注目してグループ間の分散を最大化するようにクラスターを作っていくものです。
そのほかは、距離を基準にしていますが、クラスター間の距離の測り方が違います。
| 結合法の種類 | クラスタ-作成の基準 | hclust関数、methodの引数 |
| 最短一致法 | 最も近い個体間の距離 | single |
| 最長一致法(デフォルト) | 最も遠い個体間の距離 | complete |
| 群平均法 | 個体間の距離の平均 | average |
| メディアン法 | 重心法の変形 | median |
| ウォード法 | グループ間の分散を最大化 | ward.D2 |
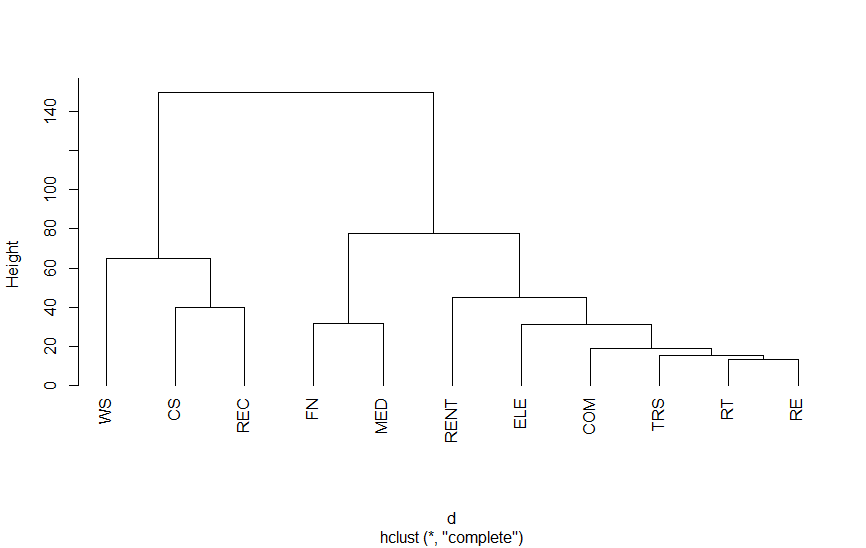
以下は、第3次産業活動指数の業種別指数をクラスター分析を適用したものです。結果をみていただければわかりますが、さまざまな分類法があります。
| 業種 | 略号 | 業種 | 略号 |
| 電気・ガス・熱供給・水道業 | ELE | 事業者向け関連サービス | CS |
| 情報通信業 | COM | 小売業 | RT |
| 運輸業,郵便業 | TRS | 不動産業 | RE |
| 卸売業 | WS | 医療,福祉 | MED |
| 金融業,保険業 | FN | 生活娯楽関連サービス | REC |
| 物品賃貸業(自動車賃貸業を含む) | RENT |
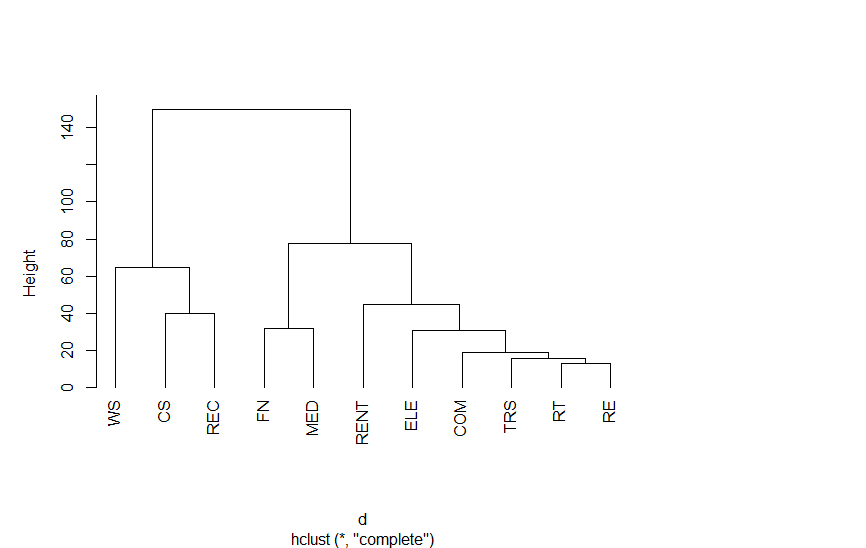

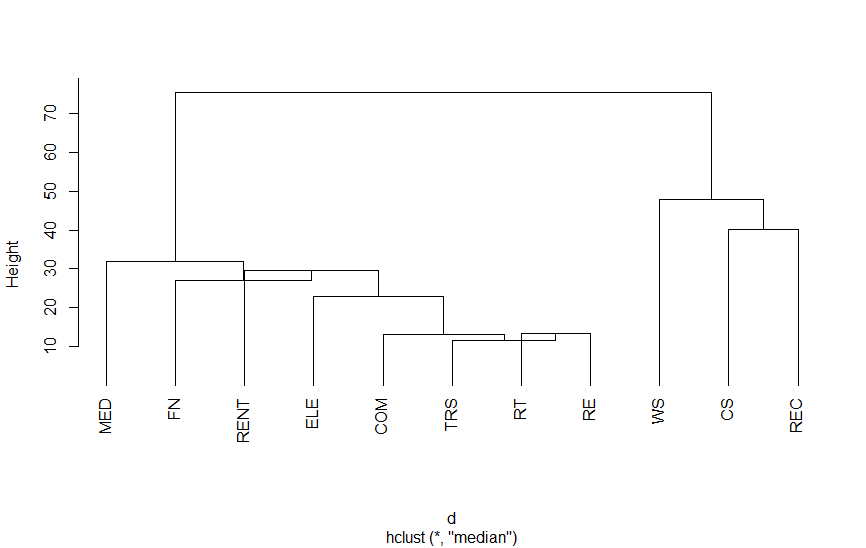
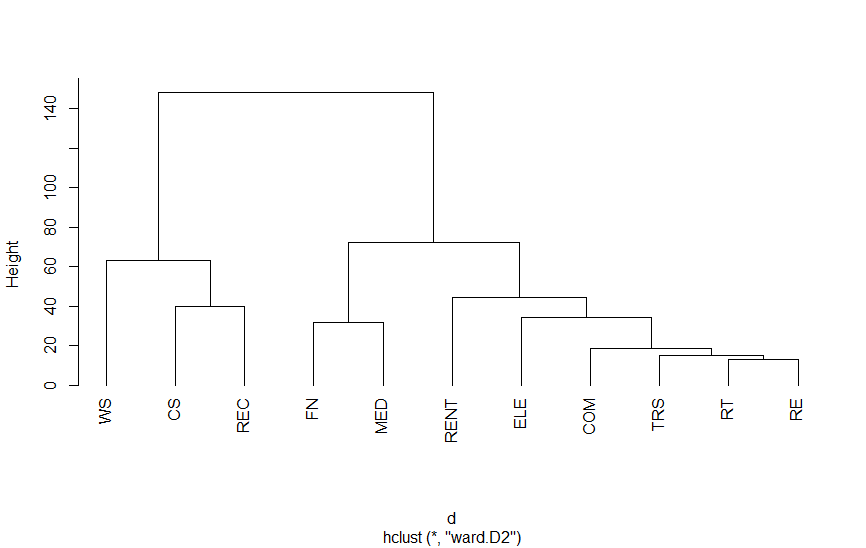
Rのプログラム
クラスター分析に必要なコマンドは、dist関数とhclust関数です。
dist(データ、method=”測る方法”)
dist関数で距離の測り方を決めます。プログラムではユークリッド距離を選んでいます(method=”euclidean”)。
dist関数で距離は行ごとに測ります。データフレームの変数は列ごとに並んでいるので、t()で行列を転置しています。
hclust(距離データ,method=”クラスターを作る方法”)
hclust関数でクラスター分析が実行されます。hclust(d,method= “complete”)のdはdist関数によって計算された距離を指定します。
tai2022<- fread("tai2022.csv",header=TRUE,data.table=FALSE,stringsAsFactors = TRUE)
tai <- tai2022[,3:13]
d <- dist(t(tai),method="euclidean")
print(d,digit=2)
hc <- hclust(d,method= "complete")
hc
plot(hc,hang=-1,main=NA)付表 距離の測り方による結果の違い