【計量経済学】決定係数｜当てはまりを表すものさし

経済統計の使い方では、統計データの入手法から分析法まで解説しています。

統計学・計量経済学のまとめ 統計学に関するまとめのサイトです。 教科書 「回帰分析から学ぶ計量経済学－Excelで読み解く経済の仕組み」 回帰分...

どの程度当てはまっているかを表す

決定係数は、回帰式を推定したときに、どの程度データに当てはまっているのかを示します。決定係数を説明する場合、全変動というあまり使わない用語が出てきますが、まずは、

実績値と理論値の相関を表すもの

と考えるのが良いのではないかと思います。詳しく言うと、「実績値と理論値の相関係数を二乗したもの」です。相関係数に関してはこちらを参考にしてください。

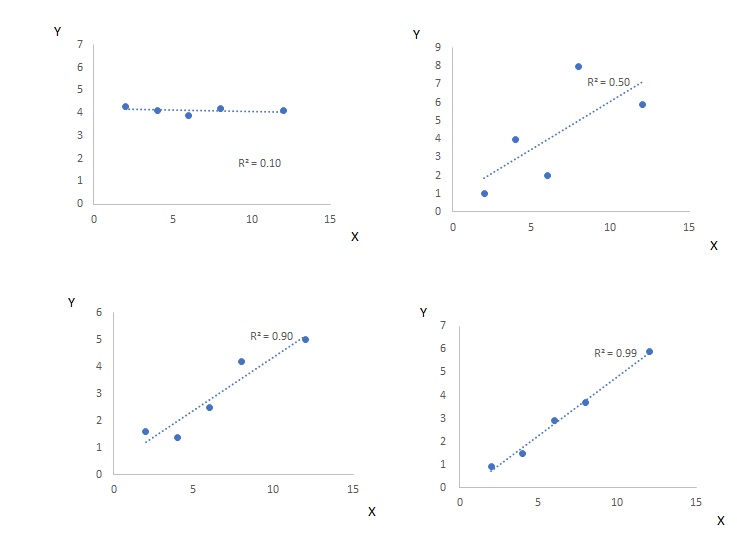
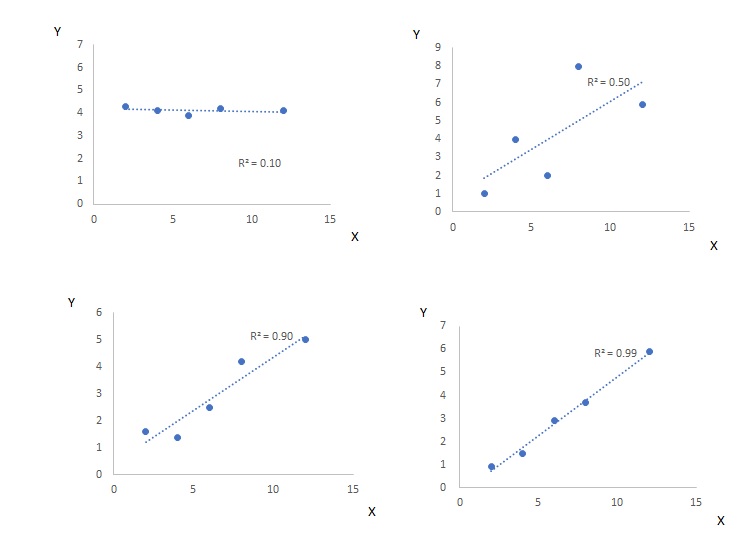
このため、０が全く当てはまってない場合、１は実績と理論値が残差なくぴったり会ったものを表します。決定係数が0.10、0.50、0.90、0.99のばらつき具合は以下の図の通りです。決定係数が0.10の場合は直線は当てはまっているように見えますが、Xが動いてもYはほとんど変化せず、ほとんど定数項だけで説明していることになっています。

実績値($Y_i$)と理論値($\widehat{Y_i}$)と残差($u_i$)は以下の関係にあります。

$Y_i=\widehat{Y_i}+u_i$

実績値が理論値とどのくらい合っているかを考えるわけですが、両者の平均をとっても意味がありません。最小二乗法では実績値と理論値の平均は同じで、誤差の平均はゼロになるためです。

そこで、実績値と理論値の相関を考えます。以下の式は、実績値と理論値の相関係数の二乗を表しています。$\overline{Y}$は$Y_i$の平均です。

$\mathrm{実}\mathrm{績}\mathrm{値}\mathrm{と}\mathrm{理}\mathrm{論}\mathrm{値}\mathrm{の}\mathrm{相}\mathrm{関}\mathrm{係}\mathrm{数}\mathrm{の}\mathrm{二}\mathrm{乗}$

$=\frac{\mathrm{実}\mathrm{績}\mathrm{値}\mathrm{と}\mathrm{理}\mathrm{論}\mathrm{値}\mathrm{の}\mathrm{共}\mathrm{分}\mathrm{散}\mathrm{の}\mathrm{二}\mathrm{乗}}{\mathrm{実}\mathrm{績}\mathrm{値}\mathrm{の}\mathrm{分}\mathrm{散}\times \mathrm{理}\mathrm{論}\mathrm{値}\mathrm{の}\mathrm{分}\mathrm{散}}$

$\frac{(\mathrm{\Sigma }(Y_i-\overline{Y_i})(\widehat{Y_i}-\overline{Y}){)}^2}{\mathrm{\Sigma }(Y_i-\overline{Y}{)}^2\mathrm{\Sigma }(\widehat{Y_i}-\overline{Y}{)}^2}$

これを変形すると以下の式になります。これが決定係数の定義として使われるものです。

$\mathrm{決}\mathrm{定}\mathrm{係}\mathrm{数}＝{\displaystyle \frac{\mathrm{\Sigma }(\widehat{Y_i}-\overline{Y}{)}^2}{\mathrm{\Sigma }(Y_i-\overline{Y}{)}^2}}$

分母の$\mathrm{\Sigma }(Y_i-\overline{Y}{)}^2$は実績値の平均からの偏差の二乗和で全変動と呼ばれます。実績値の分散を計算する際の分子です。分子の$\mathrm{\Sigma }(\widehat{Y_i}-\overline{Y}{)}^2$は回帰変動と呼ばれ、回帰式によって説明された部分になります。回帰変動によって説明できなかった部分が残差変動になり、以下の式が成り立ちます。

$\mathrm{全}\mathrm{変}\mathrm{動}＝\mathrm{回}\mathrm{帰}\mathrm{変}\mathrm{動}\text{+}\mathrm{残}\mathrm{差}\mathrm{変}\mathrm{動}$

全変動、回帰変動、残差変動をまとめると以下になります。

$\mathrm{全}\mathrm{変}\mathrm{動}=\mathrm{\Sigma }(Y_i-\overline{Y}{)}^2$

$\mathrm{回}\mathrm{帰}\mathrm{変}\mathrm{動}＝\mathrm{\Sigma }(\widehat{Y_i}-\overline{Y}{)}^2$

$\mathrm{残}\mathrm{差}\mathrm{変}\mathrm{動}＝\mathrm{\Sigma }(Y_i-\widehat{Y_i}{)}^2$

決定係数は以下のようにも書き換えられます。

$\mathrm{決}\mathrm{定}\mathrm{係}\mathrm{数}={\displaystyle \frac{\mathrm{回}\mathrm{帰}\mathrm{変}\mathrm{動}}{\mathrm{全}\mathrm{変}\mathrm{動}}}=1-{\displaystyle \frac{\mathrm{残}\mathrm{差}\mathrm{変}\mathrm{動}}{\mathrm{全}\mathrm{変}\mathrm{動}}}$

自由度修正済み決定係数

決定係数は、当てはまりを示す指標なので、説明変数を増やせば増やすほど、多かれ少なかれ決定係数は上昇します。説明変数が増えることで、係数の数値を低めるようにしたものが自由度修正済み決定係数です。残差二乗和をRSS、全変動をＴＳＳ、サンプル数をｎ、定数項を含む説明変数の数をＫとすると以下の式になります。

$\mathrm{自}\mathrm{由}\mathrm{度}\mathrm{決}\mathrm{定}\mathrm{済}\mathrm{み}\mathrm{決}\mathrm{定}\mathrm{係}\mathrm{数}＝1-{\displaystyle \frac{RSS/(n-K)}{TSS/(n-1)}}$

RSSの関数ととらえる

残差変動は、残差二乗和（RSS：Residual Sum of Squares）と同じです。

当てはまりの指標という意味では、RSSがどの程度小さいか、という方向から考えることもできます。AICなどそのほかの当てはまり指標も基本的にはRSSの関数です。TSSを全変動、nをサンプル数、Kを定数項を含めた説明変数の数とすると、以下の式となります。

決定係数

$R^2=1-{\displaystyle \frac{RSS}{TSS}}$

対数尤度

$lnL=-{\displaystyle \frac{n}{2}}(1+\log 2\pi +{\displaystyle \frac{\log RSS}{n}})$

赤池情報規準(AIC)

$AIC=\log ({\displaystyle \frac{RSS}{n}})\mathrm{を}+{\displaystyle \frac{2K}{n}}$

シュワルツベイズ情報規準（SBIC)

$SBIC=\log ({\displaystyle \frac{RSS}{n}})+\log n{\displaystyle \frac{K}{n}}$

8種類算出法がある！

決定係数には8種類の算出法があり、統計ソフトによって異なる方法を使っている場合があります。Kvalseth(1985)には、8種類の決定係数の計算法が紹介されています。基本的には１式や２式で計算するわけですが、定数項が無い場合の回帰や非線形回帰の場合にほかの計算法が使われます。

ただ、線形回帰で、定数項がある場合は（１）式（２）式で問題ないので、通常はそれほど気にしなくてもよいでしょう。この記事で最初に紹介したのは（６）式です。

• 【python】 クラスとインスタンス
• 【python】関数の作成
• AI関連の分析ツールの紹介ーー生成AIなど
• 【Python】Pythonの基本操作
• 経済学Q＆A（試験編）

検索

検索