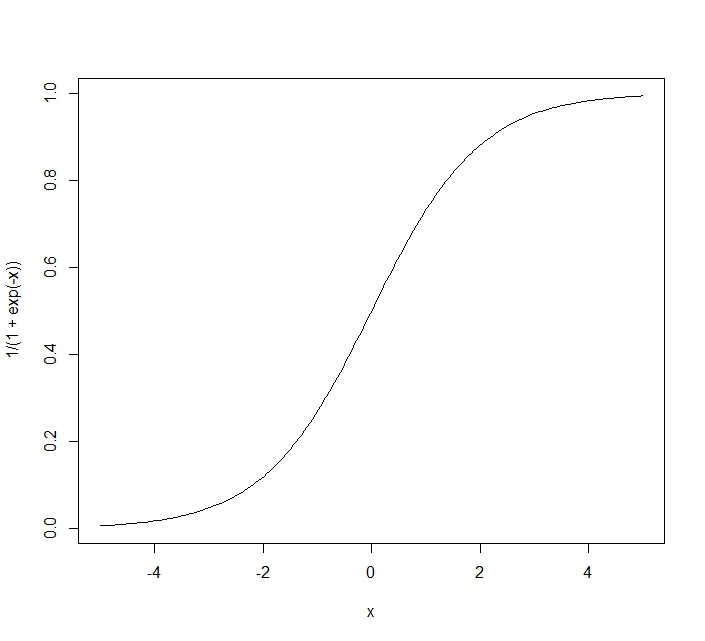
ロジスティック曲線は、家電の普及率など徐々に増え方が小さくなって、ある飽和点がある曲線です。
ロジスティック回帰は、普及率や成長の予測をするときに使い、式を変形すると最小二乗法で推定できます。
ロジットは、被説明変数がゼロか1の場合に使う推計法です。普通の最小二乗法で推計すると当てはまりが悪いので、推定値がロジスティック曲線に沿うように係数を推定するものです。
経済統計の使い方では、統計データの入手法から分析法まで解説しています。

ロジスティック曲線とは
最も単純なロジスティック曲線は以下の式で表されます。
$ f(x)=\dfrac{1}{1+e^{-x}} $
- $x$が負の時、$e$の肩ににかかる係数はプラスになるので$x$が小さいほど大きくなります。分母がどんどん大きくなるので、$f(x)$はゼロに近づきます。
- $x$がゼロの時、$ \dfrac{1}{1+1}=0.5 $になります。
- $x$が正の時 $e$の肩にかかる係数はマイナスになり、$x$が大きいほど小さくなります。分母はどんどん1に近づくので、$f(x)$も1に近づきます。
上記は飽和点(それ以上増えない点)が1の場合ですが、飽和点をSとすれば、以下の式になります。
$ f(x)=\dfrac{S}{1+e^{-x}} $
被説明変数がロジスティック曲線に従う場合は、これを使って予測することができます。
$ Y=\dfrac{S}{1+e^{-X}} $
$ -log(\dfrac{S-Y}{Y})=\alpha + \beta X $
$ Z=-log(\dfrac{S-Y}{Y}) $とすると、以下の式を推計すればよいことになります。
$ Z=\alpha + \beta X $
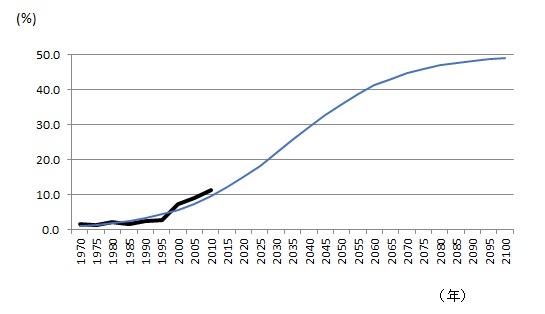
グラフは、小巻・山澤『計量経済学15講』で使ったもので、国会議員の女性比率がロジスティック曲線に沿って増えるとどうなるかを予測したものです。
ロジット
被説明変数が、就職しているかどうか、日本人かどうかなど、1か0で表されるような場合を、質的従属変数と呼びます。この場合、通常の最小二乗法を使うとうまく推計できません。
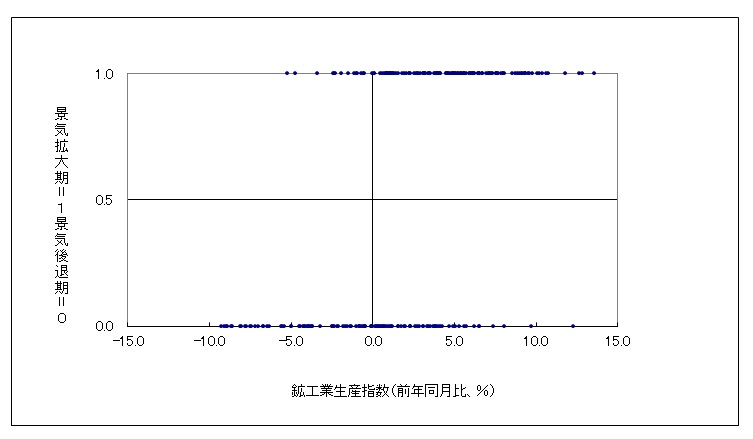
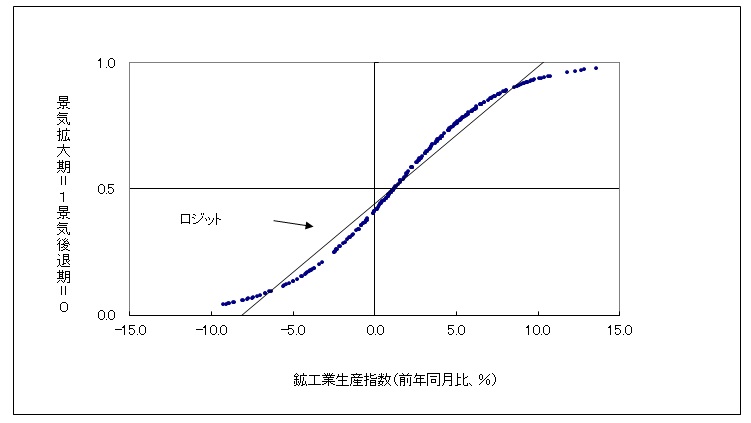
たとえば、縦軸を景気が良い場合を1,悪い場合を0、横軸は鉱工業生産指数の前年同月比伸び率でグラフを描くと以下のようになります。山澤『実戦計量経済学入門』の例でサンプル期間は1980年1月から2000年12月です。
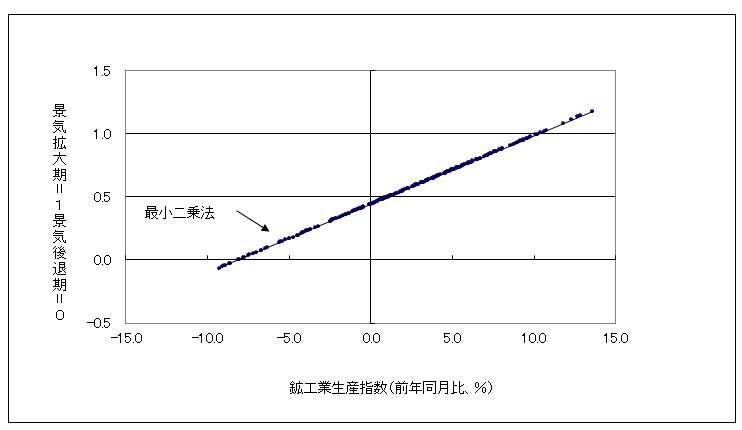
これを最小二乗法で推定すると、以下のグラフになります。推定値がゼロ未満や1を超えているものがあります。
ロジットで推計したものが以下です。鉱工業生産指数の伸び率をロジスティック曲線に沿うように変換したもので、推定値はゼロから1の間に収まります。景気の様子を連続的に表すことができるようになります。
ロジスティック曲線のグラフ
ロジスティック曲線を理解するため、Xからどのようにグラフが変化するか見てみましょう。-5から5の範囲で200個のXを作ります。
Xのグラフ
x<-seq(-5,5,length=200)
plot(x,x,type="l")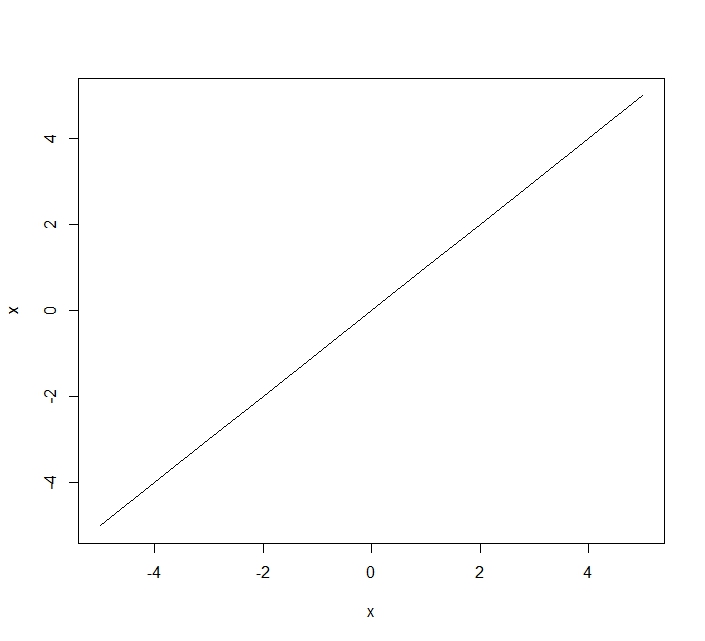
指数関数のグラフ($e^{-x}$)
x<-seq(-5,5,length=200)
plot(x,exp(-x),type="l")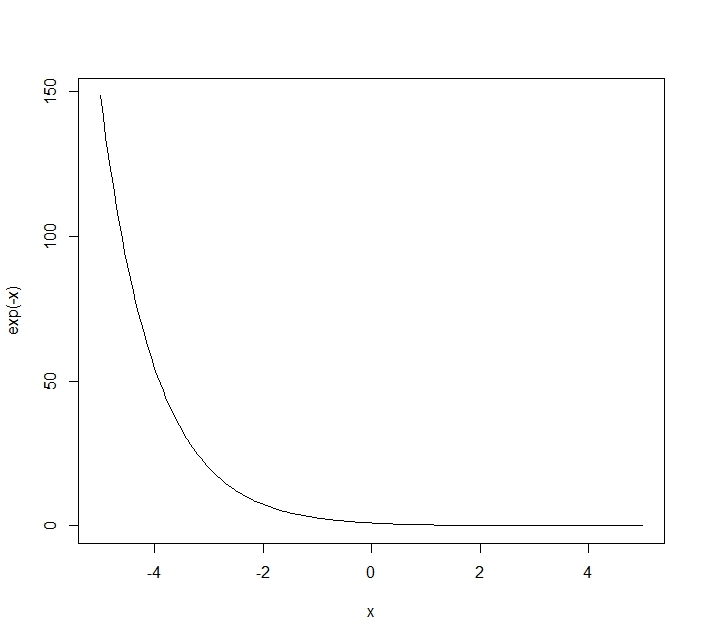
指数関数に1を加えるグラフ $(1+e^{-x})$
x<-seq(-5,5,length=200)
plot(x,1+exp(-x),type="l")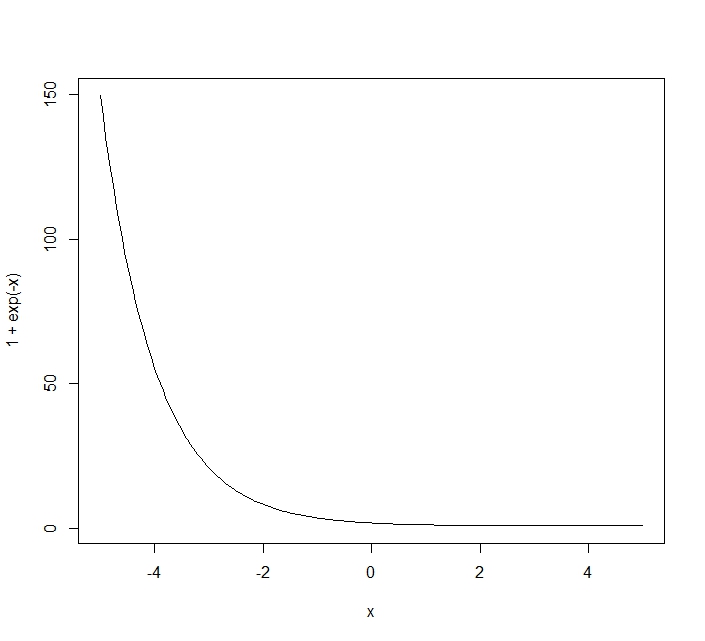
逆数をとるとロジスティック曲線($\dfrac{1}{1+e^{-x}}$)
x<-seq(-5,5,length=200)
plot(x,1/(1+exp(-x)),type="l")