【経済学】米国金利上昇による円安｜円安はどこで止まるか？（アセットアプローチ）

「米国金利が上昇すると円安になる」とよく聞きます。米国に預けた方が利子が高いので、ドルへの需要が高まるからドル高・円安になる、と説明されることが多いです。そうるすと、永遠にドルへ資金が流れる気がしませんか？

なぜドルへの資金流出は止まるのでしょか。円安になるとして、どの程度円安になるのでしょうか？為替レート決定理論の一つ、アセットアプローチを使うと、どの程度円安になるかが計算できます。

経済統計の使い方では、統計データの入手法から分析法まで解説しています。

【経済学】経済学のまとめ経済学の基本的な考え方について説明しました。経済統計の使い方では、統計データの入手法から分析法まで解説しています。 ...

Contents

アセットアプローチ
日米金利が等しい場合
米国金利が上昇したら
金利平価条件
リスクプレミアムを考慮した場合

アセットアプローチ

アセットアプローチは、資産（アセット）の最適化が為替レートを決定するという理論です。長期的な為替レートの決定理論として購買力平価がありますが、アセットアプローチは短期的な為替レート決定理論で、均衡為替レートは金利平価と呼ばれます。

【経済統計】購買力平価からみた為替レートー長期的な水準の目安｜ビッグマック指数も紹介さくら円安が進んでいますが、どの程度が適当な水準何でしょうかかえで購買力平価が1つの目安になります。経済統計の...

日米金利が等しい場合

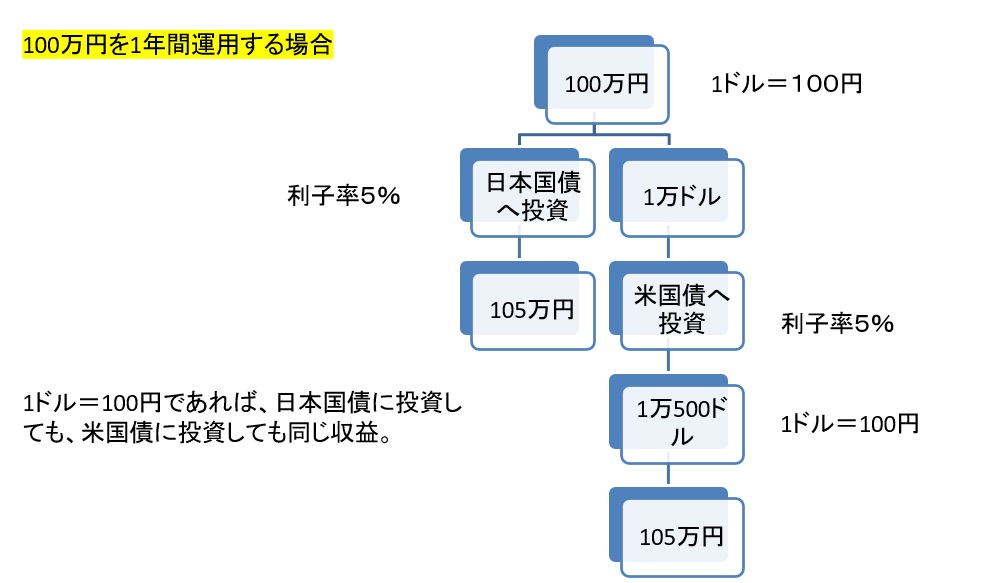
まず、日米金利が等しい場合を考えます。100万円を持っていて1年間運用する場合です。日本国債の利子率が５％の時、1年後には105万円を入手できます。

米国債で投資するとして、為替レートが現在も1年後も1ドル＝100円だとします。まず、100万円をドルに換えます。1ドル＝100円の場合、1万ドルになります。利子率が５％の場合、1年の投資で５％増えて、1万500ドルになります。それを円に換えると105万円になります。

日本で運用しても米国で運用しても同じ収益率が得られることになります。

米国金利が上昇したら

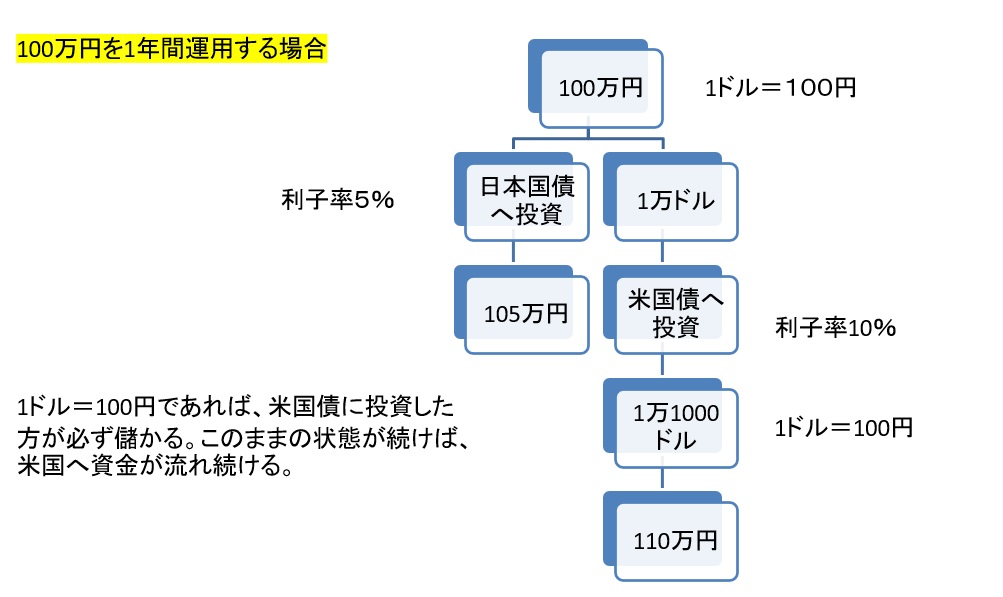
米国の金利が上昇したらどうなるでしょう。

日本国債へ投資した場合は、1年後に105万円が入手できます。

米国金利が10％に上がった場合、1年後には1万1000ドル入手でき、為替レートが変わらない場合110万円が手に入ります。

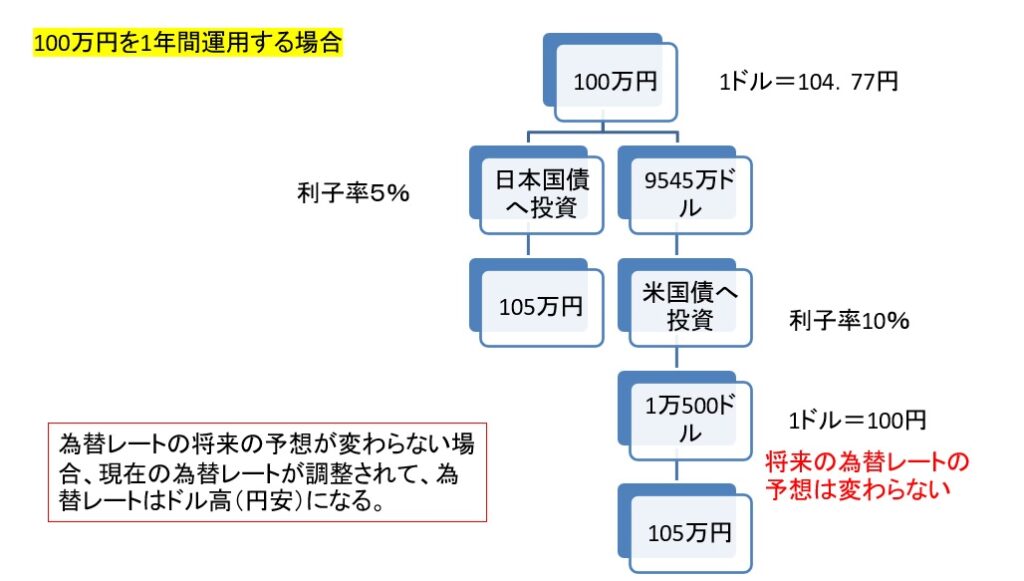
しかし、永遠に米国に資金が流れ続けるわけではありません。将来の為替レートの予想が変わらない場合、現在の為替レートが動いて、収益が同じになるように調整されます。

米国債に投資しても同じ収益率をえることができるようになるには、為替レートが1ドル＝100円から、1ドル＝104.77円へと円安になる必要があります。

つまり米国の金利上昇は、ドル高・円安をもたらしますが、日本と米国での収益率が同じになったところで円安は止まります。

金利平価条件

上で例示した日本国債と米国債の選択について、式で表していきます。

現在の為替レート（円建て）を$e_t$、1年後の予想為替レートを$e_{t+1}　$とすると、為替レートの収益率は以下の式になります。

$ \dfrac{e_{t+1}-e_t}{e_t} $

例えば、1ドル＝100円が1ドル＝110円になると、100円だったものが110円になるので、収益率は10％となります。

日本国債の利子率を$r$、米国債の利子率を$r’$とします。$m$円持っているとすると、国内で運用した場合の収益率は$r$です。

米国で運用した場合の収益率は、ドルへの変換があるので、多少面倒です。$m$円をドルに換え（$\frac{m}{e_t} $）、それに金利をかけることで、1年後の受取額($ \frac{m}{e_t}*(1+r’) $)が計算できます。それを円に換えたものが円建ての受取額($\frac{m}{e_t}*(1+r’)*e_{t+1} $)です。受取額から$m$を引いて収益額とし、収益額を$m$で割って収益率としたものです。

$ \dfrac{\frac{m}{e_t}*(1+r’)*e_{t+1} -m }{m}$

$=\dfrac{(1+r’)e_{t+1}}{e_t}-1$

この式をさらに展開すると、以下の式になります。

$ \dfrac{(1+r’)e_{t+1}}{e_t}-1　$

$= \dfrac{(1+r’)e_{t+1}-e_t}{e_t}$

$=r’+\dfrac{e_{t+1}-e_t}{e_t} +\color{red}\dfrac{r'(e_{t+1}-e_t)}{e_t} $

第3項は比率に比率をかけたもので、かなり小さいため無視すると、日本国債の収益率と米国債への投資の収益率は等しくなるはずなので、以下の近似式が成りたちます。これを金利平価条件と呼びます。

$ r \fallingdotseq r’+\dfrac{e_{t+1}-e_t}{e_t} $

$ 日本国債の円建ての収益率　\fallingdotseq　米国債のドル建て収益率+為替レートの予想収益率 $

上の例では以下の式で、現在の為替レートを導きだせます。

$ 0.05　\fallingdotseq　\dfrac{100-e_t}{e_t}+0.1 $

計算すると、1ドル＝105.26円となります。収益率での計算は第3項を無視しているので、近似的な計算となり、上記の例の結果（1ドル＝104.77円）とは異なります。

近似式は、金利が低い時にはそれほど差が生まれませんが、今回の例のように５％、10％といった高さだと、差が大きくなります。

リスクプレミアムを考慮した場合

リスクプレミアムとは、利益が確定しているものへの投資に比べてリスクのあるものへの投資の収益率には割増収益（プレミアム）があるはずだ、という考え方です。

日本国債に投資する場合は確実に利子が得られますが、米国債に投資した場合は、将来の為替レート次第で収益額が変わります。円安になって大儲けできる場合もあれば、円高になって損をする場合もあります。リスクを取る分、上記金利平価条件で得られる収益率にさらに利益が割り増しされなければ投資家は投資しないと考えるわけです。

リスクプレミアムを考慮した金利平価条件は以下の式となります。

$ 日本国債の円建ての収益率+リスクプレミアム=米国債のドル建て収益率+為替レートの予想収益率 $

上記と同じ例で、リスクプレミアムを３％とすると、以下の式となります。

$ 0.05+0.03　\fallingdotseq　\dfrac{100-e_t}{e_t}+0.1 $

この場合の現在の為替レートは1ドル＝102.04円となります。