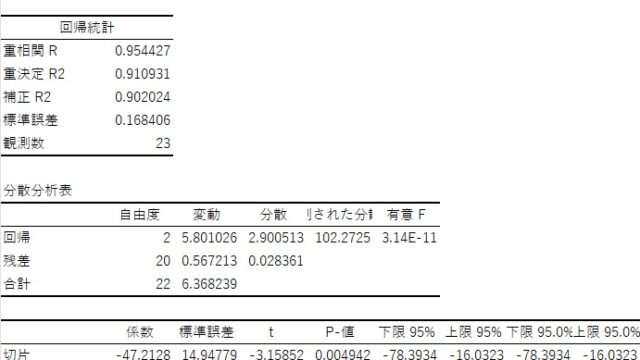
pythonで自己回帰モデルの予測をしてみます。statsmodels.tsa.ar_modelモジュールの中のAutoRegというクラスを使い、以下の式で計算できます。
AutoReg(データ,lag=ラグ数)
このモデルの計算結果はfitメソッドでモデルを訓練できます。この結果を使って、結果の確認、係数の出力や予測などができます。
経済統計の使い方では、経済統計の入手法から分析法まで解説しています。

データは、以下のデータを使います。景気動向指数のデータです。
import pandas as pd
df=pd.read_csv("CI.csv")
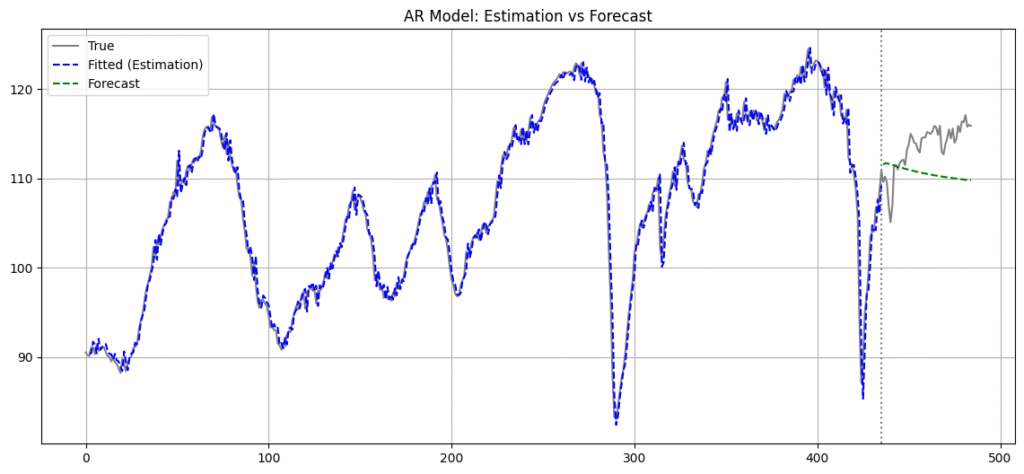
df.head()景気動向指数のデータです。灰色の線が実績値、青がサンプル内の推定値、緑が予測値となっています。
自己回帰モデル
自己回帰モデルは、自分自身に回帰するもので、基本的な予測を作成する方法の一つです。ラグ数が1で、定数項をa,CIの係数をbとして以下の式を推計することになります。
$ CI_t=a+b CI_{t-1} $
自己回帰モデルの核となる式は以下です。
AutoReg(データ,lag=ラグ数)
このモデルを使って係数を推定する場合は、fitメソッドを使います。
model=AutoReg(データ,lag=ラグ数).fit()
fitメソッドの結果をmodelという名前にして保存しています(resultsなどの名前でもいいです)。modelはAutoRegResultsというクラスのインスタンスとして保存されるので、AutoRegResultsのメソッドを使うことができます。さまざまな推定結果が保存されています。
| summary() | 結果 |
| fittedvalues | 推定 |
| predict(予測初期、予測終期) | 予測 |
| params | 係数 |
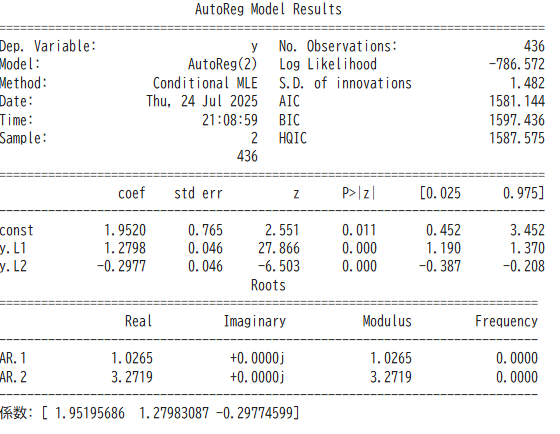
以下は結果の表示です。
サンプル数の調整
自己回帰モデルは、自分自身の過去の値を使うので、たとえばラグが2期の場合、推定できるのは3番目からのデータになります。3つのサンプルがあったとしても、使えるのは3-2=1サンプルです。サンプル数(sample_size)はデータの個数-ラグ数となります。
学習データをサンプル数の90%とすると、サンプル数×0.9で学習データ数(train_size)が求められます。これをもとのデータから切り出す場合、データ初期はゼロです(サンプルサイズはラグ数分減ります)。学習データの終期は以下の表から、train_size-1+ラグ数となり、スライス記法では1期先を指定するので、train_size+ラグ数となります終
予測期間は、学習期間の終わりから1期後なので、train_size-1となります。終期は最後のデータのインデックス(ゼロから始まる)を指すので、データ数(len()で取得できます)-1となります。
- 学習期間:(スライス記法)配列名[:train_size+ラグ数]
- 検証期間:予測初期はtrain_size+ラグ数,終了期はデータ数-1
| インデックス | サンプル数(ラグが2の場合) | インデックスが2の時の変数 |
| 0 | $X_{t-2}$ | |
| 1 | $X_{t-1}$ | |
| 2 | 1 | $X_t$ |
| 3 | 2 | $X_{t+1}$ |
| : | : | |
| train_size-1+ラグ数 | train_size | ←学習期間の終期 |
| train_size+ラグ数 | : | ←検証期間の初期 |
| : | ||
| sample_size-1+ラグ数 len(データ)-1 | sample_size | ←検証期間の終期 |
プログラム
プログラムではグーグルドライブに上げたファイルから読み込むことにしています。
AutoRegの設定の中に、old_names=Faslseがあります。old_namesは係数名の表示の古い形式を表しますが、非推奨となっています。デフォルトではold_namesを使うことになっていますが、それを新形式にするようにしています。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.tsa.ar_model import AutoReg
from google.colab import drive
# ① Google Driveから読み込み
drive.mount('/content/drive', force_remount=True)
ci_df = pd.read_csv('/content/drive/MyDrive/MGDP/CI.csv')
ci = ci_df['ci'].values.astype(np.float32)
# ② パラメータ設定
n_lags = 2
sample_size = len(ci) - n_lags
train_size = int(sample_size * 0.9)
# ③ 学習データの作成(ラグを含める)
train_data = ci[:train_size + n_lags]
# ④ モデル学習
model = AutoReg(train_data, lags=n_lags, old_names=False).fit()
# ⑤ 推定値(実績期間):fittedvalues は n_lags 分遅れて始まる
ci_estimated = model.fittedvalues # 長さは len(train_data) - n_lags
# ⑥ 予測値(検証期間):train_size 以降を予測
ci_forecast = model.predict(start=train_size + n_lags, end=len(ci)-1)
# ⑦ 結果表示
print(model.summary())
print("推定された係数:", model.params)
# ⑧ グラフ表示
plt.figure(figsize=(14, 6))
plt.plot(ci, label="True", color='gray')
# 実績期間の推定値をプロット(x軸の対応に注意)
plt.plot(range(n_lags, train_size + n_lags), ci_estimated, label="Fitted (Estimation)", linestyle='--', color='blue')
# 検証期間の予測値をプロット
plt.plot(range(train_size + n_lags, len(ci)), ci_forecast, label="Forecast", linestyle='--', color='green')
plt.axvline(x=train_size + n_lags - 1, color='gray', linestyle=':') # 実績と予測の境界線
plt.legend()
plt.grid(True)
plt.title("AR Model: Estimation vs Forecast")
plt.show()