pythonで最小二乗法の計算をしてみます。statsmodelsというパッケージを使い、以下の式で計算できます。
sm.OLS(被説明変数,説明変数）
scikit-learnというパッケージでも最小二乗法は計算できます。まずモデルを指定して、fit関数で説明変数と被説明変数を指定します。
LinearRegression()
fit（説明変数,被説明変数）
経済統計の使い方では、経済統計の入手法から分析法まで解説しています。
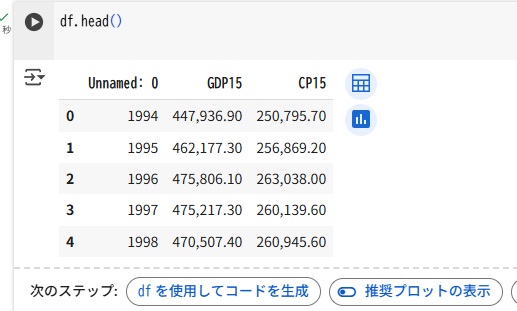
データは、以下のデータを使います。GDP（国内総生産）と消費のデータです。
import pandas as pd
df=pd.read_csv("cp.csv")
df.head()GDP15は実質GDP、CP15は実質民間最終消費で単位は10億円です。データの概要は以下の通りです。０列目は日付（年）のデータが入っています。
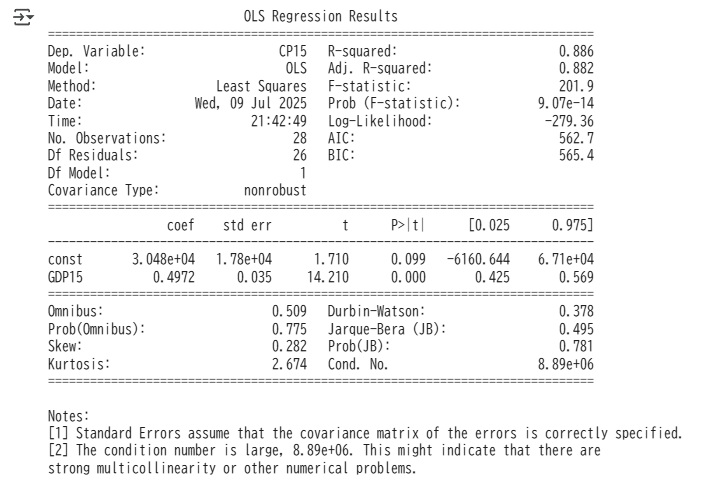
satatmodelsを使う場合（結果がわかりやすい）
最小二乗法で消費関数を分析する場合について説明します。定数項をa,GDP95の係数をbとして以下の式を推計します。
statsmodelsを使うと結果がわかりやすいです。最小二乗法の核となる式は以下です。
sm.OLS(被説明変数,説明変数）
sm.add_constantを使うことにより、定数項が付加されます。
import statsmodels.api as sm
y=df["CP15"]
X=df["GDP15"]
X=sm.add_constant(X)
model= sm.OLS(y,X)
results=model.fit()
print(results.summary())sm.OLS関数は数式を作りますが、実際の計算は、fitメソッドで行います。fitメソッドを使うと、回帰係数や残差の系列、様々な統計量が計算されます。
推計結果をresultsという変数に入れ、その概要をsummaryメソッドで作り、printコマンドで出力しています。
scikit-learnを使う場合（応用範囲が広い）
scikit-learnパッケージを使う場合です。結果の表示はstatmodelsの方がわかりやすいですが、機械学習などのほかの手法への応用範囲が広いです。
被説明変数はpandasのシリーズですが、被説明変数はデータフレーム（2次元）にする必要があります。df[“GDP15”]だとシリーズとして取り出すことになるので、データフレームとして取り出すためには、列名のリスト（一つだけのリスト）を指定するという意味で、df[[“GDP15”]]とします。
推定するモデルが最小二乗法の場合はLinearRegression()のクラス（設計図）を使います。回帰係数などの計算をするのが、fit()メソッドです。カッコ内に（説明変数、被説明変数）を入れます。statmodelsと説明変数と被説明変数の順番が逆で、説明変数、被説明変数の順です。statsmodelsパッケージでは定数項を付加する必要がありますが、scikit-learnパッケージでは定数項は自動的に付加されます。
LinearRegression()
fit（説明変数,被説明変数）
推定値を計算するのがpredictメソッドになります。
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score, mean_squared_error
y=df["CP15"]
X=df[["GDP15"]]
model = LinearRegression()
model.fit(X, y)
y_pred = model.predict(X)
print("回帰係数（weights）:", model.coef_)
print("切片（intercept）:", model.intercept_)
print("決定係数（R²）:", model.score(X, y))
print("平均二乗誤差 (MSE):", mean_squared_error(y, y_pred))出力
回帰係数（weights）: [0.49716147]
切片（intercept）: 30482.215282431105
決定係数（R²）: 0.8859338333346064
平均二乗誤差 (MSE): 27134718.252458863
- 【Python】テンソルの操作（Pytorch)
- 【python】深層学習の計算手順（学習と検証）(Pytorch)
- 【python】 最小二乗法の計算｜statsmodelsとscikit-learn
- 【python】とにかくどんなデータか知りたい
- 【python】行や列を加える（データフレーム）
