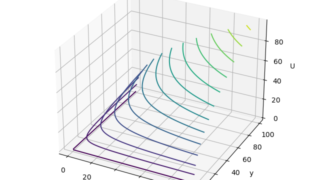
【経済学】限界効用が逓増する財はあるか？｜あったとして、無差別曲線はどうなる？

限界効用逓増

消費の理論では限界効用は逓減するとされています。購入量を一つ増やすと、追加的に効用がどのくらい増えるかを限界効用と呼び、購入量を増やすごとに限界効用が徐々に減っていく（逓減）する財が普通です。

ケーキも最初の1個はおいしいですが、2個目、3個目と食べていくと、限界効用は減っていくでしょう。

一方で、限界効用が逓増する財はないのでしょうか？検討してみます。

経済統計の使い方では、統計データの入手法から分析法まで解説しています。

【経済学】経済学のまとめ経済学の基本的な考え方について説明しました。経済統計の使い方では、統計データの入手法から分析法まで解説しています。 ...

Contents

限界効用が逓増する場合
両方の財が効用逓増の場合
プログラム
- 無差別曲線のプログラム
- 効用関数のプログラム

限界効用が逓増する場合

購入当初、限界効用が逓増する財はあります。

ある人にとっては、美術館がその例になるかもしれません。1回目に行った時はそれほど絵の良さがわからなかったけれど、通うにつれて絵の面白さがわかっていく場合です。限界効用は上がっていくでしょう。

また、自動車のミニチュアモデルなど、通信販売で部品が送られてきて、徐々に完成していく場合も、完成に近づけば近づくほど限界効用が上がるかもしれません。

ただ、さらに繰り返す場合はどうでしょうか。美術館の場合、ある程度の回数を超えるとやはり限界効用は逓減するかもしれません。自動車のミニチュアも、完成までは限界効用が逓増するかもしれませんが、それを何台も作っていくと限界効用が減少していくかもしれません。

ただ、とにかく集めるのが好きなコレクターだと、集めれば集めるほど、効用が上がる人もいるかもしれません…

両方の財が効用逓増の場合

両方の財が限界効用逓増の場合、

・ｘ財が少なく、y財が多い（限界効用大）時は、ｘ財を1単位増加したときｙ財の減少分は小さい
・ｘ財が多く、y財が少ない（限界効用小）時は、ｘ財を1単位増加した時のｙ財の減少分は大きい

x財が増えるにしたがって、傾きが急になっていくことがわかります。通常の財と反対です。

効用関数が $x^{2} + y^{2}$ の場合は以下のような無差別曲線になります。

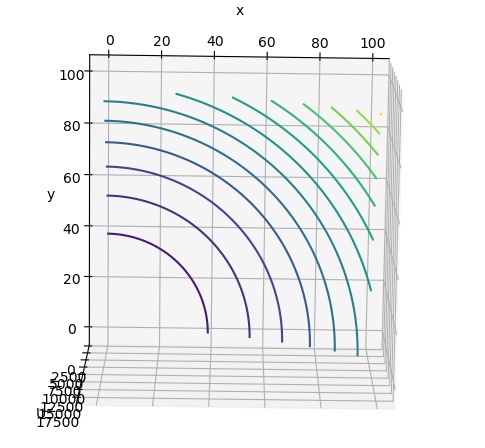
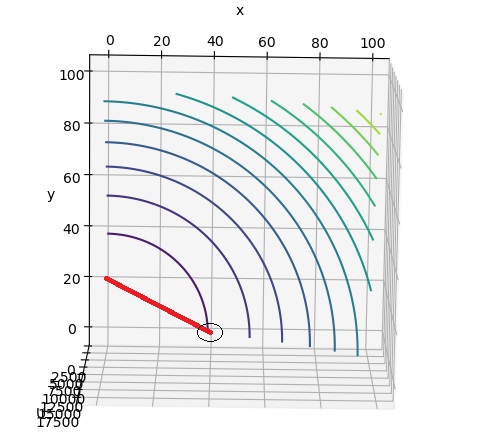
予算が40の時で、x財、y財の価格比が1:2の場合の予算線は下記のように引けます。効用が最大となるのは、x財のみを40単位買うということになります。

プログラム

無差別曲線のプログラム

#jupyter notebook 上でグラフを動かせるようにする
%matplotlib notebook

#matplotlib,Axes3D,numpy を使えるようにする。
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import numpy as np

 
#x（x財の購入量）,y（ｙ財の購入量）,z（効用） のデータを作成
#効用関数
def f(x, y):
    return x**2+y**2
#xとｙのデータ：0から99まで1刻み
x = np.arange(0, 100, 1)
y = np.arange(0, 100, 1)

#x,yのすべての組み合わせについて効用を計算する
x, y = np.meshgrid(x, y)

U = f(x, y)

#立体グラフの設定
fig = plt.figure()
ax = Axes3D(fig)

ax.set_xlabel("x")
ax.set_ylabel("y")
ax.set_zlabel("U")

#等高線グラフの作成
ax.contour(x, y, U, 15) 

#グラフの表示
plt.show()

効用関数のプログラム

#jupyter notebook 上でグラフを動かせるようにする
%matplotlib notebook

#matplotlib,Axes3D,numpy を使えるようにする。
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import numpy as np

 
#x（x財の購入量）,y（ｙ財の購入量）,z（効用） のデータを作成
#効用関数
def f(x, y):
    return x**2+y**2
#xとｙのデータ：0から99まで1刻み
x = np.arange(0, 100, 1)
y = np.arange(0, 100, 1)

#x,yのすべての組み合わせについて効用を計算する
x, y = np.meshgrid(x, y)

U = f(x, y)

#立体グラフの設定
fig = plt.figure()
ax = Axes3D(fig)

ax.set_xlabel("x")
ax.set_ylabel("y")
ax.set_zlabel("U")

#効用関数グラフの作成
ax.plot_wireframe(x, y, U)

#グラフの表示
plt.show()