変数の分布の形をみるには、まずヒストグラムを使い、代表値としては平均と分散を見ることが基本です。
さらにその系列の分布の特徴をみるには、尖度や歪度が使われます。
文字通り、歪度は分布の左右への歪み具合、尖度は尖り具合を表します。
経済統計の使い方では、統計データの入手法から分析法まで解説しています。

歪度ープラスだと左に偏る
歪度は以下の式で表されます。
$ 歪度=\dfrac{E[(X_t- \mu )^3]}{ \sigma^3}$
歪度は、分布がどの程度歪んでいるかを表します。歪度がプラスだと、分布が左側に偏っています。右側に歪んでおり、右裾が長いという表現もできますが、頂点は左側にあります。マイナスの場合は右側に偏っています。
座標軸で考えるとで正の数値は右、負の数値は左側にありますが、正の場合は左側に頂点があり、直感とは逆側に偏っていることになります。
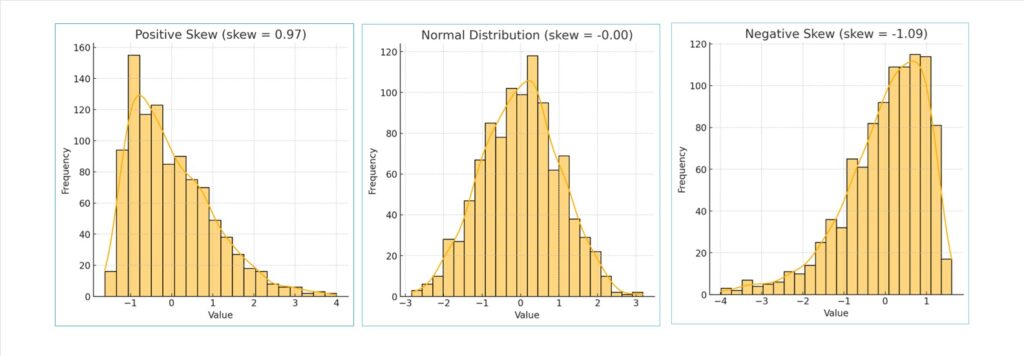
歪度は、データの分布の非対称性を示す指標であり、平均よりも大きい(右側の)データが多い場合、歪度は**正(プラス)になります。逆に、平均よりも小さい(左側の)データが多い場合、歪度は負(マイナス)**になります。
エクセルの関数では=SKEW(数値1,数値2,…)を使います。
SKEW(数値1,数値2,…)正規分布の時は0
エクセルの場合は、正規分布の時の歪度が0になるように調整されています。左に偏っているとプラス、右に偏っているとマイナスになります。
尖度ープラスだと尖っている
エクセルでは尖度は以下の式で表されます。
$ 尖度=\dfrac{E[(X_t- \mu )^4]}{ \sigma^4}-3 $
尖度は分布の形がどの程度と尖っているのかを表します。0より大きいと尖っており、0より小さいと平らになります。0の場合が正規分布になります。ばらつきを表す分散と似ていますが、さらに極端な値の集中を表します。
エクセルの関数では、=KURT(数値)を使います。
KURT(数値1,数値2,…)正規分布が3の場合も
エクセルの関数では、正規分布の時尖度が0になるように調整してありますが、3を引かずに以下の式で計算されたものを尖度とする場合もあります。この場合は正規分布の時3になります。この計算式が通常の尖度で、エクセルで出力される尖度は過剰尖度と呼ばれることがあります。
$ 尖度=\dfrac{E[(X_t- \mu )^4]}{ \sigma^4} $
正規分布とカイ二乗分布
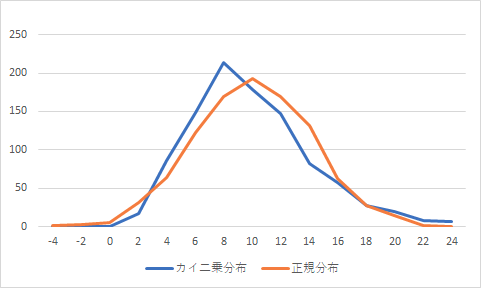
正規分布とカイ二乗分布について、平均、標準偏差、歪度、尖度を見てみましょう。乱数を発生させて、以下の数値を1000サンプル作り、ヒストグラムにしました。平均と標準偏差はほぼ同じになります。
- 正規分布:平均9、標準偏差4 =NORM.INV(RAND(),9,4)
- カイ二乗分布:自由度9 =CHISQ.INV(RAND(),9)
| 正規分布 | カイ二乗分布 | |
| 平均 | 9.1 | 9.0 |
| 標準偏差 | 4.0 | 4.3 |
| 歪度 | 0.0 | 0.9 |
| 尖度 | 0.0 | 1.3 |
モーメント
歪度や尖度を体系的に理解するにはモーメントを理解すると良いと思います。モーメントはもともと物理学の用語で、以下を表します。
ある点を中心として、回転させる能力の大きさ
式で書くと、点からの距離×力です。
統計学では、ある値からの距離の期待値がモーメントと定義されます。物理学と違って、距離は考えられていますが、力は一定と想定しています。ゼロの周りのモーメントは単にモーメント、平均値($\mu$)の周りのモーメントを中心モーメントと呼びます。$r$次のモーメントはモーメントをr乗したものです。$r$次の中心モーメントは以下のように表せます。
$ \mu_r=E[(X_t-\mu )^r]$
次に、モーメントを平均と標準偏差で標準化したものを標準化モーメントと呼びます。
$ \mu_r=E\left[\left(\dfrac{ X_t-\mu }{\sigma} \right)^r\right]=\dfrac{E[(X_t- \mu )^r]}{ \sigma^r} $
これらのモーメントと代表値との関係をみると以下のようになります。
| モーメント(ゼロの周り) | 中心モーメント(平均値の周り) | 標準化モーメント(平均値の周りで標準化) | |
| 1次 | 平均値 | ||
| 2次 | 分散 | ||
| 3次 | 歪度 | ||
| 4次 | 尖度 |
1次のモーメント
1次の原点からのモーメントは、$X_t$の期待値なので、平均になります。
$ \mu=E[X_t]$
2次のモーメント
2次の平均からのモーメントは分散です。
$ \mu_2=E[(X_t-\mu )^2]$
3次のモーメント
3次の標準化モーメントは歪度です。
$ 歪度=E\left[\left(\dfrac{X_t-\mu }{\sigma} \right)^3\right]=\dfrac{E[(X_t- \mu )^3]}{ \sigma^3}$
4次のモーメント
4次の標準化モーメントは尖度です。エクセルの場合はこれから3を引いたものを尖度としています。
$ 尖度=E\left[\left(\dfrac{X_t-\mu }{\sigma} \right)^4\right]=\dfrac{E[(X_t- \mu )^4]}{ \sigma^4}$
ジャック=ベラ検定
ジャック=ベラ検定は、正規分布しているかどうかの検定です。検定名は、考案者のCarlos JarqueとAnil K. Bera にちなんでつけられました。最初の論文はEfficient Tests for Normality, Homoscedasticity and Serial Independence of Regression Residuals です。
帰無仮説は「正規分布している」で、この仮説のもとで以下の検定統計量が自由度2のカイ二乗分布することが知られています。
$ JB=\dfrac{n}{6} \left[ S^2+0.25*(K)^2 \right] $
ここで、$n$はサンプル数、$S$は歪度、$K$はエクセルで計算した場合の尖度です。
上記の例では以下の結果となりました。カイ二乗分布の場合は、「正規分布である」という帰無仮説を棄却できます。
| 正規分布 | カイ二乗分布 | |
| ジャック=ベラ検定量 | 0.034457 | 2146551 |
| P値 | 0.982919 | 0.000000 |
まとめ
分布の特徴を表す代表値として平均、分散以外のものを紹介しました。
歪度は、分布が一方に歪んでいる度合いを表します。
尖度は、分布の尖り具合を表します。
歪度は3次の標準化モーメント、尖度は4次の標準化モーメントです。
ジャック=ベラ検定は、歪度と尖度を使った正規分布の検定です。